Пусть в некоторой области задано векторное поле
a = ax i + ay j + az k
и какая-либо двухсторонняя поверхность S. Разобьем поверхность каким-либо способом на элементарные площадки D Si. На каждой площадке выберем произвольную точку Pi и составим интегральную сумму:
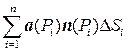 . (6.1)
. (6.1)
Если существует предел такой суммы при D Si ®0, то этот предел называется поверхностным интегралом 2-го рода и обозначается символом
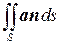 или
или 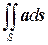 ,
,
где d s = n ds.
Поскольку единичный вектор нормали имеет своими координатами направляющиеся косинусы n ={cosa, cosb, cosg}, то
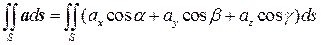 . (6.2)
. (6.2)
Этот интеграл представляет собой не что иное, как поверхностный интеграл
1-го рода. Таким образом, вычисление поверхностных интегралов 2-го рода можно свести к вычислению поверхностных интегралов 1-го рода. Однако, что в отличие от поверхностных интегралов 1-го рода интегралы 2-го рода зависят от выбора стороны поверхности. Переход к другой стороне поверхности меняет направление нормали к поверхности, а соответственно и знак интеграла.
Рассмотрим интеграл
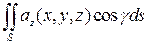 .
.
|
|
|
Пусть уравнение поверхности имеет вид z =j(x,y) и положительной стороной этой поверхности будем считать ту, нормаль которой образует с осью O z острый угол. Тогда
cosg ds = dxdy.
Поэтому рассматриваемый интеграл можно записать в виде
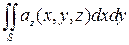 .
.
Заменяя z на j(x,y), придем к двойному интегралу
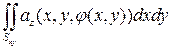 ,
,
где Sxy – проекция поверхности S на плоскость xOy.
Аналогично рассматриваются оставшиеся два интеграла. В результате, вычисление поверхностного интеграл 2-го рода сводится к вычислению трех двойных интегралов:
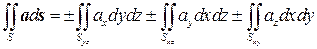 . (6.3)
. (6.3)
Знак "плюс" здесь выбирается в том случае, если интегрирование происходит по той стороне поверхности, которая обращена в сторону положительных направлений осей Ox, Oy и Oz. Если это не так, то нужно взять знак "минус" у соответствующего интеграла.
Замечание. Следует иметь в виду, что, поверхностные интегралы 2-го рода (в соответствии с формулой (6.3)) часто записывают в виде
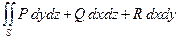 , (6.4)
, (6.4)
где P=P (x,y,z), Q=Q (x,y,z), R=R (x,y,z) – какие-то функции, заданные на поверхности S.
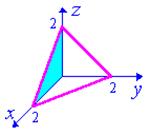
Пример 6.1. Вычислить поток векторного поля a = y j через верхнюю часть плоскости x+y+z =2, лежащей в первом октанте (см. рис. 6.3).
|
| Рис. 6.3 |
Решение. Поскольку ax =0, ay = y, az =0, то
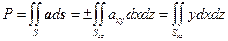 .
.
Так как уравнение плоскости имеет вид y =2 –x–z и нормаль к поверхности образует с осью Oy острый угол (это означает, что cosb>0 и поэтому перед интегралом нужно выбрать знак "+"), то
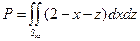 .
.
Далее, переходя к повторным интегралам, получим
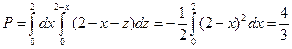 .
.
Пример 6.2. Вычислить поток векторного поля a = z k через внешнюю сторону сферы S: x 2 +y 2 +z 2=1.
Решение. Поскольку ax=ay =0, az=z, то
|
| Рис. 6.5 |
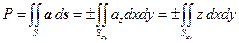 .
.
Здесь z нельзя выразить однозначной функцией от x и y для всей поверхности интегрирования. Разобьем поверхность на две части, верхнюю S' и нижнюю S'':
|
|
|
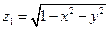 и
и 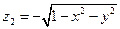 .
.
Тогда
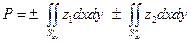 .
.
Перейдем к двойным интегралам. Так как S' – верхняя часть сферы, нормаль которой на всей полусфере образует с осью Oz острый угол, то
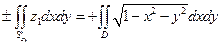 ,
,
где D – круг x 2+ y 2£1. S'' – нижняя часть сферы, нормаль которой на всей полусфере образует с осью Oz тупой угол, то
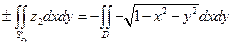 ,
,
где D – тот же круг. В результате получаем
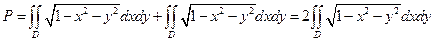 .
.
Перейдя в полярную систему координат, получим
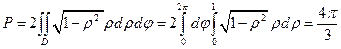 .
.
Вопрос. Чему равнялся бы поток, если бы a = z 2 k.
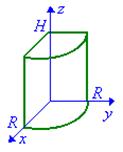
Пример 6.3. Вычислить поток векторного поля a =2 x i – y j через часть поверхности цилиндра S: x 2 +y 2= R 2, x ³0, y ³0, 0£ z £ H, в направлении внешней нормали (см. рис. 6.5).
Решение. Поскольку ax= 2 x, ay =– y, az= 0, то
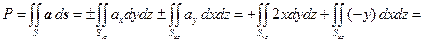
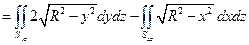 .
.
Поскольку Syz является прямоугольником размера R ´ H и Sxz – точно такой же прямоугольник, то оба интеграла в последнем выражении являются одинаковыми. Поэтому можно написать
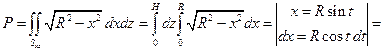
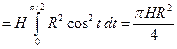 .
.
 2014-02-12
2014-02-12 1622
1622








