Теорема (Остроградского-Гаусса). Поток векторного поля a ( r ) через замкнутую поверхность S, находящуюся в этом поле, в направлении ее внешней нормали, равен тройному интегралу по области V, ограниченной этой поверхностью, от дивергенции этого векторного поля, т.е.
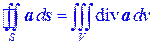 . (6.9)
. (6.9)
Доказательство. Пусть объем V, ограниченный поверхностью S, разбит на большое число малых объемов D vi, поверхности которых D si. Тогда, в соответствии с определением дивергенции, можно написать
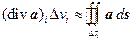 ,
,
где (div a) i означает значение дивергенции в какой-либо точке объема D vi. Просуммируем по всем этим малым объемам обе части приведенного равенства:
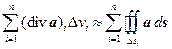 . (6.10)
. (6.10)
Левую часть равенства (6.9) при D vi ®0 можно выразить в виде тройного интеграла
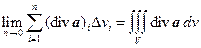 .
.
Преобразуем теперь правую часть выражения (6.10), но прежде отметим, что все внутренние ячейки рассматриваемого объема соприкасаются друг с другом. Тогда поток через поверхность соприкосновения будет входить в сумму дважды как поверхностные интегралы по соприкасающимся поверхностям соседних ячеек, причем эти интегралы будут равны, но противоположны по знаку. В результате, все интегралы по поверхностям внутри объема V дадут нуль. Следовательно, останется лишь сумма интегралов по внешней поверхности S:
|
|
|
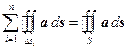 .
.
Таким образом, из выражения (6.10) получаем формулу Остроградского-Гаусса. &
Замечание. Формула (6.9) была получена М.В. Остроградским (1801-1861) в 1828 г. На западе эту формулу связывают только с именем К. Гаусса (1777-1855), однако им эта формула была получена в 1813 г. для одного частного случая, когда в тройном интеграле, входящем в эту формулу, подынтегральная функция равна 1, тогда как Остроградским эта формула была получена для функций любого числа переменных. Следует отдать должное Гауссу, поскольку формула (6.9) стала широко известна благодаря его исследованиям в области электростатики.
Формула Остроградского-Гаусса играет важную роль во многих приложениях векторного анализа и часто значительно облегчает вычисления потоков через замкнутые поверхности. Например, рассмотрим векторного поля a =yz i + xz j + xy k через какую-либо замкнутую поверхность. Поскольку div a =0, то, по формуле Остроградского-Гаусса, поток векторного поля a равен нулю, какова бы ни была форма замкнутой поверхности S.
Пример 6.5. Вычислить поток векторного поля
a = x 3 i + y 3 j + z 3 k
через сферу S: x 2+ y 2+ z 2= R 2.
Решение. Воспользовавшись формулой Остроградского-Гаусса, получим
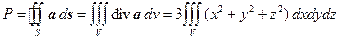 .
.
Откуда, вводя сферические координаты, получим
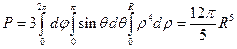 .
.
Пример 6.6. Вычислить поток векторного поля
a = x 3 i + y 3 j + R 2 z k
через поверхность S: 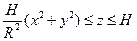 .
.
Решение. Поскольку div a =3(x 2+ y 2)+ R 2, то формуле Остроградского-Гаусса получаем
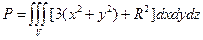
Перейдем к цилиндрическим координатам
|
|
|
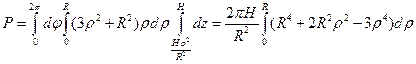
окончательно получаем
R = p HR 4.
 2014-02-12
2014-02-12 960
960







