Прямолинейно-параллельный фильтрационный поток упругой жидкости

Основная формула теории упругого режима

Точные решения уравнения пьезопроводности.

Одномерные фильтрационные потоки упругой жидкости.

Рассмотрим наиболее простые точные решения уравнения пьезопроводности (7.10) для одномерных потоков.

Случай 1. Приток к галерее, на которой поддерживается постоянное давление.

Пусть в полубесконечном горизонтальном пласте постоянной толщины h и ширины В начальное пластовое давление всюду постоянно и равно р_K. На галерее (при х = 0) давление мгновенно снижено до р_Г и в дальнейшем поддерживается постоянным (т.е. p_Г = const). В удаленных точках (х → ∞) давление в любой момент времени остается равным р.

В пласте образуется неустановившийся прямолинейно-параллельный поток упругой жидкости. Давление в любой точке потока х и в любой момент времени t можно определить, интегрируя уравнение пьезопроводности (7.10), которое для одномерного течения в декартовой системе координат запишется

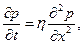0 < х < ∞. (7.12)

Начальные и граничные условия, сформулированные выше и записанные виде математических соотношений, будут следующие:

р(х,t)= p_к при t = 0;

р(x,t)= p_r при x = 0, t >0;

р(x,t) = p_к при х = ∞, t ≥ 0. (7.13)

Задача заключается в определении дебита галереи Q(t) и давления в любой точке потока и в любой момент времени p(x,t).

Используя анализ размерностей, покажем, что поставленная задача автомодельна, т.е. из аргументов, от которых зависит давление, можно составить один безразмерный комплекс, от которого будет зависеть искомая функция p(x,t).

Обозначим через P = (p-p_r)/(p_к-р_r) безразмерное давление, которое, как следует из соотношений (7.12) и (7.13), зависит от времени t, координаты х и коэффициента пьезопроводности η, т.е.

P = f(x, t, η).

Размерности этих аргументов следующие: длина [ x ] = L, время [t] = T, [η] = L²T^-1, и из них можно составить безразмерный комплекс 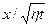или переменную безразмерную величину 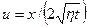. Задача сводится к нахождению безразмерного давления Р зависящего от u (автомодельной переменной): P = f(u) с граничными условиями

Р = 0 при u = 0; P = 1 при u = ∞. (7.14)

В силу линейности дифференциального уравнения (7.12) для безразмерного давления Р имеем такое же уравнение, как и для размерного р

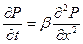(7.15)

Используя правило дифференцирования сложных функций, частные производные по координате и времени выражают через производные по безразмерной (автомодельной) производной, затем подставляют граничные условия (7.14) в (7.15), интегрируют и получают закон распределения давления в неустановившемся прямолинейно-параллельном фильтрационном потоке упругой жидкости (вывод Басниев 2005 стр. 199, 1993 стр. 140)

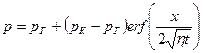(7.16)

Типичные кривые распределения давления в различные моменты времени в неустановившемся прямолинейно-параллельном потоке упругой жидкости в галерее, пушенной в эксплуатацию с постоянным забойным давлением р_г = const, приведены на рис. 5.1.

Дебит галереи Q считаем положительным, отбираемый из галереи (х = 0), когда поток движется против оси х.

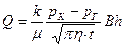(7.17)

Из формулы (7.17) следует, что дебит галереи убывает с течением времени как 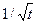и при t → ∞ стремится к нулю. В начальный момент времени t = 0 формула (7.17) дает бесконечное значение дебита, что является следствием скачка давления на галерее (от р_К до р_г).

Накопленная к моменту t добыча V_доб (объем добытой нефти) определяется по формуле:

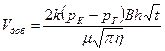(7.18)

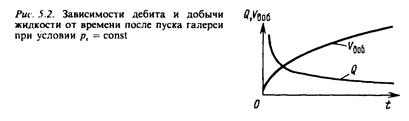
Т.е. сразу после начала отбора из галереи она быстро возрастает, а в дальнейшем растет очень медленно (рис. 5.2).

Случай 2. Приток к галерее, на которой поддерживается постоянный дебит.

В таком же полубесконечном пласте, что и в случае 1, в момент времени t = О пущена в эксплуатацию галерея с постоянным объемным дебитом Q. Требуется найти давление в любой точке пласта в любой момент времени. Математически задача заключается в интегрировании уравнения (7.15) при следующих начальных и граничных условиях:

р(х, t) = р_К при t = 0;

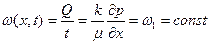при x = 0, t >0;

р(x,t) = p_к при х → ∞, t > 0. (7.19)

Первое условие, как и в первом случае, задает распределение давления в пласте до пуска в галерее, и из него следует, что давление во всех точках пласта постоянно и равно контурному. Второе условие задает постоянство дебита на галерее после ее пуска. Из третьего условия следует, что граница возмущенной зоны с ростом времени перемещается к бесконечности. (вывод Басниев 2005 стр. 202, 1993 стр. 143)

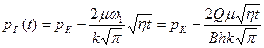(7.20)

Решение (7.20) при очень больших значениях теряет физический смысл. Полученный результат означает, что принятое граничное условие 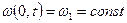является слишком «жестким», для его реализации требуются отрицательные значения давления при большом времени. Реально эти давления возникать не будут - возникнет кавитация вблизи галереи.