Согласно теореме Карно, КПД тепловой машины не может превышать КПД обратимой машины, работающей между теми же температурами: η≤ηобр.. По определению, КПД всякой тепловой машины η=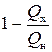 ,
,
где Q н – теплота, полученная машиной от нагревателя, при температуре Т н,
Q х – теплота, отданная машиной холодильнику при температуре Т х.
Максимально же возможный КПД, т.е. КПД обратимой машины, работающей между теми же температурами, 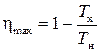 . Таким образом,
. Таким образом,
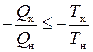 . (6)
. (6)
Здесь как получаемая теплота Q н>0, так и отдаваемая теплота Q х>0.
Однако далее везде вместо терминов «получаемая теплота» и «отдаваемая теплота» удобно пользоваться единым термином: «теплота, которой система обменивается с тепловыми резервуарами», причём получаемой теплоте приписывать знак «+», а отдаваемой – «−»: Q >0, когда система получает теплоту, и Q <0, когда отдаёт (т.е. получает отрицательную теплоту). Таким образом, система получает теплоту всегда, но только с разными знаками.
В этом случае соотношение (6) принимает вид:
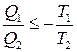 , (7)
, (7)
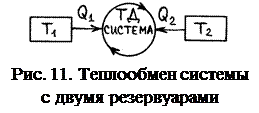
где Q 1=− Q х – теплота, которой система обменивается с резервуаром при температуре Т 1, Q 2= Q н – теплота, которой система обменивается с резервуаром при температуре Т 2 (рис. 11).
Замечание. При теплообмене с каким-либо резервуаром температура системы должна быть равна температуре данного резервуара, − это обязательное условие обратимости процесса. Теплового контакта двух тел с разными температурами в обратимых процессах быть не должно.
Из (7) следует, что для двух резервуаров с температурами Т 1 и Т 2, с которыми система обменивается теплотами Q 1 и Q 2, справедливо неравенство:
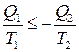 ,
,
или: 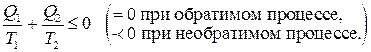 (8)
(8)
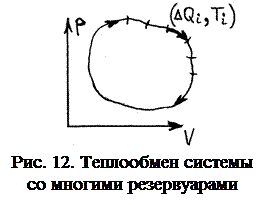 Однако в круговом процессе система может обмениваться теплотами Δ Qi не обязательно с двумя, а со многими резервуарами с разными температурами Ti (рис. 12). При этом справедлива следующая теорема (без доказательства):
Однако в круговом процессе система может обмениваться теплотами Δ Qi не обязательно с двумя, а со многими резервуарами с разными температурами Ti (рис. 12). При этом справедлива следующая теорема (без доказательства):
Теорема. Если есть п тепловых резервуаров с температурами Т 1, Т 2, …, Тп, с которыми система в круговом процессе обменивается теплотами Δ Q 1, Δ Q 2, …, Δ Qп, то справедливо соотношение, аналогичное (8):
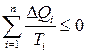 (=0 при обратимом процессе). (9)
(=0 при обратимом процессе). (9)
Если же источники тепла (резервуары) распределены непрерывно, и каждый из них обменивается с системой теплотой dQ при соответствующей температуре Т, то вместо суммы (9) следует писать интеграл по циклу:
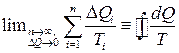 ,
,
и тогда 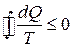 . (10)
. (10)
Это фундаментальное термодинамическое соотношение, вытекающее из второго закона ТД, называется неравенством Клаузиуса. Для обратимых циклов
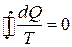 . (11)
. (11)
 Замечание. Так как при обратимом теплообмене с каким-либо резервуаром температура системы обязательно должна быть равна температуре данного резервуара, то в выражениях (10) и (11) в качестве Т следует брать температуру самóй системы.
Замечание. Так как при обратимом теплообмене с каким-либо резервуаром температура системы обязательно должна быть равна температуре данного резервуара, то в выражениях (10) и (11) в качестве Т следует брать температуру самóй системы.
Определение. Пусть в элементарном процессе теплообмена система получает теплоту dQ при температуре Т. Тогда отношение 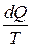 называется элементарной приведённой теплотой системы, а интеграл
называется элементарной приведённой теплотой системы, а интеграл 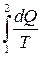 − приведённой теплотой системы в конечном процессе 1-2 (рис. 13).
− приведённой теплотой системы в конечном процессе 1-2 (рис. 13).
С учётом этого, равенство (11) можно сформулировать следующим образом:
приведённая теплота системы при любом обратимом циклическом процессе равна нулю.
Следствия из равенства (11):
Следствие 1. КПД любого обратимого цикла, в котором минимальная температура равна Т 1, а максимальная − Т 2, меньше, чем КПД цикла Карно, работающего между теми же температурами: η<ηКарно (без доказательства).
Следствие 2. Приведённая теплота системы при обратимом переходе из одного состояния в другое не зависит от формы пути перехода, а определяется только начальным и конечным состояниями системы.
 Доказательство. Пусть L 1 и L 2 – два различных обратимых (квазистатических) процесса, переводящих систему из состояния 1 в 2 (рис. 14). Рассмотрим циклический процесс 1→ L 1→2→ L 2→1. Для этого обратимого цикла справедливо равенство (11), которое можно представить как сумму процессов:
Доказательство. Пусть L 1 и L 2 – два различных обратимых (квазистатических) процесса, переводящих систему из состояния 1 в 2 (рис. 14). Рассмотрим циклический процесс 1→ L 1→2→ L 2→1. Для этого обратимого цикла справедливо равенство (11), которое можно представить как сумму процессов:
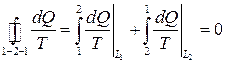 .
.
Но 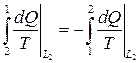 , следовательно,
, следовательно, 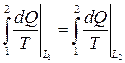 .
.
 2014-02-12
2014-02-12 1862
1862








