Последовательные приближения корней

i	x	y	z
	0,5	0,5	0,5
	0,875	0,5	0,375
	0,78981	0,49662	0,36993
	0,78521	0,49662	0,36992

Останавливаясь на приближении x ⁽³⁾, будем иметь:

x = 0,7852; y = 0,4966; z =0,3699.

Мы получили систему линейных уравнений, неизвестными в которой выступают величины 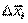. Решив ее, например, методом Гаусса, мы получим некое новое приближение к 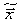, т.е. 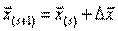. Выражение (3) можно представить как обобщение на систему уравнений итерационного метода Ньютона, рассмотренного в предыдущей главе:

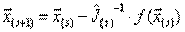, (4)

где в данном случае

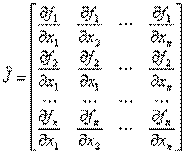– матрица Якоби, которая считается для каждого (s) приближения.

Критерием окончания итерационного процесса является условие 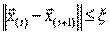(Можем принять под 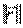как норму 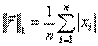, так и 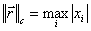). Достоинством метода является высокая скорость сходимости. Сходимость метода зависит от выбора начального приближения: если 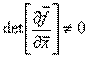, то итерации сходятся к корню. Недостатком метода является вычислительная сложность: на каждой итерации требуется находить матрицу частных производных и решать систему линейных уравнений. Кроме того, если аналитический вид частных производных неизвестен, их надо считать численными методами.

Метод простых итераций.

Метод простых итераций для решения (1) аналогичен методу, рассмотренному при решении нелинейных уравнений с одним неизвестным. Прежде всего, выбирается начальное приближение 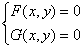, а исходная система уравнений преобразуется к эквивалентной системе вида

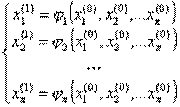, (5)

и по ней осуществляется итерационный цикл. Если итерации сходятся, то они сходятся к решению уравнения (1). Обозначим 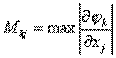. Достаточным условием сходимости является 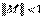. Скорость сходимости метода сильно зависит от вида конкретно подбираемых функций 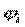, которые должны одновременно удовлетворять условиям эквивалентности (5) и (1), и обеспечивать сходимость итерационного процесса.

Например, для исходной системы уравнений 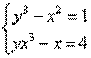эквивалентная итерационная система (5) может быть представлена в следующем виде:

,

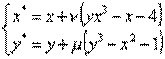где множители 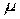= –0.15 и 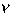= –0.1 подбираются из анализа условий сходимости.

Листинг программы решения системы 2 х 2 (Паскаль)

uses crt;

var

d,e,x1,x2,y1,y2:real;

c,k,p:integer;

ch:char;

function f1(x1,x2:real):real;

begin

f1:=x1*sin(x1)-x2;

end;

function f2(x1,x2:real):real;

begin

f2:=x1*x1+x2*x2-1;

end;

procedure fun_y1_1_y2;

begin

y1:= x1-f1(x1,x2)/2+f2(x1,x2)/8;

y2:= x2+f1(y1,x2)/2-f2(x1,x2)/2;

end;

procedure fun_y1_y2;

begin

y1:= x1-f1(x1,x2)/2+f2(x1,x2)/8;

y2:= x2+f1(x1,x2)/2-f2(x1,x2)/2;

end;

procedure outputofresult;

begin

clrscr;

writeln('Korni uravnenia:');

writeln('x1 = ', y1:1:5);

writeln('x2 = ', y2:1:5);

writeln('Pogreshnosty priblegenia = ', d:1:7);

writeln;

writeln('Kolichestwo iteraziy = ',k);

writeln('Dlia prodolgenia nagmite lubui klavishu...');

repeat ch:= readkey until ch <> '';

k:=k+1;

end;

begin

repeat

k:=0; e:=0.001;

clrscr;

writeln('Reshenie sistem nelineinyh uravneni');

writeln('');

writeln('1 - Metod prostoiq iterazy');

writeln('2 - Metod Zeydely');

writeln('0 - Exit');

writeln('');

write('Enter: ');

readln(p);

c:=0;

if p=1 then c:=1;

if p=2 then c:=2;

if p=0 then c:=0;

case c of

0:begin

exit;

end;

1:begin

writeln('Vvedite nachalnoe priblegenie:');

write('x1 = ');

readln(x1);

write('x2 = ');

readln(x2);

repeat

fun_y1_y2;

d:= abs(y1-x1);

if abs(y2-x2)>d then d:= abs(y2-x2);

outputofresult;

x1:= y1; x2:= y2;

until d<e;

end;

2:begin

writeln('Vvedite nachalnoe priblegenie:');

write('x1 = ');

readln(x1);

write('x2 = ');

readln(x2);

repeat

fun_y1_1_y2;

d:= abs(y1-x1);

if abs(y2-x2)>d then d:= abs(y2-x2);

outputofresult;

x1:= y1; x2:= y2;

until d<e;

end;

end;

until (p<1) or (p>2);

end.

Решение контрольного примера

Метод простой итерации:

Начальное приближение

x1 = 0.9

x2 = 0.6

Корни уравнения

x1 = 0.80992

x2 = 0.58662

Погрешность приближения = 0.0006517

Количество итераций = 4

Метод Зейделя:

Начальное приближение

x1 = 0.9

x2 = 0.6

Корни уравнения

x1 = 0.80928

x2 = 0.58648

Погрешность приближения = 0.0006042

Количество итераций =11

Проверка:

0.80928*sin(0.80928) - 0.58648 0

(0.58648)² + (0.80928)² -1 0