Пример 1. Эскалатор поднимает идущего по нему вверх человека за t1 =1 мин. Если человек будет идти вдвое быстрее, то он поднимется за t2 =45 с. Сколько времени будет подниматься человек, стоящий на эскалаторе?
Решение. Пусть искомое время равно  t; расстояние, которое человек проезжает на эскалаторе, равно s, а скорость движения эскалатора равна v. При равномерном движении эти величины связаны соотношением
t; расстояние, которое человек проезжает на эскалаторе, равно s, а скорость движения эскалатора равна v. При равномерном движении эти величины связаны соотношением
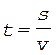 . (1)
. (1)
Аналогичные соотношения могут быть записаны для t 1 и t 2:
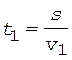 , (2)
, (2)
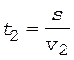 . (3)
. (3)
Скорости v 1 и v 2 можно найти следующим образом:
v 1 = v + v о, (4)
v 2 = v + 2 v о, (5)
где v 0 - скорость движения человека относительно эскалатора в случае, когда время подъема равно t 1.
Подставляя соотношения (4) и (5) в формулы (2) и (3), получим
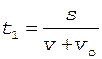 , (6)
, (6)
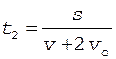 . (7)
. (7)
Перепишем соотношения (6) и (7) в виде
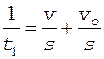 ,
,
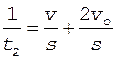 .
.
Введем обозначение x = v о /s. Тогда с учетом соотношения (1) получим систему уравнений
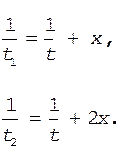


Почленное вычитание уравнения (8) из уравнения (9) дает
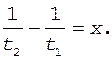
Подставляя x в уравнение (8), получим
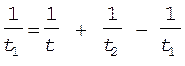 .
.
После преобразований получим выражение
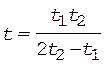 .
.
Выразив t 1 в секундах, находим
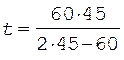 = 90 с.
= 90 с.
Пример 2. Скорость тела, движущегося прямолинейно, меняется по закону v = At + Bt 3, где A = 1 м/с2; B = 3 м/с4.
Чему будет равно ускорение тела к моменту времени, когда оно пройдет расстояние s = 14 м?
Решение. Ускорение есть производная от скорости по времени:
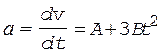 . (1)
. (1)
Время t находим, используя соотношение
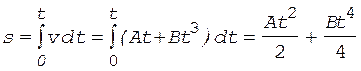 . (2)
. (2)
Введем обозначение z = t 2 и, используя исходные данные, запишем соотношение (2) в виде
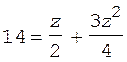 .
.
После преобразований получим уравнение
3 z 2 + 2 z - 56 = 0. (3)
Решение уравнения (3) дает
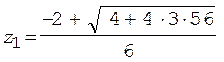 = 4 с2,
= 4 с2,
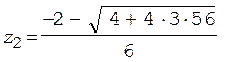 = -4,7 с2.
= -4,7 с2.
Значение z 2 должно быть отброшено, так как в соответствии с введенным обозначением z > 0. Подставляя z = 4 с2 в уравнение (1), находим
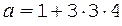 = 37 м/с2.
= 37 м/с2.
Пример 3. Траектория движения материальной точки задается уравнениями: x = At 2; y = Bt, где A = 4 м/с2; B = 2 м/с. Радиус кривизны траектории через промежуток времени t = 1 с после начала движения равен R = 17 м. Определить полное ускорение точки в этот момент времени. Построить траекторию движения за первые две секунды.
Решение. Уравнение траектории задано в параметрическом виде:
x = At 2, (1)
y = Bt. (2)
Чтобы получить уравнение траектории в явном виде, исключим время из уравнений (1) и (2):
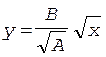 .
.
Полученное выражение представляет собой уравнение верхней ветви параболы, ось которой направлена вдоль оси x. Для построения траектории найдем по уравнениям (1) и (2) значения x и y в моменты времени, взятые с интервалом 0,5 с:
| t, c | x, м | y,м |
| 0,0 | ||
| 0,5 | ||
| 1,0 | ||
| 1,5 | ||
| 2,0 |
Траектория движения точки представлена на рис. 1.
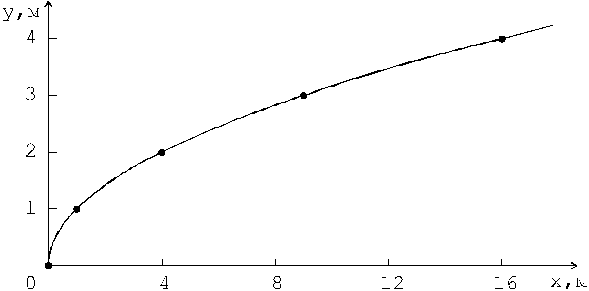 |
Рис. 1
Полное ускорение определяется по формуле
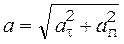 , (3)
, (3)
где 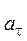 и
и 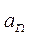 - тангенциальное и нормальное ускорения соответственно. Эти ускорения находим по формулам
- тангенциальное и нормальное ускорения соответственно. Эти ускорения находим по формулам
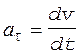 , (4)
, (4)
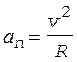 , (5)
, (5)
где v - модуль вектора скорости точки, определяемый по формуле
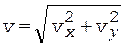 . (6)
. (6)
В свою очередь, vx и vy - проекции вектора скорости на оси x и y - вычисляются по формулам
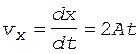 , (7)
, (7)
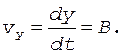 (8)
(8)
Подставляя уравнения (7) и (8) в (6), получим
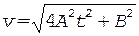 , (9)
, (9)
а затем в соответствии с формулой (4) находим
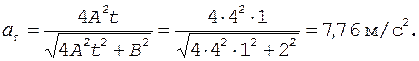 (10)
(10)
Вычисления по формуле (9) дают значение модуля скорости, равное v = 8,25 м/с, что после подстановки в уравнение (5) позволяет определить нормальное ускорение:
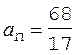 = 4 м/с2. (11)
= 4 м/с2. (11)
Подставляя результаты вычислений по формулам (10) и (11) в выражение (4), находим полное ускорение:
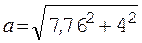 = 8,73 м/с2.
= 8,73 м/с2.
Пример 4. Шайба лежит на платформе, вращающейся вокруг вертикальной оси. Расстояние от шайбы до оси вращения равно R = 2 м. При частоте вращения n = 9 об/мин шайба начинает скользить по платформе. Определить коэффициент трения шайбы о платформу.
Решение. На шайбу действуют три силы (рис. 2): сила тяжести 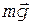 , сила нормальной реакции опоры
, сила нормальной реакции опоры 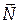 и сила трения
и сила трения 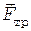 .
.
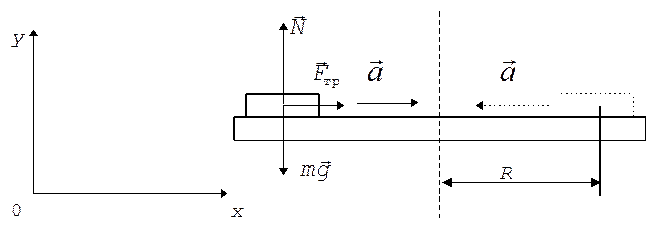
Рис.2
Запишем уравнение движения шайбы (второй закон Ньютона) сначала в векторной форме:
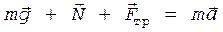 ,
,
затем в проекциях на оси O x:
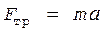 (1)
(1)
и O y:
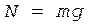 . (2)
. (2)
Оставаясь неподвижной относительно платформы, шайба вместе с тем движется с ускорением, которое является центростремительным и определяется по формуле
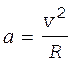 , (3)
, (3)
где v - линейная скорость шайбы.
Модуль силы трения вычисляется по формуле
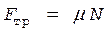 , (4)
, (4)
где m - коэффициент трения.
Перепишем формулу (4) с учетом уравнения (2):
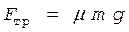 , (5)
, (5)
а уравнение (1) - с учетом формул (3) и (5):
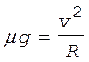 . (6)
. (6)
Линейная скорость связана с частотой вращения соотношением
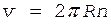 . (7)
. (7)
Подставляя уравнение (7) в формулу (6), имеем
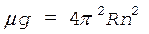 .
.
После преобразований и подстановки исходных данных в системе СИ получим
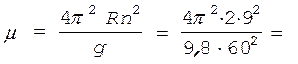 0,18.
0,18.
Пример 5. Конькобежец массой m 1, стоя на льду, толкает в горизонтальном направлении камень массой m 2 = 5 кг и откатывается назад со скоростью u 1= 0,3 м/с относительно земли. Коэффициент трения камня о лед равен m =0,06; расстояние, на которое переместился камень, равно s = 15 м. Определить массу конькобежца.
Решение. Конькобежец и камень (рис. 3) составляют замкнутую систему, для которой выполняется закон сохранения импульса
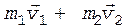
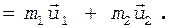 (1)
(1)
Левая часть уравнения (1) представляет собой импульс системы "конькобежец - камень" до толчка, когда камень и конькобежец покоились; правая — после толчка.

Рис. 3
Запишем уравнение (1) в проекциях на горизонтальную ось:
0 = - m 1 u 1 + m 2 u 2
и получим выражение для модуля скорости камня после броска
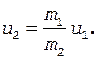 (2)
(2)
При движении камня по льду на него действуют три силы: сила тяжести 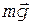 , сила нормальной реакции опоры
, сила нормальной реакции опоры 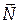 и сила трения
и сила трения 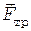 . Первые две силы перпендикулярны к направлению движения и работы не совершают, поэтому работа всех сил будет равна работе силы трения:
. Первые две силы перпендикулярны к направлению движения и работы не совершают, поэтому работа всех сил будет равна работе силы трения:
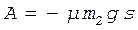 .
.
Изменение кинетической энергии камня в процессе торможения после броска составит
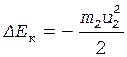 .
.
Используя теорему о кинетической энергии, получим
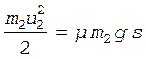 . (3)
. (3)
Переписав формулу (3) с учетом выражения (2):
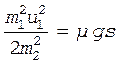 ,
,
получим выражение для расчета искомой величины
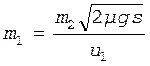 .
.
После подстановки исходных данных имеем
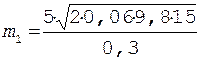 = 70 кг.
= 70 кг.
Пример 6. Нерастяжимая тонкая гибкая нить одним концом закреплена, как показано на рис.4, затем перекинута через невесомый подвижный блок и через неподвижный блок в виде сплошного диска массой m = 6 кг. К подвижному блоку подвешен груз массой m 1 = 5 кг, ко второму концу нити подвешен груз массой m 2 = 10 кг.
Определить: 1) скорости поступательного движения грузов v 1 и v 2 , когда они, будучи предоставленными самим себе, придут в движение и правый груз опустится на высоту h = 3,5 м; 2) ускорения a 1 и a 2, с которыми будут двигаться грузы; 3) силы натяжения нити. Трением, массой нити и массой подвижного блока можно пренебречь.
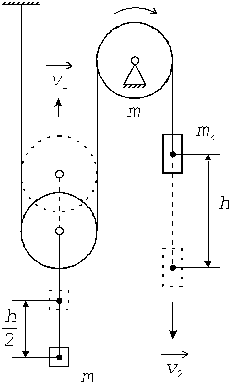 Рис. 4
Рис. 4
| 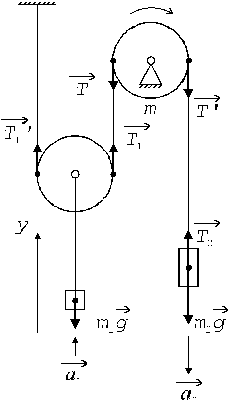 Рис. 5
Рис. 5
|
Решение. На тела системы действуют консервативные силы тяжести и упругости, поэтому выполняется закон сохранения механической энергии:
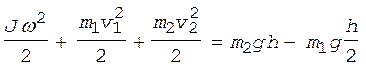 , (1)
, (1)
где w - угловая скорость неподвижного блока;
J - момент инерции неподвижного блока.
Очевидно, что
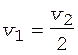 . (2)
. (2)
Скорость поступательного движения правого груза совпадает с линейной скоростью точек, лежащих на ободе неподвижного блока, поэтому
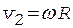 , (3)
, (3)
где R - радиус неподвижного блока.
Момент инерции блока в виде сплошного диска определяется по формуле
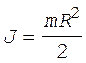 . (4)
. (4)
Перепишем уравнение (1) с учетом формул (2)-(4):
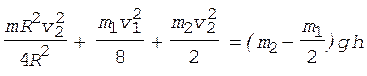 .
.
После преобразований получим
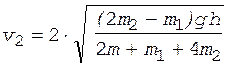 . (5)
. (5)
Подставляя исходные данные в формулу (5), найдем скорость v 2:
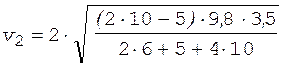 = 6 м/с,
= 6 м/с,
а затем по формуле (2) вычислим v 1:
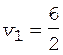 = 3 м/с.
= 3 м/с.
Ускорение второго груза найдем по формуле
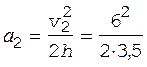 = 5,14 м/с2. (6)
= 5,14 м/с2. (6)
Очевидно, что ускорение первого груза будет вдвое меньше:
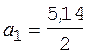 = 2,57 м/с2. (7)
= 2,57 м/с2. (7)
Рассмотрим силы, действующие на тела системы (рис. 5). На первый груз действуют силы натяжения нити  и
и  , а также сила тяжести
, а также сила тяжести 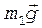 . На второй груз действует сила тяжести
. На второй груз действует сила тяжести 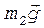 и сила натяжения нити
и сила натяжения нити 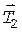 .
.
Направим ось y вертикально вверх и напишем для каждого груза уравнение движения (второй закон Ньютона) в проекциях на эту ось.
Для первого груза
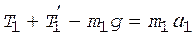 , (8)
, (8)
для второго груза
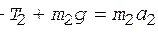 . (9)
. (9)
Момент сил 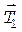 и
и 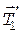 относительно оси подвижного блока равен нулю, так как блок невесомый. Из этого следует, что
относительно оси подвижного блока равен нулю, так как блок невесомый. Из этого следует, что 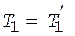 и уравнение (8) может быть переписано в виде
и уравнение (8) может быть переписано в виде
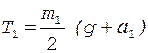 .
.
Найдем Т 1 с учетом формулы (7):
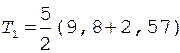 = 30,9 Н. (10)
= 30,9 Н. (10)
Выразим T 2 из уравнения (9) и найдем с учетом (6):
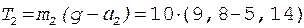 = 46,6 H. (11)
= 46,6 H. (11)
Под действием сил 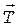 и
и 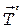 неподвижный блок будет вращаться по часовой стрелке с угловым ускорением e. Согласно основному закону динамики вращательного движения
неподвижный блок будет вращаться по часовой стрелке с угловым ускорением e. Согласно основному закону динамики вращательного движения
T'R - TR = Je. (12)
Угловое ускорение e связано с ускорением второго груза а 2 и радиусом неподвижного блока R соотношением
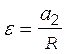 . (13)
. (13)
Подстановка формул (4) и (13) в выражение (12) приводит после сокращения на R к уравнению
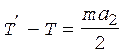 .
.
Это уравнение нужно лишь для проверки правильности ранее найденных значений Т 1 и Т 2, так как согласно третьему закону Ньютона с учетом невесомости нити имеем
T' = Т 2 = 46,6 Н,
Т = Т 1 = 30,9 Н.
Пример 7. Горизонтальная платформа в виде сплошного диска массой m 1 = 200 кг вращается вокруг вертикальной оси, проходящей через ее центр, с частотой n = 8,5 об/мин. Человек массой m 2 стоит при этом в центре платформы. Когда человек перешел на край платформы, она стала вращаться с частотой n ’ = 5 об/мин. Найти массу человека, считая его материальной точкой.
Решение. Человек и платформа представляют собой замкнутую систему тел, вращающихся вокруг одной и той же неподвижной оси. Для такой системы справедлив закон сохранения момента импульса
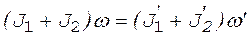 , (1)
, (1)
где J 1 и 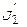 — моменты инерции платформы до и после перехода человека соответственно;
— моменты инерции платформы до и после перехода человека соответственно;
J 2 и 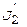 — моменты инерции человека до и после перехода соответственно;
— моменты инерции человека до и после перехода соответственно;
w — угловая скорость платформы и человека до перехода;
w ’ — угловая скорость платформы и человека после перехода.
Угловые скорости связаны с частотой вращения соотношениями
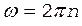 , (2)
, (2)
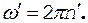 (3)
(3)
Момент инерции платформы (сплошного диска) определяется по формуле
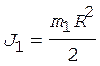 , (4)
, (4)
где R - радиус платформы.
Очевидно, что J 1 = 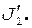 Момент инерции человека (материальной точки), находящегося на краю платформы, определяется по формуле
Момент инерции человека (материальной точки), находящегося на краю платформы, определяется по формуле
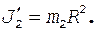 (5)
(5)
Момент инерции человека, стоящего в центре платформы, равен J 2 = 0. C учетом этого, а также принимая во внимание формулы (2)-(5), перепишем уравнение (1) в виде
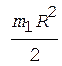
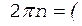
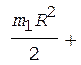
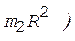
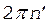 .
.
После сокращений на общие множители и перегруппировки членов получим
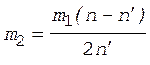 . (6)
. (6)
Подстановка исходных данных в формулу (6) дает
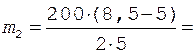 70 кг.
70 кг.
 2015-01-30
2015-01-30 565
565








