Понятие производной

Пусть в промежутке [ a; b ] задана непрерывная функция 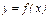и пусть 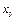- точка в этом промежутке.

1. Дадим значению аргумента 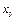приращение 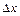; получим точку 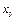+ 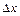, также принадлежащую этому промежутку. Найдем значения функции в точках 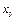и + .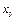

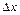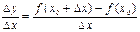2. Составим приращение функции – приращение функции есть разность значений функции в конечной и начальной точках.

3. Находим отношение приращения функции к приращению аргумента

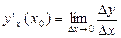Если существует конечный предел отношения приращения функции к приращению аргумента при стремлении приращения аргумента к нулю, то он называется производной функции 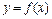в точке :

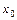Если этот предел существует, то существует и производная в данной точке 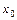, и функция называется дифференцируемой в данной точке. Функция называется дифференцируемой в промежутке, если она дифференцируема в каждой точке этого промежутка. Если функция дифференцируема в точке, то она и непрерывна в этой точке. Но из непрерывности функции в точке не следует дифференцируемость (существование производной) в точке. Поэтому при применении производной в конкретной задаче необходимо учитывать область определения, как самой функции, так и ее производной.

Геометрический смысл производной состоит в том, что значение производной функции в точке 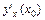есть угловой коэффициент касательной, проведенной к графику функции в данной точке.