Определения. Пусть a, b – действительные числа, i – некоторый символ. Комплексным числом называется запись вида a + bi.
Сложение и умножение чисел на множестве комплексных чисел: (a + bi) + (c + di) = (a + c) + (b + d)i,
(a + bi)(c + di) = (ac – bd) + (ad + bc)i..
Теорема 1. Множество комплексных чисел С с операциями сложения и умножения образует поле. Свойства сложения
1) Коммутативност ь: (a + bi) + (c + di) = (a + c) + (b + d)i = (c + di) + (a + bi).
2) Ассоциативность: [(a + bi) + (c + di)] + (e + fi) = (a + c + e) + (b + d + f)i = (a + bi) + [(c + di) + (e + fi)].
3) Существование нейтрального элемента: (a + bi) + (0 + 0i) = (a + bi). Число 0 + 0 i будем называть нулём и обозначать 0.
4) Существование противоположного элемента: (a + bi) + ( – a – bi) = 0 + 0i = 0.
5) Коммутативность умножения: (a + bi)(c + di) = (ac – bd) + (bc + ad)i = (c + di)(a + bi).
6) Ассоциативность умножения:если z1 = a + bi, z2 = c + di, z3 = e + fi, то (z1z2)z3 = z1(z2z3).
7) Дистрибутивность: если z1 = a + bi, z2 = c + di, z3 = e + fi, то z1(z2 + z3) = z1z2 + z1z3.
8) Нейтральный элемент для умножения: (a + bi)(1 + 0i) = (a·1 – b·0) + (a·0 + b·1)i = a + bi.
9) Число 1 + 0i = 1 – единица.
9) Существование обратного элемента: " z ¹ 0 $z – 1 : zz – 1 = 1.
Пусть z = a + bi. Действительные числа a, называют действительной, а b - мнимой частями комплексного числа z. Используются обозначения: a = Rez, b = Imz.
Если b = 0, то z = a + 0i = a – действительное число. Поэтому множество действительных чисел R является частью множества комплексных чисел C: R Í C.
Заметим: i2 = (0 + 1i)(0 + 1i) =– 1 + 0i =– 1. Используя это свойство числа i, а также свойства операций, доказанные в теореме 1, можно выполнять действия с комплексными числами по обычным правилам, заменяя i2 на – 1.
Замечание. Отношения £, ³ («меньше», «больше») для комплексных чисел не определяются.
2 Тригонометрическая форма записи.
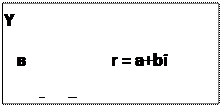


 Запись z = a+bi называется алгебраической формой записи комплексного числа. Рассмотрим плоскость с выбранной декартовой системой координат. Будем изображать число z точкой с координатами (a, b). Тогда действительные числа a = a + 0i будут изображаться точками оси OX – она называется действительной осью. Ось OY называется мнимой осью, её точки соответствуют числам вида bi, которые иногда называют чисто мнимыми. Вся плоскость называется комплексной плоскостью. Число
Запись z = a+bi называется алгебраической формой записи комплексного числа. Рассмотрим плоскость с выбранной декартовой системой координат. Будем изображать число z точкой с координатами (a, b). Тогда действительные числа a = a + 0i будут изображаться точками оси OX – она называется действительной осью. Ось OY называется мнимой осью, её точки соответствуют числам вида bi, которые иногда называют чисто мнимыми. Вся плоскость называется комплексной плоскостью. Число 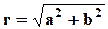 называется модулем числа z:
называется модулем числа z: 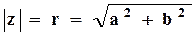 ,
,
Полярный угол j называется аргументом числа z:  j = argz.
j = argz.
Аргумент определяется с точностью до слагаемого 2kp; значение, для которого – p < j £ p, называется главным значением аргумента. Числа r, j являются полярными координатами точки z. Ясно, что a = r·cosj, b = r·sinj, и мы получаем: z = a + b·i = r·(cosj + i ·sinj). тригонометрической форма записи комплексного числа.
Сопряжённые числа. Комплексное число 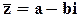 называется сопряжённым числу z = a + bi. Ясно, что
называется сопряжённым числу z = a + bi. Ясно, что 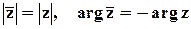 . Свойства:
. Свойства: 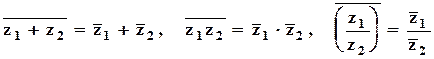 .
.
Замечание. Сумма и произведение сопряжённых чисел есть числа действительные:
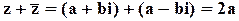 ,
, 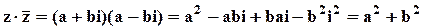 .
.
 2015-01-30
2015-01-30 4240
4240
