2015-05-13
5580
ПОСЛЕДОВАТЕЛЬНОСТИ КОМПЛЕКСНЫХ ЧИСЕЛ
Под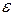 
-окрестностью точки 
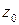будем понимать внутренность круга радиуса 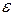с центром в точке 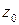, то есть множество точек 
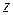, для которых 
.
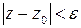Определение. Число 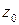называется пределом последовательности комплексных чисел 
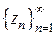, если 
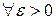можно указать такой номер 
, 
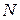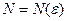, начиная с которого выполняется неравенство 
.
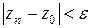Иначе: если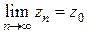 
, то как бы мала ни была 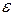-окрестность точки 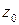, все точки последовательности 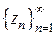, начиная с 
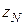, попадут внутрь этой окрестности. Существование предела 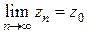равносильно существованию двух пределов:
, 
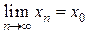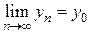, где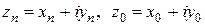 
.
Пример 1. Найти 1)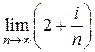 
; 2)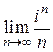 
.
Решение. 1) Имеем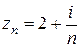 
, значит 
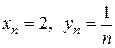. Из существования пределов 
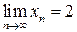и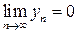 
следует, что предел последовательности 
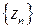существует и равен 
.
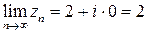2) Представим число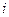 
в тригонометрической форме: 
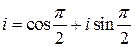. Затем применим формулу Муавра
.
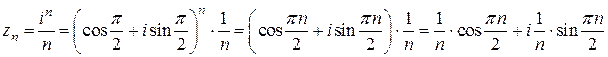Значит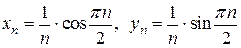 
. Из существования пределов 
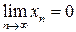и 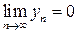(произведение ограниченной последовательности на бесконечно малую последовательность) следует, что предел последовательности 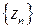существует и равен 
. ☻
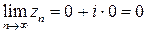Определение. Последовательность комплексных чисел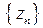 
называется ограниченной, если существует такое число 
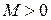, что для всех элементов 
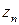последовательности имеет место неравенство 
(и неограниченной в противном случае).
Принято считать, что всякая неограниченно возрастающая последовательность комплексных чисел сходится к комплексному числу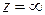 
. Комплексная плоскость вместе с бесконечно удаленной точкой, изображающей число 
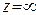, называется полной комплексной плоскостью. Точки неограниченно возрастающей последовательности комплексных чисел стремятся к точке 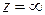независимо от направ-
ления на полной комплексной плоскости. Выражение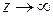 
означает 
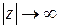, при этом аргумент бесконечно удаленной точки не имеет определенного значения (так же, как и аргумент точки 
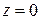). Окрестность бесконечно удаленной точки – это внешность круга с центром в точке 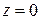, т.е. 
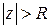. Для бесконечно удаленной точки устанавливаются следующие соотношения:
; 
; 
; 
.
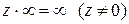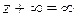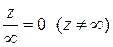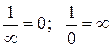Рассмотрим ряд с комплексными членами
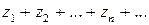(1)
Его частичные суммы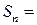 
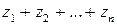. Ряд (1) называется сходящимся, если существует предел последовательности 
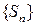частичных сумм при 
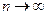. Этот предел 
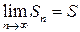называется суммой ряда.
Так как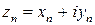 
, то сходимость ряда (1) равносильна сходимости двух рядов с действительными членам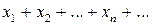и 
и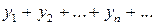 
.
Ряд (1) сходится тогда и только тогда, когда 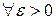можно указать такой номер 
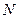, что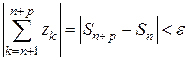 
при всех 
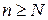и любом натуральном 
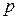(критерий Коши).
Пример 2. Показать, что необходимым условием сходимости ряда (1) является требование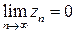 
.
Решение. Пусть ряд (1) сходится. В силу критерия Коши для 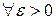можно указать такой номер 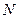, что при всех 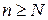и при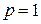 
: 
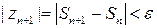. Это и означает, что последовательность 
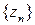бесконечно малая. ☻
Задача 1. Убедиться, что ряд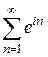 
расходится.
Если сходится ряд
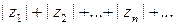, (2)
то сходится и ряд (1), который в этом случае называется абсолютно сходящимся.
Достаточные признаки сходимости ряда (2).
Признак Даламбера. Ряд (2) сходится, если выполняется соотношение
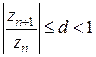для всех 
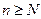, здесь 
.
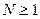Признак Коши. Ряд (2) сходится, если выполняется соотношение
для всех , .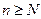
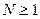Пример 3. Исследовать на сходимость ряд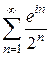 
.
Решение. По формуле Эйлера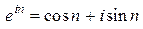 
. Таким образом, вопрос о
сходимости данного ряда сводится к вопросу о сходимости рядов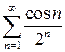 
и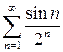 
. Для первого ряда 
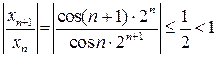. По признаку Даламбера этот ряд сходится абсолютно. Это верно и для второго ряда, значит, данный ряд сходится абсолютно. ☻
