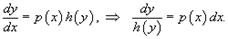
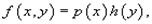
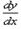 Дифференциальное уравнение первого порядка y' = f(x,y) называется уравнением с разделяющимися переменными, если функцию f(x,y) можно представить в виде произведения двух функций, зависящих только от x и y: где p(x) и h(y) − непрерывные функции. Рассматривая производную y' как отношение дифференциалов, перенесем d x в правую часть и разделим уравнение на h(y):
Дифференциальное уравнение первого порядка y' = f(x,y) называется уравнением с разделяющимися переменными, если функцию f(x,y) можно представить в виде произведения двух функций, зависящих только от x и y: где p(x) и h(y) − непрерывные функции. Рассматривая производную y' как отношение дифференциалов, перенесем d x в правую часть и разделим уравнение на h(y):
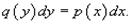
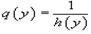 Если найдется число x0, при котором h(x0) = 0, то это число будет также являться решением дифференциального уравнения. Деление на h(y) приводит к потере указанного решения.
Если найдется число x0, при котором h(x0) = 0, то это число будет также являться решением дифференциального уравнения. Деление на h(y) приводит к потере указанного решения.
Обозначив, запишем уравнение в форме:
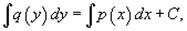 Теперь переменные разделены и мы можем проинтегрировать дифференциальное уравнение:
Теперь переменные разделены и мы можем проинтегрировать дифференциальное уравнение:
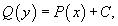 где C − постоянная интегрирования. Вычисляя интегралы, получаем выражение общее решение уравнения с разделяющимися переменными.
где C − постоянная интегрирования. Вычисляя интегралы, получаем выражение общее решение уравнения с разделяющимися переменными.
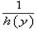 Замечания 1) Почленное деления ДУ на h(y) может привести к потере некоторых решений. Поэтому следует отдельно решить уравнение =0 и установить те решения ДУ, которые не могут быть получены из общего уравнения – особые решения.
Замечания 1) Почленное деления ДУ на h(y) может привести к потере некоторых решений. Поэтому следует отдельно решить уравнение =0 и установить те решения ДУ, которые не могут быть получены из общего уравнения – особые решения.
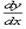 2) Уравнение y' = f1(x) · f2(y) также сводится к уравнению с разделяющими переменными. Для этого достаточно положить y' = и разделить переменные.
2) Уравнение y' = f1(x) · f2(y) также сводится к уравнению с разделяющими переменными. Для этого достаточно положить y' = и разделить переменные.
3) Уравнение y' = f(аx + вy +с), где а, в, с – числа. Путём замены u = аx + вy +с, сводится к ДУ с разделяющими переменными. Дифференцируя по х, получаем,
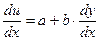 , т.е
, т.е 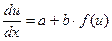 , откуда следует
, откуда следует 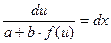
Интегрируя это уравнение и заменяя u на аx + вy +с, получим общий интеграл исходного уравнения
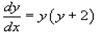
Пример 1 Решить дифференциальное уравнение.
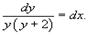 Решение. В данном случае p(x) = 1 и h(y) = y(y +2). Разделим уравнение на h(y) и перенесем dx в правую часть:
Решение. В данном случае p(x) = 1 и h(y) = y(y +2). Разделим уравнение на h(y) и перенесем dx в правую часть:
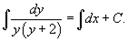
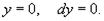 Заметим, что при делении мы могли потерять решения y = 0 и y = −2 в случае когда h(y) равно нулю. Действительно, убедимся, что y = 0 является решением данного дифференциального уравнения. Пусть Подставляя это в уравнение, получаем: 0 = 0. Следовательно, y = 0 будет являться одним из решений. Аналогично можно проверить, что y = −2 также является решением уравнения. Вернемся обратно к дифференциальному уравнению и проинтегрируем его:
Заметим, что при делении мы могли потерять решения y = 0 и y = −2 в случае когда h(y) равно нулю. Действительно, убедимся, что y = 0 является решением данного дифференциального уравнения. Пусть Подставляя это в уравнение, получаем: 0 = 0. Следовательно, y = 0 будет являться одним из решений. Аналогично можно проверить, что y = −2 также является решением уравнения. Вернемся обратно к дифференциальному уравнению и проинтегрируем его:
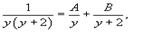
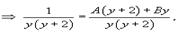
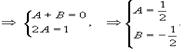
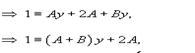 Интеграл в левой части можно вычислить методом неопределенных коэффициентов:
Интеграл в левой части можно вычислить методом неопределенных коэффициентов:
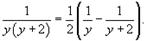
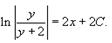
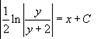 Таким образом, мы получаем следующее разложение рациональной дроби в подыинтегральном выражении: Следовательно,
Таким образом, мы получаем следующее разложение рациональной дроби в подыинтегральном выражении: Следовательно,
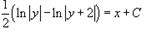
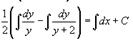
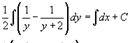
Переименуем константу: 2C = C1. В итоге, окончательное решение уравнения записывается в виде:
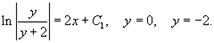
Общее решение здесь выражено в неявном виде. В данном примере мы можем преобразовать его и получить ответ в явной форме в виде функции y = f(x,C1), где C1 − некоторая константа. Однако это можно сделать не для всех дифференциальных уравнений.
Однородные дифференциальное уравнения. Функция f(x,y) называется однородной функцией n –го порядка, если при умножении каждого её аргумента на произвольный множитель λ вся функция умножиться λ n, т.е. f( λ· x, λ· y) = λ n· f(x,y)
Дифференциальное уравнение первого порядка y' = f(x,y) называется однородным, если функцию f(x,y) – есть однородная функция нулевого порядка.
Однородное уравнение преобразуется в уравнение с разделяющими переменными при помощи замены переменной (подстановки) 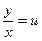 или, что, тоже самое,
или, что, тоже самое, 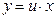
Решить дифференциальное уравнение 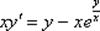
Функцию «игрек» необходимо заменить произведением некоторой функции (тоже зависящей от «икс») и «икса». Подставляем 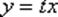 и
и 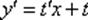 в исходное уравнение
в исходное уравнение 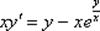
После подстановки проводим максимальные упрощения уравнения: 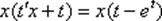 ;
; 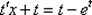 ;
; 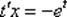 Далее алгоритм работает решения уравнения с разделяющимися переменными.
Далее алгоритм работает решения уравнения с разделяющимися переменными.
Если  – это функция, зависящая от «икс», то.
– это функция, зависящая от «икс», то. 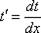 Таким образом:
Таким образом: 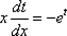
Разделяем переменные, при этом в левой части нужно собрать только «тэ», а в правой части – только «иксы»: 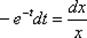 Переменные разделены, интегрируем:
Переменные разделены, интегрируем: 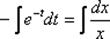
Получаем, 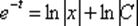
После того, как уравнение проинтегрировано, нужно провести обратную замену, она тоже стандартна и единственна: Если 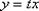 , то
, то 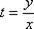 В данном случае:
В данном случае: 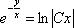 Чаще всего решение однородного уравнения записывают в виде общего интеграла.
Чаще всего решение однородного уравнения записывают в виде общего интеграла.
Ответ: общий интеграл: 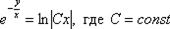
 2015-01-30
2015-01-30 2575
2575








