Інформаційна ситуація I4 характеризується невідомим розподілом
Р = (р1,..., рn), pj = P{θ = θj}, 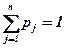 на елементах Θ, з одного боку, та відсутністю активної протидії середовища цілям щодо прийняття рішень суб'єктом керування з іншого. Поводження «пасивної природи», що досліджується у теорії статистичних рішень, та середовища співпадає. Інакше, ситуація I4 характеризується цілковитим незнанням суб'єктом керування про те, що стосується ймовірності поводження середовища.
на елементах Θ, з одного боку, та відсутністю активної протидії середовища цілям щодо прийняття рішень суб'єктом керування з іншого. Поводження «пасивної природи», що досліджується у теорії статистичних рішень, та середовища співпадає. Інакше, ситуація I4 характеризується цілковитим незнанням суб'єктом керування про те, що стосується ймовірності поводження середовища.
На практиці такі ситуації виникають, коли впроваджуються на підприємствах зразки нової техніки, коли мова йде про реалізацію нових зразків товарів народного споживання, коли зовсім невідомий попит, а також при відпрацюванні у виробництві нових технологічних способів, транспортних маршрутів тощо.
5.4.1. КРИТЕРІЙ БЕРНУЛЛІ-ЛАПЛАСА
В основу цього критерію покладено відомий «принцип недостатніх підстав». Він вперше був сформульований Бернуллі i в загальних рисах означає: якщо немає даних для того, щоб вважати один стан середовища з множини Θ більш імовірним, ніж будь-який інший стан середовища з множини Θ, то апріорні ймовірності рj станів середовища треба вважати рівними, тобто згідно з принципом недостатніх підстав точкові оцінки визначаються так
|
|
|
pj = 1/n, j = 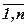 . (5.19)
. (5.19)
Ці оцінки розподілу апріорних імовірностей дозволяють застосовувати критерії першої інформаційної ситуації I1.
Критерій Бернуллі-Лапласа, що ґрунтується на застосуванні, критерію Байєса та принципу недостатніх підстав для одержання оцінок апріорних ймовірностей pj, формулюється таким чином.
Оптимальним згідно з критерієм Бернуллі-Лапласа є те рішення 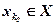 , котре задовольняє умову:
, котре задовольняє умову:
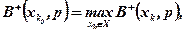
де
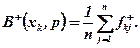 (5.20)
(5.20)
Таким чином, можливі стани розглядаються як рівно ймовірні, якщо немає жодних відомостей про умови, за яких кожний стан може відбутися.
Домінування розв'язку xk над розв'язком xi можна гарантувати у тому і лише в тому випадку, коли
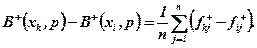 (5.21)
(5.21)
Тому необхідною та достатньою умовою пріоритету розв'язку xk з множини X є виконання нерівності
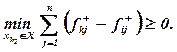 (5.22)
(5.22)
Пример. Пусть Х = {x1, x2, x3}, θ = {θ1, …, θ5} и задана матрица функционала оценивания:
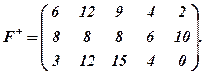
Решение. Согласно с критерием Бернулли – Лапласа получим, что р1 = р2 = р3 = р4 = р5 = 1/5, В+ (х1, р) = 33/5, В+ (х2, р) = 40/5; В+ (х3, р) = 34/5.
Следовательно, развязка «х2» является оптимальным, причём развязка «х3» лучше, чем «х1».
5.4.2. ПРИНЦИП МАКСИМУМУ ГIББСА-ДЖЕЙНСА
Згідно з принципом Гiббса-Джейнса найбільш характерними розподілами імовірностей станів невизначеного середовища є такі розподіли, котрі максимізують вибрану міру невизначеності при заданій інформації щодо поводження середовища.
|
|
|
Тут використовують формалізм відтворення невідомих законів розподілу випадкової величини за наявності обмежень з умов максимуму ентропії Шеннона
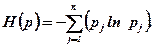 (5.23)
(5.23)
Необхідно зазначити, що Н(р) являє собою міру невизначеності, що знаходиться з розподілу апріорних імовірностей „ р” станів середовища.
Ентропія Шеннона є широко відомою мірою невизначеності та задовольняє таким властивостям (аксіомам):
1) Н(р) непрерывно дифференцированная по р 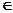 Δn, тут Δn – плоская множена:
Δn, тут Δn – плоская множена:
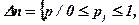
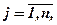
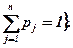
2) Н(р) ≤ 0 для р 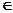 Δn и Н(р) = 0 для выраженного распределения;
Δn и Н(р) = 0 для выраженного распределения;
3) Н(р) унимодальная по р 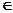 Δn, причём максимум Н(р) на Δn достигается при условии, что:
Δn, причём максимум Н(р) на Δn достигается при условии, что:
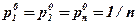 ;
;
4) Н(р0) = ln n – монотонно растёт при увеличении «n»;
5) Н(р) симметрична относительно р0 по р 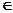 Δn;
Δn;
6) Н(р) согнута по р 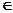 Δn;
Δn;
7) Н(р) аддитивна на положениях θj 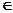 Θ.
Θ.
Формалізм Джейнса постулює: найменш сумнівним розподілом імовірностей буде такий, що максимізує невизначеність при врахуванні всієї заданої інформації.
Застосування принципу максимальної невизначеності Гiббса-Джейнса за умов інформаційної ситуації I4 дозволяє визначити точкову оцінку з умов
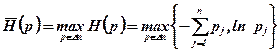 (5.24)
(5.24)
у видi рj = 1/n, j = 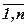 . Однако точковая оценка априорного распределения станів середовища постулюється також принципом Бернуллі-Лапласа.
. Однако точковая оценка априорного распределения станів середовища постулюється також принципом Бернуллі-Лапласа.
Суттєвою перевагою принципу максимальної невизначеності Гiббса-Джейнса є те, що існує можливість одержання оцінок апріорного розподілу, в яких суб'єктом керування можуть бути накладені обмеження на розподіл апріорних імовірностей станів середовища, наприклад, у формі завдання середніх та дисперсій (ризику) характеристик значень функціоналу оцінювання F.
Розглядають деякі з основних обмежень. Обмеження першого типу на байєсівські значення функціоналу оцінювання можуть бути такими
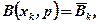
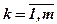 , (5.25)
, (5.25)
де за 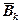 -може бути обрана, наприклад, оцінка середнього значення функціоналу оцінювання для розв'язку xk.
-може бути обрана, наприклад, оцінка середнього значення функціоналу оцінювання для розв'язку xk.
Обмеження першого типу на дисперсію значень функціоналу оцінювання можуть бути такими:
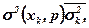
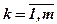 , (5.26)
, (5.26)
де 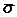 k2 - отже бути обрана, наприклад, величина ризику, як оцінка дисперсії значень функціоналу оцінювання для розв'язку xk
k2 - отже бути обрана, наприклад, величина ризику, як оцінка дисперсії значень функціоналу оцінювання для розв'язку xk 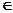 X:
X:
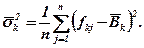 (5.27)
(5.27)
Аналогічно можуть вибиратися обмеження на моменти більш високого порядку як у формі рівнянь, так і нерівностей. Наприклад, для обмежень другого типу можна розглядати такі нерівності:
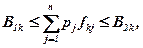
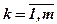 . (5.28)
. (5.28)
Одним із способів завдання В1k та В2k можуть бути використані межі довірчого інтервалу Bk. Аналогічні нерівності можуть бути введені і для врахування характеристик, що пов'язані з обмеженнями на допустимий ризик (врахування дисперсійних характеристик значень функціоналу оцінювання).
З математичної точки зору обмеження у вигляді рівнянь та нерівностей при використанні принципу максимальної невизначеності призводить до необхідності розв'язку задач опуклого математичного програмування. Для врахування обмежень у формі рівнянь можна використовувати апарат теорії коефіцієнтів Лагранжа. Для врахування обмежень у формі нерівностей використовують спеціальні методи, наприклад, метод занурення, узагальнені методи множників Лагранжа тощо.
У [50] формулюється ряд задач по знаходженню оцінки „ р” апріорного розподілу ймовірностей станів середовища на базі принципу Гіббса-Джейнса.
Задача 1. Визначити точкову оцінку " р" апріорного розподілу з умов:
 |

Пiсля того як визначені значення множників Лагранжа λ0 та λk, 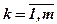 можна обчислити „ pj”, тобто розподіл ймовірностей, що обумовлює найбільше значення ентропії при заданих обмеженнях на середнє (сподіване) значення функціоналу оцінювання.
можна обчислити „ pj”, тобто розподіл ймовірностей, що обумовлює найбільше значення ентропії при заданих обмеженнях на середнє (сподіване) значення функціоналу оцінювання.
Для разв 'язання задачі 2 побудуємо функцію Лагранжа
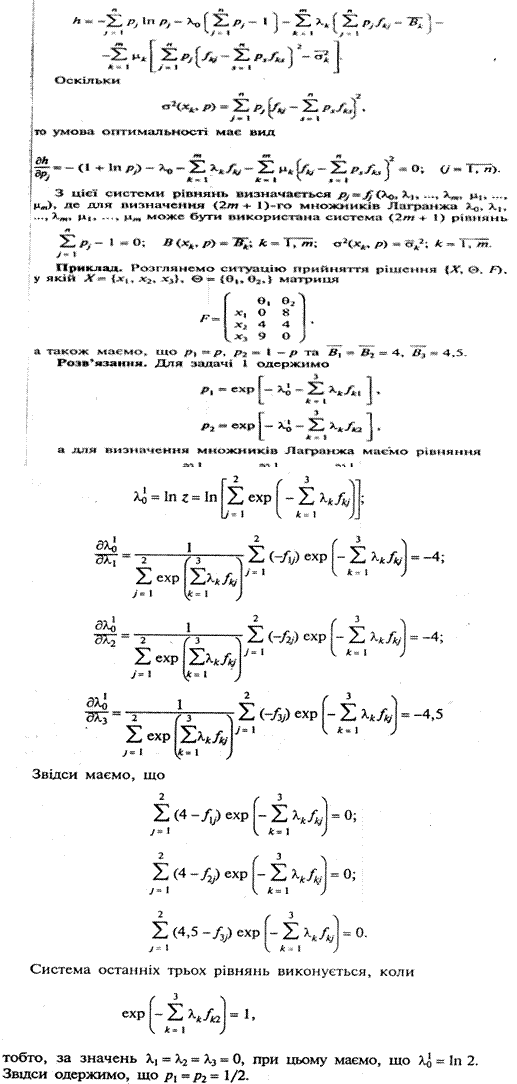
Тобто, в даному випадку ми маємо результат, що співпадає з принципом Бернуллі-Лапласа.
 2015-01-30
2015-01-30 466
466








