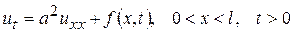 , (113)
, (113)
с начальными условиями
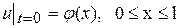 , (114)
, (114)
и граничными условиями
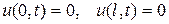 . (115)
. (115)
Решение этой задачи будем искать в виде ряда Фурье по системе собственных функций (94)
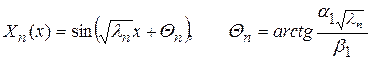 ,
,
т.е. в форме разложения
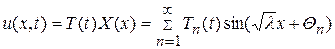 , (116)
, (116)
считая при этом t параметром.
Пусть функции f(x,t) является непрерывной и имеет кусочно-непрерывную производную 1-го порядка по х и при всех t >0 выполняются условия
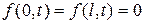 .
.
Предположим теперь, что функции f(x,t) и 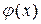 можно разложить в ряд Фурье по синусам
можно разложить в ряд Фурье по синусам
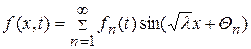 , (117)
, (117)
где
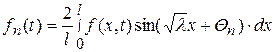 (118)
(118)
и
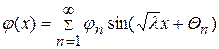 , (119)
, (119)
где
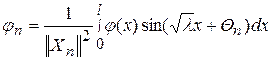 . (120)
. (120)
Подставим (116) в уравнение (113) и с учетом (117), получим
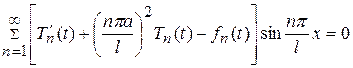 .
.
Это равенство выполняется тогда, когда
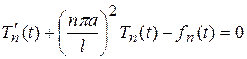 , (121)
, (121)
или, если 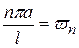 , то это уравнение (121) можно записать в виде
, то это уравнение (121) можно записать в виде
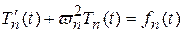 . (122)
. (122)
Пользуясь начальным условием (114) с учетом (116), (117) и (119) получаем, что
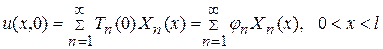 ,
,
откуда
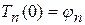 . (123)
. (123)
Таким образом, для нахождения искомой функции 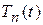 приходим к задаче Коши (122), (123) для обыкновенного неоднородного дифференциального уравнения первого порядка. Пользуясь формулой Эйлера можно записать общее решение уравнения (122)
приходим к задаче Коши (122), (123) для обыкновенного неоднородного дифференциального уравнения первого порядка. Пользуясь формулой Эйлера можно записать общее решение уравнения (122)
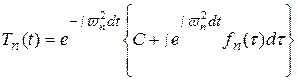 ,
,
а с учетом (123) решение задачи Коши
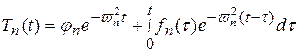 .
.
Следовательно, когда мы подставим значение этой функции в выражение (116), в итоге получим решение исходной задачи
|
|
|

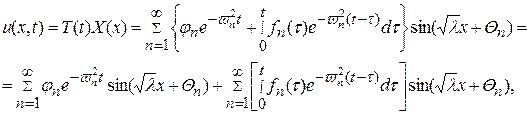 (124)
(124)
где функции f(x,t) и 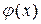 определены формулами (118) и (120).
определены формулами (118) и (120).
Пример 14. Найти решение неоднородного уравнения параболического типа
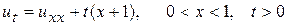 (14.1)
(14.1)
при начальном условии
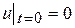 (14.2)
(14.2)
и граничных условиях
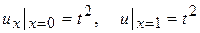 . (14.3)
. (14.3)
▲ Подберем сначала такую функцию v, чтобы удовлетворяла граничным условиям (14.3). Пусть, например, v = xt 2. Тогда
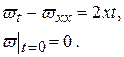
Следовательно, функция определяемая как
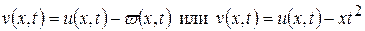 (14.4)
(14.4)
удовлетворяет уравнению
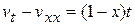 (14.5)
(14.5)
однородным граничным условиям
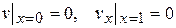 (14.6)
(14.6)
и нулевым начальным условиям
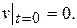 . (14.7)
. (14.7)
Применяя метод Фурье для решения однородного уравнения
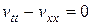
при условиях (14.6), (14.7), положим
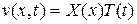 .
.
Приходим к следующей задаче Штурма-Лиувилля:
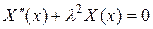 ,
, 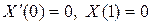 .
.
Решая эту задачу, находим собственные значения
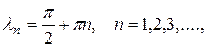
и соответствующие им собственные функции
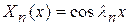 . (14.8)
. (14.8)
Решение задачи (14.5)-(14.7) ищем в виде ряда
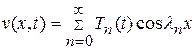 , (14.9)
, (14.9)
где
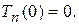 (14.10)
(14.10)
Подставив 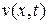 из (14.9) в (14.5) получим
из (14.9) в (14.5) получим
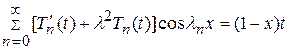 . (14.11)
. (14.11)
Для нахождения функции Tn(t) разложим функцию (1- х) в ряд Фурье по системе функций (14.8) на интервале (0,1):
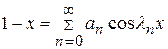 . (14.12)
. (14.12)
Так как
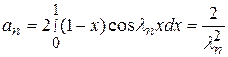 ,
,
и из (14.11) и (14.12) получаем уравнение
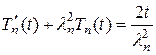 , (14.13)
, (14.13)
которое является обыкновенным неоднородным линейным дифференциальным уравнением первого порядка. Его общее решение найдем по формуле Эйлера
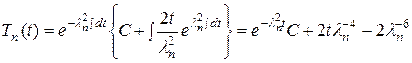
а с учетом условия (14.10), найдем решение задачи Коши
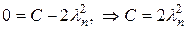
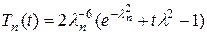 . (14.14)
. (14.14)
Из (14.4), (14.9) и (14.14) находим решение исходной задачи (14.1)- (14.3)
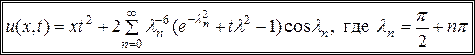 .▲
.▲
 2015-01-30
2015-01-30 1841
1841








