Меры информации

Понимая информацию как один из стратегических ресурсов общества, необходимо уметь его оценивать как с качественной, так и с количественной стороны. Здесь возникают проблемы из-за нематериальной природы этого ресурса и субъективного восприятия конкретной информации каждым конкретным человеком.

Для измерения информации вводятся два параметра: количество информации I и объем данных V _д. Эти параметры имеют разные выражения и интерпретацию в зависимости от рассматриваемой меры количества информации и объема данных.

Синтаксическая мера информации. Эта мера оперирует с обезличенной информацией, не выражающей смыслового отношения к объекту.

Объем данных V _д в сообщении измеряется количеством символов (разрядов) в этом сообщении. В различных системах счисления один разряд имеет различный вес и соответственно меняется единица измерения данных:

- в двоичной системе счисления единица измерения – бит (bit – binary digit) или более укрупненная единица байт, равная 8 бит. Сообщение, записанное двоичным кодом 10111011, имеет объем данных 8 бит или 1 байт.

- в десятичной системе счисления единица измерения – дит (десятичный разряд). Сообщение, записанное числом 275903 имеет объем данных 6 дит.

Количество информации I на синтаксическом уровне определяется с помощью понятия неопределенности состояния (энтропии) системы.

Пусть до получения информации потребитель имеет некоторые предварительные (априорные) сведения о системе α. Мерой его неосведомленности о системе является функция H (α), которая в то же время служит и мерой неопределенности состояния системы. После получения некоторого сообщения β получатель приобрел некоторую дополнительную информацию I β(α), уменьшившую его априорную неосведомленность так, что апостериорная (после получения сообщения β) неопределенность состояния системы стала H β(α). Тогда количество информации I β(α) о системе, полученной в сообщении β, определится как I β(α) = H (α) - H β(α), т.е. количество информации измеряется изменением (уменьшением) неопределенности состояния системы.

Если конечная неопределенность H β(α) обратится в нуль, то первоначальное неполное знание заменится полным знанием и количество информации I β(α) = H (α). Иными словами, энтропия системы H (α) может рассматриваться как мера недостающей информации.

Энтропия системы H(α), имеющая N возможных состояний, согласно формуле Шеннона, равна

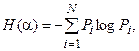
где P_i – вероятность того, что система находится в i -состоянии.

Для случая, когда все состояния системы равновероятны, т.е. их вероятности равны P_i =1/ N, ее энтропия определяется соотношением.

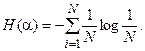
Часто информация кодируется числовыми кодами в той или иной системе счисления, особенно это актуально при представлении информации в компьютере. Естественно, что одно и то же количество разрядов в разных системах счисления может передать разное число состояний отображаемого объекта, что можно представить в виде соотношения

N = m ⁿ,

где N – число всевозможных отображаемых состояний;

m – основание системы счисления (разнообразие символов, применяемых в алфавите);

n – число разрядов (символов) в сообщении.

Пример. По каналу связи передается n-разрядное сообщение, использующее m различных символов. Так как количество всевозможных кодовых комбинаций будет N = mⁿ, то при равновероятности появления любой из них количество информации, приобретенной абонентом в результате получения сообщения, будет I = log N = n log m – формула Хартли.

Если в качестве основания логарифма принять m, то I = n. В данном случае количество информации (при условии полного априорного незнания абонентом содержания сообщения) будет равно объему данных I = V_д, полученных по каналу связи. Для неравновероятностных состояний системы всегда I < V_д = n.

Наиболее часто используются двоичные и десятичные логарифмы. Единицами измерения в этих случаях будут соответственно бит и дит.

Коэффициент (степень) информативности (лаконичность) сообщения определяется отношением количества информации к объему данных, т.е.

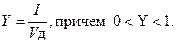
С увеличением Y уменьшаются объемы работы по преобразованию информации, для этого разрабатываются специальные методы оптимального кодирования информации.

Семантическая мера информации. Для измерения смыслового содержания информации, т.е. ее количества на семантическом уровне, наибольшее признание получила тезаурусная мера, которая связывает семантические свойства информации со способностью пользователя принимать поступившее сообщение. Для этого используют понятие тезаурус пользователя.

Тезаурус – это совокупность сведений, которыми располагает пользователь или система.

В зависимости от соотношений между смысловым содержанием информации S и тезаурусом пользователя S_p изменяется количество семантической информации I_c, воспринимаемой пользователем и включаемой им в дальнейшем в свой тезаурус.

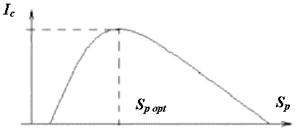
График зависимости количества семантической информации, воспринимаемой потребителем, от его тезауруса I_c = f (S_p)

Два предельных случая, когда количество семантической информации I_c равно 0:

- при S_p» 0 пользователь не воспринимает, не понимает поступающую информацию;

- при S_p ® ¥ пользователь все знает, и поступающая информация ему не нужна.

Максимальное количество I_c потребитель приобретает при согласовании ее смыслового содержания S со своим тезаурусом S_p (S_p = S_{p opt}), когда поступающая информация понятна пользователю и несет ему ранее неизвестные (отсутствующее в тезаурусе) сведения. Следовательно новых знаний, получаемых пользователем, является величиной относительной. Одно и то же сообщение может иметь смысловое содержание для компетентного пользователя и быть бессмысленным для пользователя некомпетентного. При оценке содержательного аспекта информации необходимо стремиться к согласованию величин S и S_p.

Относительной мерой количества семантической информации может служить коэффициент содержательности C, который определяется как отношение количества семантической информации к ее объему: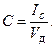

Прагматическая мера информации. Эта мера определяет полезность информации (ценность) для достижения пользователем поставленной цели, Эта мера также величина относительная, обусловленная особенностями использования этой информации в той или иной системе.

Пример. В экономической системе ценность информации можно определить приростом экономического эффекта ее функционирования, достигнутым благодаря использованию этой информации для управления системой.

Мера информации	Единицы измерения	Примеры (для компьютерной области)
Синтаксическая: шенноновский подход компьютерный подход	Степень уменьшения неопределенности Единицы представления информации	Вероятность события Бит, байт, Кбайт и т.д.
Семантическая	Тезаурус Экономические показатели	ППП, ПК, компьютерные сети и т.д. Рентабельность, производительность, коэффициент амортизации и т.д.
Прагматическая	Ценность использования	Емкость памяти, производительность компьютера, скорость передачи данных и т.д. Денежное выражение Время обработки информации и принятия решений