Метод потенциалов. Рассмотренный выше распределительный метод получения оптимального решения достаточно трудоемок

Рассмотренный выше распределительный метод получения оптимального решения достаточно трудоемок. В каждом допустимом решении для каждой свободной переменной необходимо строить циклы и определять изменение целевой функции. Ниже рассмотрена модификация распределительного метода, получившая название метода потенциалов. Этот метод рассмотрим как дальнейшее продолжение примера 4.

В соответствии с методом потенциалов каждой строке и каждому столбцу транспортной матрицы присваивается свой потенциал: строкам - потенциалы V_i, (i =1, 2,... п), столбцам - потенциалы U_j (j=1, 2,... т), как показано в табл. 3.5 для рассматриваемого примера.

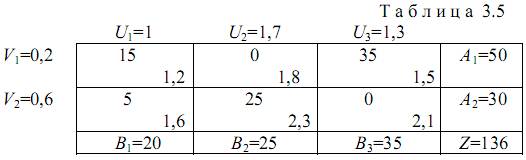
Эти потенциалы таковы, что для каждой базисной переменной сумма потенциалов равна удельной стоимости

Вернемся к соотношению (3.4), по которому вычислено изменение целевой функции при увеличении на единицу свободной переменной x₂₁, и заменим в этом соотношении потенциалами удельные стоимости базисных переменных

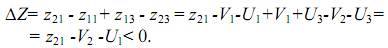
Из последнего соотношения видно, что при условии

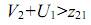
перевод свободной переменной х₂₁ в базис уменьшит целевую функцию Z.

Аналогично в соотношении (3.5), по которому вычислено изменение целевой функции при увеличении на единицу свободной переменной х₁₂, заменим потенциалами удельные стоимости базисных переменных

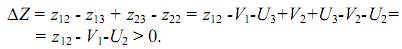
Из последнего соотношения видно, что при условии

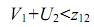
перевод свободной переменной x₁₂ в базис увеличивает целевую функцию Z.

В общем случае, при условии

перевод свободной переменной х_ij в базис уменьшает целевую функцию Z, а при условии

перевод свободной переменной х_ij в базис увеличивает целевую функцию Z.

Количество неизвестных потенциалов составляет (n+m), a количество базисных переменных (п+т-1). В системе уравнений (3.6) число неизвестных потенциалов на единицу больше числа уравнений. Следовательно, система (3.6) является неопределенной и имеет бесконечное количество решений.

Для получения одного из решений системы (3.6) произвольно зададимся величиной одного из потенциалов, например U₁=1. После этого все остальные потенциалы однозначно определятся по уравнениям (3.6).

В рассматриваемом случае имеем (табл. 3.5)

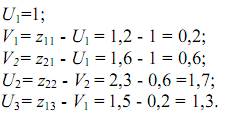
роверим условия (3.7) и (3.8) для свободных переменных в транспортной матрице табл. 3.5. Для свободной переменной х_23. Проверим условия (3.7) и (3.8) для свободных переменных в транспортной матрице табл. 3.5. Для свободной переменной х₂₃

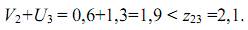
Следовательно, свободную переменную х₂₃ переводить в базис не следует, поскольку этот перевод приведет к увеличению целевой функции Z.

Для свободной переменной х₁₂

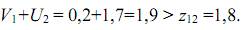
Следовательно, свободную переменную х₁₂ следует перевести в базис, поскольку этот перевод приведет к уменьшению целевой функции Z.

Для свободной переменной x₁₂ строим цикл пересчета (табл. 3.6) и из отрицательных вершин цикла выбираем меньшую базисную переменную х₁₁=15. Эта переменная перейдет в разряд свободных х₁₁=0, а переменная х₁₂ станет базисной х₁₂ =15. В соответствии со знаками в вершинах цикла базисная переменная х ₂₁ увеличится на 15 единиц и станет равной x₂₁=5+15=20, а базисная переменная х₂₂ уменьшится на 15 единиц и станет равной х₂₂=25-15=10.

Новому допустимому значению соответствует транспортная матрица табл. 3.7.

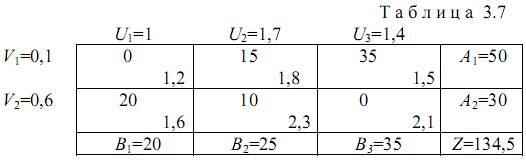
В этом решении свободные переменные х₁₁=0, х₁₃=0; базисные переменные х₁₂=15, х₁₃=35, х₂₁=20, x₂₂=10 е.м. Значение целевой функции

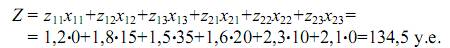
Проверим это решение на оптимальность. Произвольно зададимся значением одного из потенциалов U₁=1. В соответствии с уравнениями (3.6) остальные потенциалы будут равны

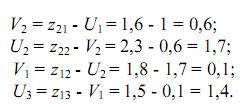
Для свободных переменных х₁₁ и х ₂₃ сумму потенциалов сопоставим с удельной стоимостью

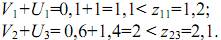
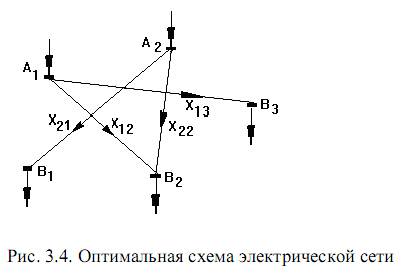
В соответствии с условием (3.8) перевод любой из этих переменных в базис приведет к увеличению целевой функции Z. Следовательно, полученное решение является оптимальным. Схема электрической сети, отвечающая оптимальному решению, показана на рис. 3.4.

Алгоритм решения транспортной задачи.

1. В соответствии с исходными данными составляется транспортная матрица размерностью пт, где п - количество источников питания, т - количество потребителей.

2. Находится допустимое решение, например методом наименьшей удельной стоимости.

3. Для допустимого решения каждой i -й строке и каждому j -му столбцу транспортной матрицы присваивается значение потенциала V_i и U_j (i =1,2,...n; j=1,2,.. .т). Для каждой базисной переменной сумма потенциалов равна удельной стоимости V_i+U_j=z_ij.

4. Произвольно задавшись значением одного из потенциалов, по уравнениям V_i+U_j=z_ij, справедливым для базисных переменных, вычисляются значения остальных потенциалов.

5. Для всех свободных переменных проверяется соотношение суммы потенциалов с удельной стоимостью. Если для всех свободных переменных V_i+U_j < z_ij, то полученное решение является оптимальным.

6. Если имеются свободные переменные, для которых V_i+U_j > z_ij, то выбирается любая из этих свободных переменных и переводится в базис. Для этого строится цикл пересчета (замкнутая ломаная линия), начальная вершина которого лежит в клетке выбранной свободной переменной. Остальные вершины цикла лежат в клетках, соответствующих базисным переменным. Начальной вершине цикла присваивается знак "+", соответствующий увеличению переменной. Далее знаки вершин цикла чередуются. Знаки "+" соответствуют увеличению базисных переменных, знаки "-" - их уменьшению.

7. Из отрицательных вершин цикла выбирается вершина с наименьшим значением базисной переменной и на эту величину изменяются все переменные, лежащие в вершинах цикла. В положительных вершинах переменные увеличиваются, в отрицательных - уменьшаются. При этом выбранная свободная переменная становится базисной, а наименьшая по величине базисная переменная в отрицательной вершине цикла становится свободной (равной нулю).

8. Для вновь полученного решения вычислительная процедура повторяется, начиная с пункта 3.