Кубическая интерполяция

Квадратичная интерполяция, которая рассматривалась в предыдущем разделе, называется методом Пауэлла и аппроксимирует функцию квадратным трехчленом. В этом разделе рассматривается метод Давидона, который гарантирует большую точность и аппроксимирует функцию кубическим полиномом.

Для кубической интерполяции в этом методе используются значения функции и ее производной, вычисленных в двух точках.

Рассмотрим задачу минимизации функции f(x) на прямой x₀ + hd, то есть минимизацию функции

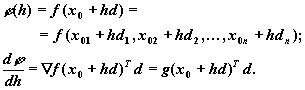
Предположим, что известные следующие значения:

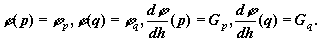
Эту информацию можно использовать для построения в кубического полинома

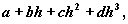
который будет аппроксимировать функцию (h) Если p=0, то уравнения, которые определяют a, b, c, d имеют вид:

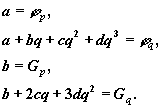
Точки перегиба кубического полинома являются решением уравнения

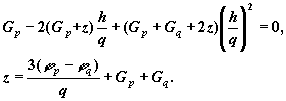
Следовательно, если r является точкой минимума кубического полинома,

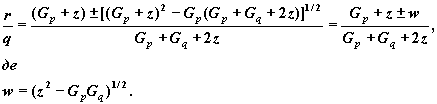
Одно из значений этого выражения является минимумом. Друга производная равна 2c +6dh

Если мы выберем положительный знак, то при

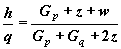
друга производная будет

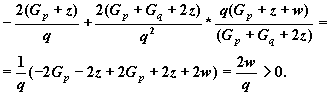
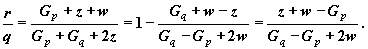(2.1)

Выбор точки q зависит от нас. Если G_p >0, то надо выбрать значение q положительным, то есть сделать шаг в направлении уменьшения функции (h), в другом случае значения q надо выбирать отрицательным. Значение должно быть таким, чтобы интервал (0,) включал в себя минимум. Это будет верным, если _q >  _p или G_p >0.

Если ни одно из этих условий не исполняется, то мы удваиваем значения q, повторяя это в случае необходимости, пока указанный интервал не будет содержать в себе минимум.

Давидон, Флетчер и Пауэлл предложили выбирать q следующим чином:

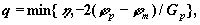
где  _m - оценка самого малого значения истинного минимумf (h), а  - константа, значение которой обычно берут 2 или 1.

итерационная процедура:
1. Найт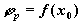и и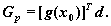
2. Проверить, если не выполняется условие G_p < 0, то выполнять поиск в направлении -d. Выбрать q из выражения. При этом надо "угадать" _m.
3. Вычислить 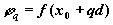и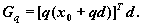
4. Если G_q < 0 или _q > _p, то интервал, который содержит минимум, найден. В другом случае изменить q на 2q и возвратиться к шагу 3.
5. Использовать уравнение (2.1) для апроксимации точки минимума на интервале (0, q) значением r.
6. Если 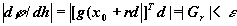, где  - заданная точность, то остановиться.
7. Возвратиться на шаг 5, используя интервал (0,r), если G_r > 0, или используется интервал (r,q), если G_r 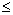0.

Квадратичные функции

Квадратичная функция

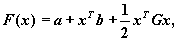(1)

где a - стала; b - постоянный вектор и G - положительно определенная симметричная матрица - имеет минимум в точке x ^*, где x ^* определяется следующим путем:

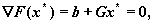(2)

оттуда x*= -G^-1 b. Любую функцию можно аппроксимировать в окресности точки x₀ функцией

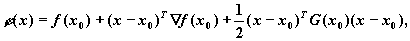(3)

где G(x₀) - матрица Гессе, вычисленная в точке x₀.

Аппроксимацией минимума функции f(x) может быть минимум функции  (x). Если последний находится в точке x_m, то

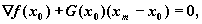
оттуда

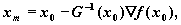
или

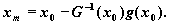(4)

Таким образом точкой x_и следующей аппроксимации минимума будет:

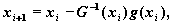(5)

или,

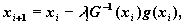(6)

где длина шага  _и определяется одномерным поиском в направлении G^-1(x_и) g(x_и).

Метод Ньютона-Рафсона основан на последнем уравнении.

Уравнения (5) и (6) в том виде, как они записаны, требуют вычисления и транспонирования матрицы Гессе на каждом шаге, который чаще является главной частью вычислений. Если точка x_и близко расположенная к точке x ^*, то сходимость будет быстрой, потому, что в общем случае функция  (x) будет хорошо аппроксимировать функцию f(x) в этой ячейке. Как норму градиента  g(x_и+1) , так и расстояние между точками  x_и+1 - x_и  надо проверить на выполнение критерий завершения. Интересно отметить, что сравнивая с простым методом самого быстрого спуска направлением спуска в данном случаю будет не -g(x_и), а - G^-1(x_и) g(x_и), где учитываются и вторые сменные. Методом Давидона - Флетчера - Пауэлла можно получить самый лучший результат, делая поиск на и -му этапе в направлении - H_и g(x_и), где H_и - положительно определенная симметричная матрица, которая в конечном счете будет приравнивать - G^-1(x*). Таким образом, этот метод обходит как вычисления, так и транспонирование матрицы G(x_и) при каждой итерации.

Следовательно, направление поиска при каждой итерации является решающим фактором, если говорить об эффективности итерационных методов поиска. При каждой итерации желательно провести одномерный поиск в самом лучшем направлении. Для квадратичной функции переменных вида (1) самым лучшим направлением является направление, сопряженное с предыдущим направлением поиска.

Говорят, что два направления p и q сопряженные относительно симметричной положительно определенной матрицы G, если

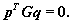(7)

Можно показать, что если p₀, p₁,:,p_n-1 это n взаимно сопряженных направлений в n -мерном пространстве, то они ленейно независимые.

Перепишем функцию (1) в виде

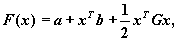
причем ее минимум находится в точке

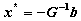
и

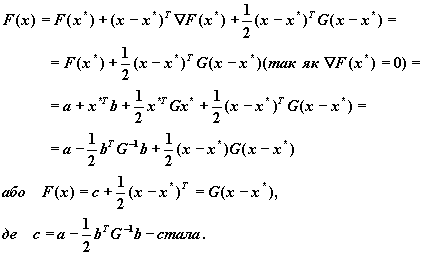(8)

Допустим, что для поиска минимума функции (8) используется итерационная процедура.

Начнем из точки x₀ и проведем поиск в направлении p₀ с целью нахождения минимума в точке

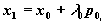(9)

где  ₀ - некоторая скалярная величина.

Отметим, что в точке x₁ направление 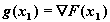ортогональный направлению p₀ и

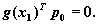(10)

В общему случаю на шаге и происходит поиск из точки x_и в направлении p_и с целью нахождения минимума в точке

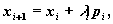(11)

где для F(x) справедливые соотношения

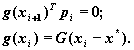(12) (13)

Повторным применением уравнения (11) после шагов получим

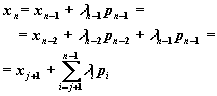(14)

для всех j на промежутке 0 j<n-1.

Таким образом, согласно уравнению (13)

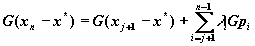(15)

Следовательно,

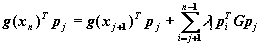(16)

и из уравнения (16) получим:

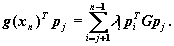
Сейчас, если все векторы p₀,p₁,:,p_n-1 взаимно сопряженные так, что 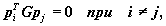то из соотношения (12) получим

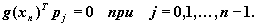
Но потому, что в этом случае векторы p₀,p₁,:,p_n-1 ленейно независимые и, таким образом, образовывают базис, то

g(x_n)=0

оттуда

G(x_n - x*)=0

и

x_n = x*.

Следовательно, если поиск проводится по взаимно сопряженным направлениям, то минимум квадратичной функции n переменных будет найден не больше чем за n шагов.