Классический анализ СМО с потерями принадлежит А.К.Эрлангу. Он исследовал модель, представленную на рис. 7.2. Условия задачи:
 |
Имеется m обслуживающих приборов, каждый из которых доступен, когда он свободен, для любой заявки на обслуживание.
Заявки образуют простейший поток событий интенсивности l (7.3).
Длительность обслуживания одной заявки одним обслуживающим прибором подчиняется экспоненциальному распределению g(t)= m e-mt, t>0, (7.5)
Где 1/ m – средняя длительность обслуживания.
4. Если в момент поступления заявки все приборы заняты, то заявка теряется.
Требуется определить вероятности pk (t), k= 0,1,…, m, состояний системы, то есть вероятности того, что в любой момент времени t будет занято ровно k обслуживающих приборов.
Процесс функционирования данной СМО удобно представить марковской цепью. Она характеризуется вероятностями состояний и вероятностями переходов из одних состояний в другие.
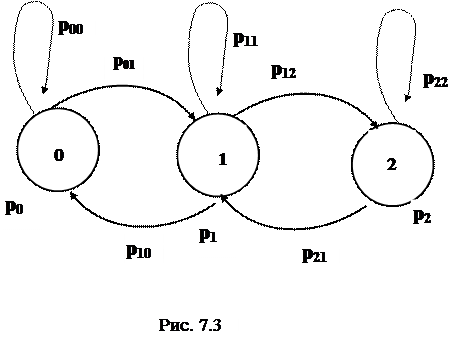 |
Рассмотрим случай для m=2. Тогда система будет иметь три состояния: k=0 –свободны все приборы, k=1 - занят один прибор, k=2 – заняты оба прибора. Диаграмма переходов из состояния в состояние показана на рис. 7.3.
|
|
|
Для исследования поведения системы в любой момент времени составляют систему дифференциальных уравнений по методу, хорошо изложенному в учебнике Е.С. Вентцель. Решения указанных уравнений полезны для анализа переходных процессов в системе. В установившемся режиме анализ существенно упрощается: достаточно воспользоваться уравнением равновесного состояния
lpk-1= k m pk (7.6)
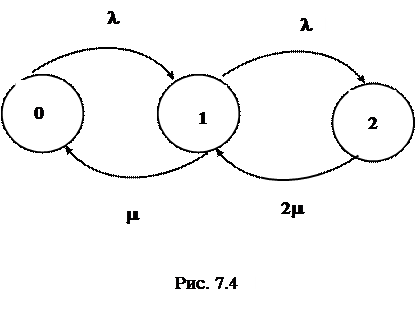 |
Оно сходно уравнению Кирхгофа в электротехнике и выражает тот факт, что интенсивность потока из любого состояния равна суммарной интенсивности потока в
это же состояние. Анализ удобно проводить по диаграмме переходов, представленной на рис.7.4.
Из (7.6) при k=1 имеем
lp0=mp1,
или p1=rp0, (7.7)
где r=l/m.
При к=2 из того же уравнения получаем:
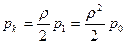 .
.
В общем случае имеем
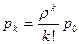 (7.8)
(7.8)
Следует также помнить, что
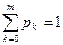 . (7.9)
. (7.9)
Тогда, с учетом (4.8), получаем, что
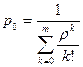 . (7.10)
. (7.10)
В итоге формула (4.8) принимает вид
 . (7.11)
. (7.11)

и называется формулой Эрланга.
Она дает предельный закон распределения числа занятых каналов в зависимости от характеристик потока заявок и производительности приборов обслуживания.
При k=m из (7.11) получаем вероятность того, что поступившая заявка найдет все приборы занятыми, то есть вероятность отказа pотк = pm.
Если в системе только один прибор, то вероятность свободного состояния:
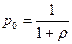 . (7.12)
. (7.12)
Вероятность отказа
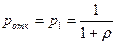 . (7.13)
. (7.13)
Среднее число попыток получить доступ к обслуживаемому прибору
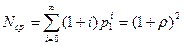 . (7.14)
. (7.14)
 2015-01-30
2015-01-30 1424
1424








