1. Математическое ожидание постоянной величины равно са мой постоянной: 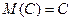 .
.
□ Постоянную величину С можно рассматривать как величину, принимающую значение С с вероятностью 1. Поэтому М(С) = С·1 = 1.■
2. Постоянный множитель можно выносить за знак математического ожидания, т.е. M(kX) = kM(X).
□ Так как случайная величина kX принимает значения kxi (i = 1,2,...,n), то 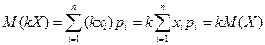 ■
■
3. Математическое ожидание алгебраической суммы конечного числа случайных величин равно такой же сумме их математических ожиданий, т.e. М (Х ± У) = М(Х) ± М(У).
□ В соответствии с определением суммы и разности случайных величин Х+У (Х-У) представляют случайную величину, которая принимает значения xi+yj (xi-yj) (i = 1,2,...,n) (j = 1,2,...,m) с вероятностями рij = Р[(Х = хi)(У = yj)].
Поэтому 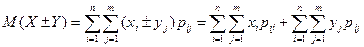 .
.
Так как в первой двойной сумме xi не зависит от индекса j, по которому ведется суммирование во второй сумме, и аналогично во второй двойной сумме yj не зависит от индекса i, то
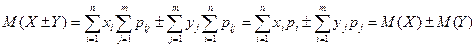 .■
.■
4. Математическое ожидание произведения конечного числа независимых случайных величин равно произведению их математических ожиданий: М(ХУ) = М(Х)М(У).
|
|
|
□ В соответствии с определением произведения случайных величин, ХУ представляет собой случайную величину, которая принимает значения xiyi (i = 1,2,...,n) (j = 1,2,...,m) с вероятностями Рij = P[(Х = хi)(У = yj)], причем в силу независимости Х и У pij = pipj. Поэтому 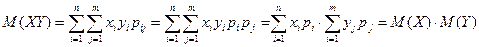 .■
.■
5. Если все значения случайной величины увеличить (уменьшить) на постоянную С, то на эту же постоянную С увеличится (уменьшится) математическое ожидание этой случайной величины: М(Х ± С) = М(Х) ± С.
□ Учитывая свойства 3 и 1 математического ожидания, получим М(Х ± С) = М(Х) ± М(С) = М(Х) ± С.■
6. Математическое ожидание отклонения случайной величины от ее математического ожидания равно нулю: М[Х-М(Х)] =0.
□ Пусть постоянная С есть математическое ожидание а = М(Х), т.е. С = а. Тогда, используя свойство 5, получим
М(Х - а) = М(Х) - а = а - а = о. ■
15. Дисперсия дискретной случайной величины и ее свойства (с выводом). Примеры.
Определение. Дисперсией D(Х) случайной величины Х называется математическое ожидание квадрата ее отклонения от математического ожидания:
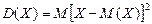 или или 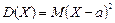 , где , где 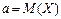
|
Доказательство. С учетом того, что мат ожид М(Х) и квадрат мат-го ожид М2(Х) – величины постоянные, можно записать:
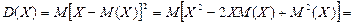
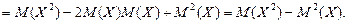
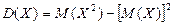
В качестве характеристики рассеяния нельзя брать математическое ожидание отклонения случайной величины от ее математического ожидания 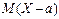 , ибо согласно свойству 6 математического ожидания эта величина равна нулю для любой случайной величины.
, ибо согласно свойству 6 математического ожидания эта величина равна нулю для любой случайной величины.
Выбор дисперсии, определяемой по формуле, в качестве характеристики рассеяния значений случайной величины Х оправдывается также тем, что, как можно показать, математическое ожидание квадрата отклонения случайной величины Х от постоянной величины С минимально именно тогда, когда эта постоянная С равна математическому ожиданию 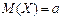 , т.е.
, т.е. 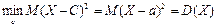 .
.
|
|
|
Если случайная величина Х - дискретная с конечным числом значений, то 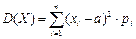 (3.11).
(3.11).
Если случайная величина Х - дискретная с бесконечным, но счетным множеством значений, то 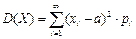 (если ряд в правой части равенства сходится).
(если ряд в правой части равенства сходится).
Дисперсия D(Х) имеет размерность квадрата случайной величины, что не всегда удобно. Поэтому в качестве показателя рассеяния используют также величину 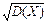 .
.
Определение. Средним квадратическим отклонением (стандартным отклонением или стандартом) 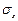 случайной величины Х называется арифметическое значение корня квадратного из ее дисперсии: случайной величины Х называется арифметическое значение корня квадратного из ее дисперсии:
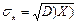
|
 2015-01-21
2015-01-21 673
673








