Свойства плотности вероятности непрерывной случайной величины

1. Плотность вероятности - неотрицательная функция, т.е. .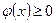

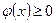☺ как производная монотонно неубывающей функции F(х). ☻

2. Вероятность попадания непрерывной случайной величины в интервал [а,b] равна определенному интегралу от ее плотности вероятности в пределах от а до b, т.е. .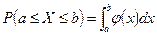

☺ Согласно свойству 4 функции распределения 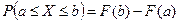. Так как F(x) - первообразная для плотности вероятности 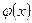(т.к. 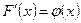, то по формуле Ньютона-Лейбница приращение первообразной на отрезке [а,b] – определенный интеграл . ☻

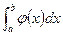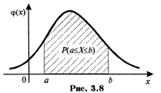
Геометрически полученная вероятность равна площади фигуры, ограниченной сверху кривой распределения и опирающейся на отрезок [а,b] (рис. 3.8).

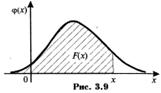
3. Функция распределения непрерывной случайной величины может быть выражена через плотность вероятности по формуле:

.

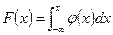Геометрически функция распределения равна площади фигуры, ограниченной сверху кривой распределения и лежащей левее точки х (рис. 3.9).

4. Несобственный интеграл в бесконечных пределах от плотности вероятности непрерывной случайной величины равен единице: .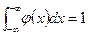

Геометрически свойства 1 и 4 плотности вероятности означают, что ее график - кривая распределения - лежит не ниже оси абсцисс, и полная площадь фигуры, ограниченной кривой распределения и осью абсцисс, равна единице.

19. Случайная величина, распределенная по биномиальному закону, ее математическое ожидание и дисперсия. Закон распреде­ления Пуассона.

Определение. Дискретная случайная величина Х имеет биномиальный закон распределения с параметрами npq, если она принимает значения 0, 1, 2,..., m,...,n с вероятностями

,

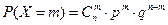где 0<р<l, q=1-p.

Как видим, вероятности Р(Х=m) находятся по формуле Бернулли, следовательно, биномиальный закон распределения представляет собой закон распределения числа Х=m наступлений события А в n независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью р.

Ряд распределения биномиального закона имеет вид:

Очевидно, что определение биномиального закона корректно, т.к. основное свойство ряда распределения 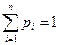выполнено, ибо 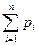есть не что иное, как сумма всех членов разложения бинома Ньютона:

Математическое ожидание случайной величины Х, распределенной по биноминальному закону,

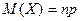а ее дисперсия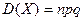

Определение. Дискретная случайная величина Х имеет закон распределения Пуассона с параметром λ > 0, если она принимает значения 0, 1, 2,..., m,... (бесконечное, но счетное множество значений) с вероятностями ,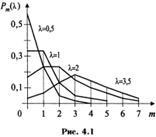

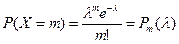Ряд распределения закона Пуассона имеет вид:

Очевидно, что определение закона Пуассона корректно, так как основное свойство ряда распределения 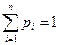выполнено, ибо сумма ряда .

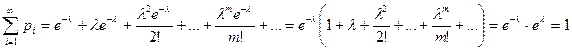На рис. 4.1 показан многоугольник (полигон) распределения случайной величины, распределенной по закону Пуассона Р(Х=m)=Р_m(λ) с параметрами λ = 0,5, λ = 1, λ = 2, λ = 3,5.

Теорема. Математическое oжидaниe и дисперсия случайной величины, распределенной по закону Пуассона, совпадают и равны параметру λ этого закона, т.е.

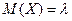и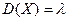

20. Математическое ожидание и дисперсия числа и частости на­ступлений события в п повторных независимых испытаниях (с выводом).

Математическое ожидание частости 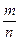события в n независимых испытаниях, в каждом из которых оно может наступить с одной и той же вероятностью р, равно р, т.е. 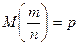а ее дисперсия .

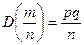□ Частость события 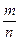есть 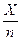, т.е. 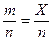, где Х - случайная величина, распределенная по биномиальному закону. Поэтому

. ■

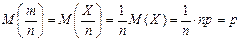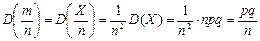21. Определение нормального закона распределения. Теоретико-вероятностный смысл его параметров. Нормальная кривая и зависимость ее положения и формы от параметров.

Определение. Непрерывная случайная величина Х имеет нормальный закон распределения (закон Гаусса) с параметрами а и 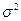, если ее плотность вероятности имеет вид:

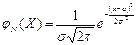
Термин «нормальный» не совсем удачный. Многие признаки подчиняются нормальному закону, например, рост человека, дальность полета снаряда и т.п. Но если какой-либо признак подчиняется другому, отличному от нормального, закону распределения, то это вовсе не говорит о «ненормальности» явления, связанного с этим признаком.

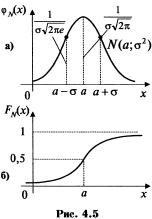
Кривую нормального закона распределения называют нормальной или гауссовой кривой. На рис. 4.5 а, б приведены нормальная кривая 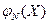с параметрами а и 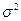, т.е. 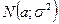, и график функции распределения случайной величины Х, имеющей нормальный закон.

Обратим внимание на то, что нормальная кривая симметрична относительно прямой х=а, имеет максимум в точке х=а, равный 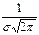, т.е. 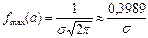, и две точки перегиба 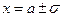с ординатой .

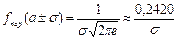Можно заметить, что в выражении плотности нормального закона параметры обозначены буквами а и 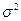, которыми мы обозначаем математическое ожидание М(Х) и дисперсию D(Х). Такое совпадение неслучайно. Рассмотрим теорему, устанавливающую теоретико-вероятностный смысл параметров нормального закона.

Теорема. Математическое ожидание случайной величины Х, распределенной по нормальному закону, равно параметру а этого закона, т.е. 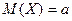, а ее дисперсия - параметру 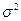, т.е. .

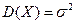□ Математическое ожидание случайной величины Х:

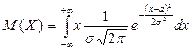. Произведем замену переменной, положив 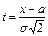. Тогда 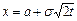и 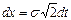, пределы интегрирования не меняются и, следовательно, .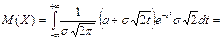

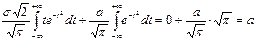(первый интеграл равен нулю как интеграл от нечетной функции по симметричному относительно начала координат промежутку, а второй интеграл 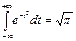- интеграл Эйлера­Пуассона).

Дисперсия случайной величины Х:

.

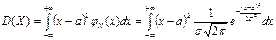Сделаем ту же замену переменной 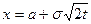, как и при вычислении предыдущего интеграла. Тогда

.

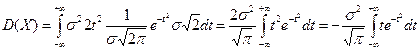Применяя метод интегрирования по частям, получим:

.■

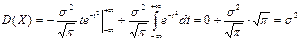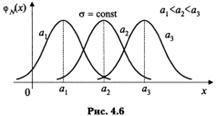
Выясним, как будет меняться нормальная кривая при изменении параметров а 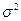и (или 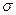). Если 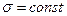, и меняется параметр а (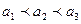), т.е. центр симметрии распределения, то нормальная кривая будет смещаться вдоль оси абсцисс, не меняя формы (рис. 4.6).

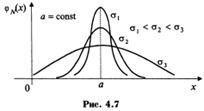Если a=const и меняется параметр 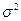(или 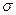), то меняется ордината максимума кривой 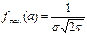. При увеличении 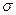ордината максимума кривой уменьшается, но так как площадь под любой кривой распределения должна оставаться равной единице, то кривая становится более плоской, растягиваясь вдоль оси абсцисс; при уменьшении а, напротив, нормальная кривая вытягивается вверх, одновременно сжимаясь с боков. На рис. 4.7 показаны нормальные кривые с параметрами 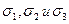, где 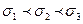. Т.о., параметр а (он же математическое ожидание) характеризует положение Центра, а параметр 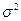(он же дисперсия) - форму нормальной кривой.

Нормальный закон распределения случайной величины с параметрами а=0, 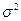=1, т.е. N(0;l), называется стандартным или нормированным, а соответствующая нормальная кривая - стандартной или нормированной.

22. Функция распределения нормально распределенной случай­ной величины и ее выражение через функцию Лапласа.

Сложность непосредственного нахождения функции распределения случайной величины, распределенной по нормальному закону, и вероятности ее попадания на некоторый промежуток связана с тем, что интеграл является «неберущимся». В элементарных функциях. Поэтому их выражают через функцию:

.

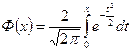- функцию (интеграл вероятностей) Лапласа, для которой составлены таблицы. Геометрически функция Лапласа представляет собой площадь под стандартной нормальной кривой на отрезке [-х; х] (рис. 4.8).

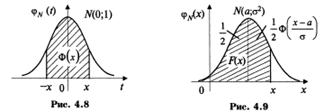
Теорема. Функция распределения случайной величины Х, распределенной по нормальному закону, выражается через функцию Лапласа Ф(х) по формуле:

.

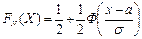□ По формуле 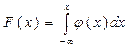функция распределения: .

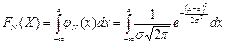Сделаем замену переменной, полагая 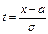, , 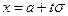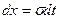при 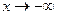, , 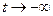поэтому

.

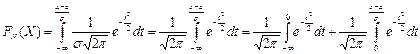Первый интеграл

.

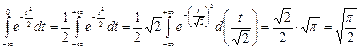(В силу четности подынтегральной функции и того, что интеграл Эйлера-Пуассона равен ).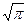

Второй интеграл с учетом 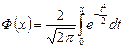составляет .

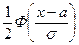Итак, . ■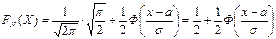

23. Формулы для определения вероятности: а) попадания нормально распределенной случайной величины в заданный интер­вал; б) ее отклонения от математического ожидания. Правило «трехсигм».

Свойства случайной величины, распределенной по нормальному закону:

1. Вероятность попадания случайной величины Х, распределенной по нормальному закону, в интервал 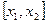, равна ,

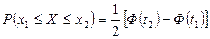Где , .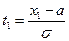

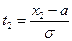□ Учитывая, что вероятность 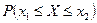есть приращение функции распределения на отрезке 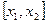и учитывая формулу 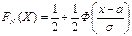получим:

. ■

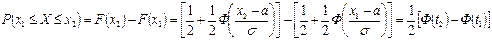2. Вероятность того, что отклонение случайной величины Х, распределенной по нормальному закону, от математического ожидания а не превысит величину 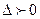(по абсолютной величине), равна 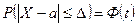, где .

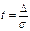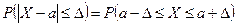□ . Учитывая свойство 1, а также свойство нечетности функции Лапласа, получим

. ■

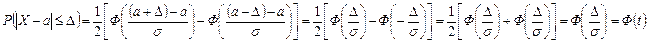«правило трех сигм»:

Если случайная величина Х имеет нормальный закон распределения с параметрами а и 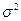, т.е. N(a; 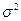), то практически достоверно, что ее значения заключены в интервале ().

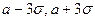Нарушение «правила трех сигм», т.е. отклонение нормально распределенной случайной величины Х больше, чем на 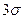(по абсолютной величине), является событием практически невозможным, так как его вероятность весьма мала:

.

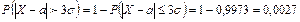24. Понятие двумерной (/7-мерной) случайной величины. При­меры. Таблица ее распределения. Одномерные распределения ее составляющих. Условные распределения и их нахождение по таб­лице распределения.

Очень часто результат испытания характеризуется не одной СВ, а некоторой системой случайных величин 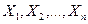, которую называют также многомерной (n-мерной) случайной величиной или случайным вектором Х = (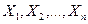). Приведем примеры многомерных случайных величин.

1. Успеваемость выпускника вуза характеризуется системой n случайных величин 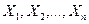- оценками по различным дисциплинам, проставленными в приложении к диплому.

2. Погода в данном месте в определенное время суток может быть охарактеризована системой случайных величин: 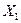- температура; 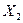- влажность; 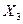- давление; 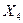- скорость ветра и т.п.

Любая СВ 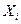(i = 1,2,...,n) есть функция элементарных событий ω, входящих в пространство элементарных событий Ω (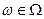). Поэтому и многомерная случайная величина есть функция элементарных событий ω: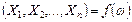

т.е. каждому элементарному событию ω ставится в соответствие несколько действительных чисел 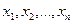, которые приняли случайные величины 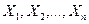в результате испытания. В этом случае вектор х = (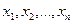) называется реализацией случайного вектора Х = ().

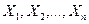Случайные величины 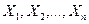, входящие в систему, могут быть как дискретными (см. выше пример 1), так и непрерывными (пример 2).

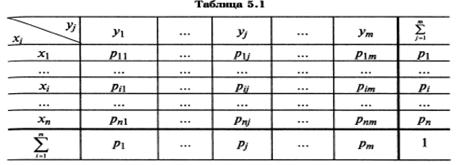Наиболее полным описанием многомерной СВ является закон ее распределения. При конечном множестве возможных значений многомерной СВ такой закон может быть задан в форме таблицы (матрицы), содержащей всевозможные сочетания значений каждой из одномерных случайных величин, входящих в систему, и соответствующие им вероятности. Так, если рассматривается двумерная дискретная случайная величина (X,Y), то ее двумерное распределение можно представить в виде таблицы (матрицы) распределения (табл. 5.1), в каждой клетке (i,j) которой располагаются вероятности произведения событий .

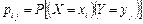Так как события 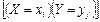(i = 1,2,...,n; j = 1,2,...,m), состоящие в том, что СВ Х примет значение 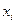, а СВ Y - значение 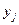, несовместны и единственно возможны, т.е. образуют полную группу, то сумма их вероятностей равна единице, т.е.: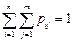

Распределение одномерной случайной величины Х можно получить, вычислив вероятность события 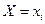(i = 1,2,...,n) как сумму вероятностей несовместных событий:

.

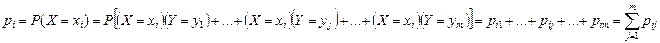Аналогично .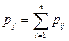

Т.о., чтобы по таблице распределения (табл. 5.1) найти вероятность того, что одномерная случайная величина примет определенное значение, надо просуммировать вероятности 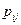из соответствующей этому значению строки (столбца) данной таблицы.

Если зафиксировать значение одного из аргументов, например, положить 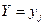, то полученное распределение случайной СВ Х называется условным распределением Х при условии 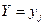. Вероятности 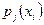этого распределения будут условными вероятностями события 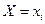, найденными в предположении, что событие 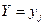произошло. Из определения условной вероятности:

.

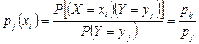Аналогично условное распределение СВ У при условии 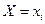задается с помощью условных вероятностей: .

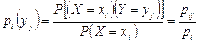25. Ковариация и коэффициент корреляции случайных величин. Связь между екоррелированностью и независимостью случай­ных величин.

Пусть имеется двумерная СВ (Х,Y), распределение которой известно, т.е. известна табл. 5.1 или совместная плотность вероятности 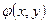. Тогда можно найти математические ожидания М(Х) = а_х, М(Y) = а_у и дисперси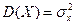и и 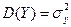одномерных составляющих Х и Y. Однако математические ожидания и дисперсии случайных величин Х и Y недостаточно полно характеризуют двумерную случайную величину (Х,Y), т.к. не выражают степени зависимости ее составляющих Х и Y эту роль выполняют ковариация и коэффициент корреляции.

Определение. Ковариацией (или корреляционным моментом) К_ху случайных величин Х и Y называется математическое ожидание произведения отклонений этих величин от своих математических ожиданий, т.е.

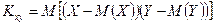, Или ,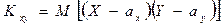

Где , .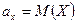

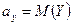Из определения следует, что 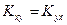. Кроме того, .

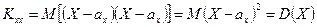т.е. ковариация СВ с самой собой есть ее дисперсия.

Для дискретных случайных величин: .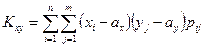

Для непрерывных случайных величин: .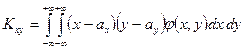

Ковариация двух случайных величин характеризует как степень зависимости случайных величин, так и их рассеяни е вокруг точки 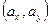. Об этом, в частности, свидетельствуют свойства ковариации случайных величин.

1. Ковариация двух независимых случайных величин равна нулю.

2. Ковариация двух случайных величин равна математическому ожиданию их произведения минус произведение математических ожиданий, т.е. 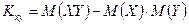, или .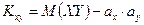

3. Ковариация двух случайных величин по абсолютной величине не превосходит произведения их средних квадратических отклонений, т.е. .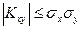

Ковариация, как уже отмечено, характеризует не только степень зависимости двух случайных величин, но и их разброс, рассеяние. Кроме того, она - величина размерная, ее размерность определяется произведением размерностей случайных величин. Это затрудняет использование ковариации для оценки степени зависимости для различных случайных величин. Этих недостатков лишен коэффициент корреляции.

Определение. Коэффициентом корреляции двух случайных величин называется отношение их ковариации к произведению средних квадратических отклонений этих величин:

.

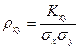Из определения следует, что 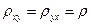. Очевидно также, что коэффициент корреляции есть безразмерная величина.

Свойства коэффициента корреляции:

1. Коэффициент корреляции принимает значения на отрезке [-1;1], т.е. .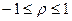

2. Если случайные величины независимы, то их коэффициент корреляции равен нулю, т.е. .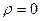

Случайные величины называются некоррелированными, если их коэффициент корреляции равен нулю. Т.о., из независимости случайных величин следует их некоррелированность. Обратное утверждение, вообще говоря, неверно: из некоррелированности двух случайных величин еще не следует их независимость.

3. Если коэффициент корреляции двух случайных величин равен (по абсолютной величине) единице, то между этими случайными величинами существует линейная функциональная зависимость.

26. Понятие о двумерном нормальном законе распределения. Условные математические ожидания и дисперсии.

Определение. Случайная величина (Х,Y) называется распределенной по двумерному нормальному закону, если ее совместная плотность имеет вид:

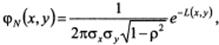
Где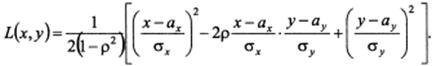

Из определения следует, что двумерный нормальный закон распределения определяется пятью параметрами: .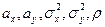

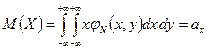и аналогично .;

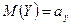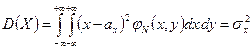и аналогично .;

.

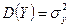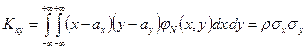Т.о., параметры 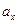и 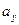выражают математические ожидания случайных величин Х и Y, параметры 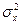и 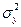- их дисперсии, а 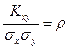- коэффициент корреляции между случайными величинами Х и Y.

Нетрудно убедиться в том, что каждый из условных законов распределения случайных величин Х и Y является нормальным с условным математическим ожиданием и условной дисперсией, определяемыми по формулам:

, ,

, .

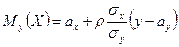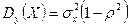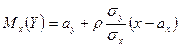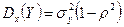Теорема. Если две нормально распределенные случайные величины Х и Y некоррелированы, то они независимы.

Т.о., для нормально распределенных случайных величин термины «некоррелированность» и «независимость» равносильны.

27. Неравенство Маркова (лемма Чебышева) (с выводом). При­мер.

Теорема. Если СВ Х принимает только неотрицательные значения и имеет математическое ожидание, то для любого положительного числа А верно неравенство:

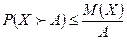
☺ Доказательство проведем для дискретной СВ Х. Расположим ее значения в порядке возрастания, из которых часть значений 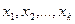будут не более числа А, а другая часть - 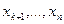будут больше А, т.е.

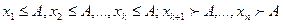(рис. 6.1).

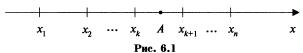
Запишем выражение для математического ожидания М(Х): ,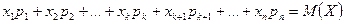

где 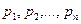- вероятности того, что СВ Х примет значения соответственно .

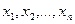Отбрасывая первые k неотрицательных слагаемых (напомним, что все 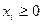), получим: .

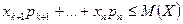Заменяя в неравенстве значения 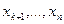меньшим числом А, получим более сильное неравенство: 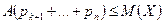или .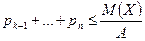

Cумма вероятностей в левой части полученного неравенства представляет собой сумму вероятностей событий 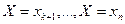, т.е. вероятность события Х>А. Поэтому .☻

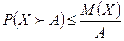Т.к. события Х > А и Х ≤ А противоположные, то заменяя Р(Х > А) выражением 1 - Р(Х ≤ А), придем к другой форме неравенства Маркова:

.

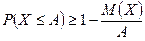Неравенство Маркова применимо к любым неотрицательным случайным величинам.

Пример. Среднее количество вызовов, поступающих на коммутатор завода в течение часа, равно 300. Оценить вероятность того, что в течение следующего часа число вызовов на коммутатор: а) превысит 400; б) будет не более 500.

Решение. а) По условию М(Х) = 300. По формуле 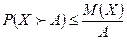: 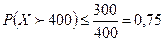т.е. вероятность того, что число вызовов превысит 400, будет не более 0,75.

б) По формуле 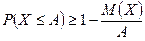: 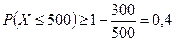т.е. вероятность того, что число вызовов не более 500, будет не менее 0,4.

28. Неравенство Чебышева (с выводом) и его частные случаидля случайной величины, распределенной по биномиальному за­кону, и для частости события.

Теорема. Для любой случайной величины, имеющей математическое ожидание и дисперсию, справедливо неравенство Чебышева: ,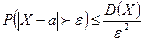

где а = М(Х), е > 0.

☺ Применим неравенство Маркова в форме 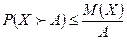к случайной величине 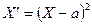, взяв в качестве положительного числа 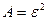. Получим: .

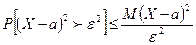Т.к. неравенство 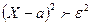равносильно неравенству 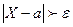, а 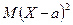есть дисперсия случайной величины Х, то из неравенства получаем доказываемое неравенство. ☻

Учитывая, что события 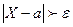и 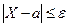противоположны, неравенство Чебышева можно записать и в другой форме: .

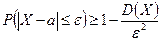Неравенство Чебышева применимо для любых случайных величин. В форме 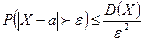оно устанавливает верхнюю границу, а в форме 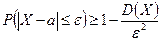- нижнюю границу вероятности рассматриваемого события.

Запишем неравенство Чебышева в форме 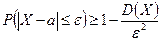для некоторых случайных величин:

а) для СВ Х = m, имеющей биноминальный закон распределения с математическим ожиданием а = М(Х) = nр и дисперсией D(X) = npq: .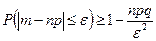

б) для частости 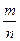события в n независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью 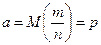и имеющей дисперсию : .

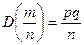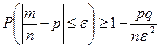3амечание. Если М(Х) > А или 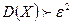, то правые части неравенств Маркова и Чебышева в форме соответственно 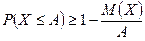и 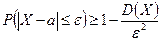будут отрицательными а в форме 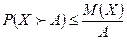и 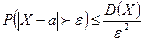будут больше 1.

Это означает, что применение указанных неравенств в этих случаях приведет к тривиальному результату: вероятность события больше отрицательного числа либо меньше числа, превосходящего 1.

30. Теорема Чебышева (с доказательством), ее значение и след­ствие. Пример.

Теорема. Если дисперсии n независимых случайных величин 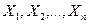ограничены одной и той же постоянной, то при неограниченном увеличении числа n средняя арифметическая случайных величин сходится по вероятности к средней арифметической их математических ожиданий 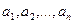, т.е.

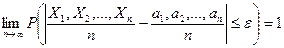
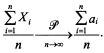
Или

☺ По условию 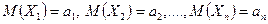, , 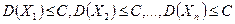где С - постоянное число.

Получим неравенство Чебышева в форме 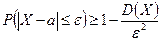для средней арифметической случайных величин, т.е. для .

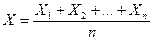Найдем математическое ожидание М(Х) и оценку дисперсии D(Х):

;

.

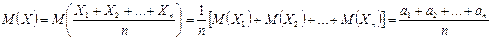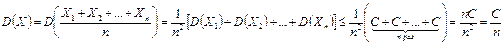(Здесь использованы свойства математического ожидания и дисперсии и, в частности, то, что случайные величины 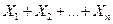независимы, а следовательно, дисперсия их суммы равна сумме дисперсий.)

Запишем неравенство 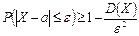для случайной величины :

.

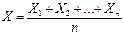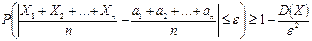Т.к. по доказанному 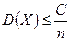, то ,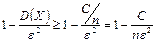

Следовательно .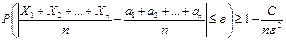

в пределе при n → ∞ величина 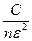стремится к нулю, и получим доказываемую формулу. ☻

Подчеркнем смысл теоремы Чебышева. При большом числе n случайных величин практически достоверно, что их средняя величина случайная, как угодно мало отличается от неслучайной величины, т.е. практически перестает быть случайной.

Следствие. Если независимые случайные величины 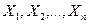имеют одинаковые математические ожидания, равные а, а их дисперсии ограничены одной и той же постоянной, то:

,

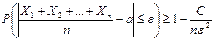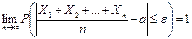
Или

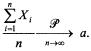
Теорема Чебышева и ее следствие имеют большое практическое значение. Например, страховой компании необходимо установить размер страхового взноса, который должен уплачивать страхователь; при этом страховая компания обязуется выплатить при наступлении страхового случая определенную страховую сумму. Рассматривая частоту/убытки страхователя при наступлении страхового случая как величину случайную и обладая известной статистикой таких случаев, можно определить среднее число/средние убытки при наступлении страховых случаев, которое на основании теоремы Чебышева с большой степенью уверенности можно считать величиной почти не случайной. Тогда на основании этих данных и предполагаемой страховой суммы определяется размер страхового взноса. Без учета действия закона больших чисел (теоремы Чебышева) возможны существенные убытки страховой компании (при занижении размера страхового взноса), либо потеря привлекательности страховых услуг (при завышении размера взноса).

31. Закон больших чисел. Теорема Бернулли (с доказательством) и ее значение. Пример.

Под законам больших чисел в широком смысле понимается общий принцип, согласно которому, по формулировке академика Колмогорова, совокупное действие большого числа случайных факторов приводит (при некоторых весьма общих условиях) к результату, почти не зависящему от случая. Другими словами, при большом числе случайных величин их средний результат перестает быть случайным и может быть предсказан с большой степенью определенности.

Теорема. Частость события в n повторных независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью p, при неограниченном увеличении числа n сходится по вероятности к вероятности р этого события в отдельном испытании:

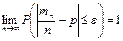
Или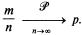

☺ Заключение теоремы непосредственно вытекает из неравенства Чебышева для частости события 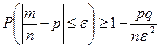при n → ∞. ☻

Смысл теоремы Бернулли состоит в том, что при большом числе n повторных независимых испытаний практически достоверно, что частость (или статистическая вероятность) события m/n - величина случайная, как угодно мало отличается от неслучайной величины р - вероятности события, т.е. практически перестает быть случайной.

Теорема Бернулли является следствием теоремы Чебышева.

32. Неравенство Чебышева для средней арифметической случай­ных величин (с выводом).

33. Центральная предельная теорема. Понятие о теореме Ляпу­нова и ее значение. Пример.

Центральная предельная теорема представляет собой группу теорем, посвященных установлению условий, при к-ых возникает нормальный закон распределения. Среди этих теорем важнейшее место принадлежит теореме Ляпунова.

Теорема Ляпунова. Если 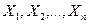независимые случайные величины, у каждой из которых существует матем-кое ожидание 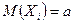, дисперсия 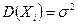, абсолютный центральный момент третьего порядка 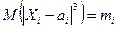и

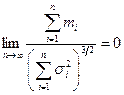(6.20)

то закон распределения суммы 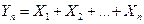при n → ∞ неограниченно приближается к нормальному с матем-ким ожиданием 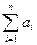и дисперсией .

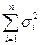Например, потребление электроэнергии для бытовых нужд за месяц в каждой квартире многоквартирного дома можно представить в виде n различных случайных величин. Если потребление электроэнергии в каждой квартире по своему значению резко не выделяется среди остальных, то на основании теоремы Ляпунова можно считать, что потребление электроэнергии всего дома, т.е. сумма n независимых случайных величин будет случайной величиной, имеющей приближенно нормальный закон распределения. Если, например, в одном из помещений дома разместится вычислительный центр, у которого уровень потребления электроэнергии несравнимо выше, чем в каждой квартире для бытовых нужд, то вывод о приближенно нормальном распределении потребления электроэнергии всего дома будет неправомерен, так как нарушено условие (6.20), ибо потребление электроэнергии вычислительного центра будет играть превалирующую роль в образовании всей суммы потребления.

Следствие. Если 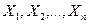- независимые случайные величины, у которых существуют равные математические ожидания 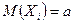, дисперсии 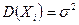и абсолютные центральные моменты третьего порядка 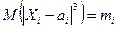(i = 1, 2,...n), то закон распределения суммы 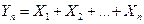при n → ∞ неограниченно приближается к нормальному закону.

В частности, если все случайные величины 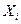одинаково распределены, то закон распределения их суммы неограниченно приближается к нормальному закону при n → ∞.

34. Вариационный ряд, его разновидности. Средняя арифмети­ческая и дисперсия ряда. Упрощенный способ их расчета.

Вариационным рядом называется ранжированный в порядке возрастания (или убывания) ряд вариантов с соответствующими им весами (частотами или частостями).

При изучении вариационных рядов наряду с понятием частоты используется понятие накопленной частоты (обозначаем 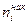). Накопленная частота показывает, ск-ко наблюдалось вариантов со значением признака, меньшим х. Отношение на копленной частоты к общему числу наблюдений n назовем накопленной частостью .

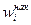Накопленные частоты (частости) для каждого интервала находятся последовательным суммированием частот (частостей) всех предшествующих интервалов, включая данный.

Для задания вариационного ряда достаточно указать варианты и соответствующие им частоты (частости) или накопленные частоты (частости).

Вариационный ряд называется дискретным, если любые его варианты отличаются на постоянную величину, и - непрерывным (интервальными), если варианты могут отличаться один от другого на сколь угодно малую величину.

Для графического изображения вариационных рядов наиболее часто используются полигон, гистограмма, кумулятивная кривая:

Полигон, как правило, служит для изображения дискретного вариационного ряда и представляет собой ломаную, в которой концы отрезков прямой имеют координаты (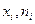), i = 1, 2,..., m.

Гистограмма служит только для изображения интервальных вариационных рядов и представляет собой ступенчатую фигуру из прямоугольников с основаниями, равными интервалам значений признака 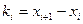, i = 1, 2,..., m, и высотами, равными частотам (частостям) 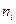(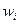) интервалов. Если соединить середины верхних оснований прямоугольников отрезками прямой, то можно получить полигон того же распределения.

Кумулятивная кривая (кумулята) - кривая накопленных частот (частостей). Для дискретного ряда кумулята представляет ломаную, соединяющую точки (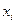, 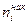) или (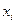, 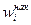), i = 1, 2,..., m. Для интервального вариационного ряда ломаная начинается с точки, абсцисса к-ой равна началу первого интервала, а ордината - накопленной частоте (частости), равной нулю. Другие точки этой ломаной соответствуют концам интервалов.

Эмпирической функцией pacпpeдeлeнuя 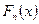называется относительная частота (частость) того, что признак (случайная величина х) примет значение, меньшее заданного х, т.е.

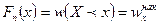
Другими словами, для данного х эмпирическая функция распределения представляет накопленную частость: .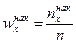

Вариационный ряд является статистическим аналогом (реализацией) распределения признака (случайной величины Х).

Вариационный ряд содержит достаточно полную информацию об изменчивости (вариации) признака. Однако обилие числовых данных, с помощью которых он задается, усложняет их использование. В то же время на практике часто оказывается достаточным знание лишь сводных характеристик вариационных рядов: средних или характеристик центральной тенденции; характеристик изменчивости (вариации) и др.

Средней арифметической вариационного ряда называется сумма произведений всех вариантов на соответствующие частоты, деленная на сумму частот:

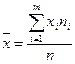
где 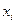- варианты дискретного ряда или середины интервалов интервального вариационного ряда; 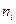- соответствующие им частоты; m - число неповторяющихся вариантов или число интервалов; .

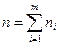Очевидно, что 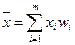, где 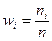- частости вариантов или интервалов.