1. Предположение о виде закона распределения м.б. выдвинуто исходя из теоретических предпосылок, опыта аналогичных предшествующих исследований и, наконец, на основании графического изображения эмпирического распределения.
2. Параметры распределения, как правило, неизвестны, поэтому их заменяют наилучшими оценками по выборке.
Критерии согласия отвечают на вопрос: объясняются ли расхождения между эмпирическим и теоретическим распределениями только случайными обстоятельствами, связанными с ограниченным числом наблюдений, или они являются существенными и связаны с тем, что теоретический закон распределения подобран неудачно.
Пусть необходимо проверить нулевую гипотезу Н0 о том, что исследуемая СВ Х подчиняется определенному закону распределения. Для проверки гипотезы Н0 выбирают некоторую СВ U, характеризующую степень расхождения теоретического и эмпирического распределений, закон распределения которой при достаточно больших n известен и практически не зависит от закона распределения СВ Х.
Зная закон распределения U, можно найти вероятность того, что U приняла значение не меньше, чем фактически наблюдаемое в опыте u, т.е. U ≥ u.
Если Р(U ≥ u) = α мала, то это означает в соответствии с принципом практической уверенности, что такие, как в опыте, и большие отклонения практически невозможны. В этом случае гипотезу Н0 отвергают.
Если же вероятность Р(U ≥ u) = α не мала, расхождение между эмпирическим и теоретическим распределениями несущественно и гипотезу Н0 можно считать правдоподобной или по крайней мере не противоречащей опытным данным.
46. Критерий согласия х2-Пирсона и схема его применения.
Критерии 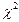 - Пирсона в качестве меры расхождения U берется величина
- Пирсона в качестве меры расхождения U берется величина 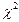 , равная сумме квадратов отклонений частостей (статистических вер-тей)
, равная сумме квадратов отклонений частостей (статистических вер-тей) 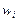 от гипотетических
от гипотетических 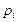 , рассчитанных по предполагаемому распределению, взятых с некоторыми весами
, рассчитанных по предполагаемому распределению, взятых с некоторыми весами 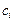 :
:
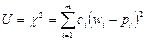 .
.
Веса 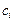 вводятся т.о., чтобы при одних и тех же отклонениях
вводятся т.о., чтобы при одних и тех же отклонениях 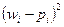 больший вес имели отклонения, при которых
больший вес имели отклонения, при которых 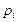 мала, и меньший вес - при которых
мала, и меньший вес - при которых 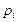 велика. Очевидно, этого удается достичь, если взять
велика. Очевидно, этого удается достичь, если взять 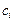 обратно пропорциональными вер-тям
обратно пропорциональными вер-тям 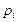 . Взяв в качестве весов
. Взяв в качестве весов 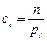 , можно доказать, что при n → ∞ статистика.
, можно доказать, что при n → ∞ статистика.
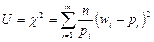 , или
, или 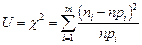 .
.
имеет 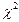 -распределение с k = m - r - 1 степенями свободы, где m - число интервалов эмпирического распределения (вариационного ряда); r - число параметров теоретического распределения, вычисленных по экспериментальным данным.
-распределение с k = m - r - 1 степенями свободы, где m - число интервалов эмпирического распределения (вариационного ряда); r - число параметров теоретического распределения, вычисленных по экспериментальным данным.
Числа 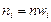 и
и 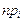 называются соответственно эмпирическими и теоретическими частотами.
называются соответственно эмпирическими и теоретическими частотами.
Схема применения критерия 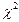 для проверки гипотезы Н0 сводится к следующему:
для проверки гипотезы Н0 сводится к следующему:
1. Определяется мера расхождения эмпирических и теоретических частот 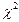 по
по 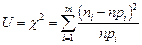
2. Для выбранного уровня значимости α по таблице 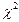 -распределения находят критическое значение
-распределения находят критическое значение 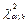 при числе степеней свободы k = m - r - 1.
при числе степеней свободы k = m - r - 1.
3. Если фактически наблюдаемое значение 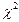 больше критического, т.е.
больше критического, т.е. 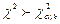 то гипотеза Н0 отвергается, если
то гипотеза Н0 отвергается, если 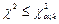 гипотеза Н0 не противоречит опытным данным.
гипотеза Н0 не противоречит опытным данным.
3амечание. Статистика 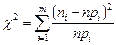 имеет
имеет 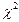 -распределение лишь при n → ∞, поэтому необходимо, чтобы в каждом интервале было достаточное количество наблюдений, по крайней мере 5 наблюдений. Если в каком-нибудь интервале число наблюдений ni< 5, имеет смысл объединить соседние интервалы, чтобы в объединенных интервалах
-распределение лишь при n → ∞, поэтому необходимо, чтобы в каждом интервале было достаточное количество наблюдений, по крайней мере 5 наблюдений. Если в каком-нибудь интервале число наблюдений ni< 5, имеет смысл объединить соседние интервалы, чтобы в объединенных интервалах 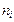 было не меньше 5.
было не меньше 5.
47. Функциональная, статистическая и корреляционная зависимости. Различия между ними. Основные задачи теории корреляции.
Функциональная зависимость (связь), когда каждому значению одной переменной соответствует вполне определенное значение другой.
Функциональная зависимость может иметь место как между детерминированными (неслучайными) переменными, так и между случайными величинами.
Статистическая (или стохастическая, вероятностная) зависимость - каждому значению одной переменной соответствует определенное (условное) распределение другой переменной.
Т.е. когда каждому значению одной переменной соответствует не какое-то определенное, а множество возможных значений другой переменной.
Возникновение понятия статистической связи обусловливается тем, что зависимая переменная подвержена влиянию ряда неконтролируемых или неучтенных факторов, а также тем, что измерение значений переменных неизбежно сопровождается некоторыми случайными ошибками.
В силу неоднозначности статистической зависимости между Y и Х для исследователя, в частности, представляет интерес усредненная по х схема зависимости, т.е. закономерность в изменении среднего значения - условного математического ожидания 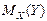 (математического ожидания случайной переменной Y, вычисленного в предположении, что переменная Х приняла значение х) в зависимости от х.
(математического ожидания случайной переменной Y, вычисленного в предположении, что переменная Х приняла значение х) в зависимости от х.
Определение. Статистическая зависимость между 2мя переменными, при которой каждому значению 1 переменной соответствует определенное условное математическое ожидание (среднее значение) другой, называется корреляционной.
Иначе, корреляционной зависимостью между двумя переменными величинами называется функциональная зависимость между значениями одной из них и условным математическим ожиданием другой.
Корреляционная зависимость м.б. представлена в виде:
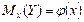 (1)
(1)
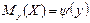 (2)
(2)
Предполагается, что 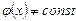 и
и 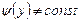 , т.е. если при изменении х или у условные математические ожидания
, т.е. если при изменении х или у условные математические ожидания 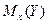 и
и 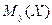 не изменяются, то говорят, что корреляционная зависимость между переменными Х и Y отсутствует.
не изменяются, то говорят, что корреляционная зависимость между переменными Х и Y отсутствует.
Сравнивая различные виды зависимости между Х и Y, можно сказать, что с изменением значений переменной Х при функциональной зависимости однозначно изменяется определенное значение переменной Y, при корреляционной - определенное среднее значение (условное математическое ожидание) Y, а при статистической - определенное (условное) распределение переменной Y. Т.о., из рассмотренных зависимостей наиболее общей выступает статистическая зависимость. Каждая корреляционная зависимость является статистической, но не каждая статистическая зависимость является корреляционной. Функциональная зависимость представляет частный случай корреляционной.
Уравнения (1) и (1) называются модельными уравнениями регрессии (или просто уравнениями регрессии) соответственно Y по Х и Х по Y, функции 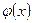 и
и 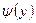 - модельными функциями регрессии (или функциями регрессии), а их графики - модельными линиями регрессии (или линиями регрессии).
- модельными функциями регрессии (или функциями регрессии), а их графики - модельными линиями регрессии (или линиями регрессии).
48. Линейная парная регрессия. Система нормальных уравнений для определения параметров прямых регрессии. Выборочная ковариация. Формулы для расчета коэффициентов регрессии.
Данные о статистической зав-ти удобно задавать в виде корреляционной таблицы.
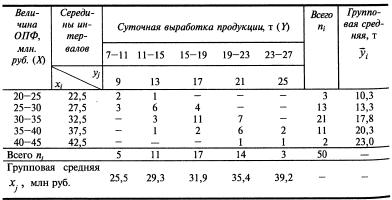
(В таблице через 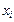 и
и 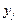 обозначены середины соответствующих интервалов, а
обозначены середины соответствующих интервалов, а 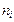 и
и 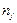 - соответственно их частоты).
- соответственно их частоты).
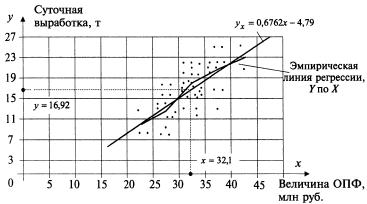
Изобразим полученную зав-ть графически точками координатной плоскости. Такое изображение статистической зав-ти наз-ся полем корреляции.
Для каждого значения 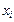 (i = 1,2,..., l), т.е. для каждой строки корреляционной таблицы вычислим групповые средние
(i = 1,2,..., l), т.е. для каждой строки корреляционной таблицы вычислим групповые средние
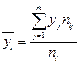
где 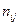 - частоты пар (
- частоты пар (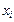 ,
, 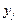 ) и
) и 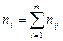 ; m - число интервалов по переменной Y.
; m - число интервалов по переменной Y.
Вычисленные групповые средние графически в виде ломаной, называемой эмпирической линией регрессии У по Х.
Аналогично для каждого значения 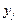 (j = 1,2,...,m):
(j = 1,2,...,m):
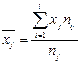 .
.
где 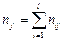 ; l - число интервалов по переменной Х.
; l - число интервалов по переменной Х.
По виду ломаной можно предположить наличие линейной корреляционной зав-ти У по Х между двумя рассматриваемыми переменными, которая графически выражается тем точнее, чем больше объем выборки n:
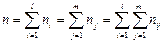
Поэтому уравнение регрессии будем искать в виде:
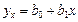 .
.
Применим метод наименьших квадратов, согласно которому неизвестные параметры 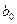 и
и 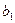 выбираются таким образом, чтобы сумма квадратов отклонений эмпирических групповых средних
выбираются таким образом, чтобы сумма квадратов отклонений эмпирических групповых средних 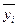 , от значений
, от значений 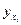 , найденных по уравнению регрессии, был минимальной:
, найденных по уравнению регрессии, был минимальной:
Система нормальных уравнений для определения параметров линейной регрессии:
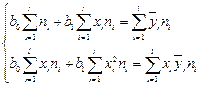
Или
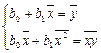 .
.
где соответствующие средние определяются по формулам:
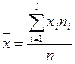 ,
, 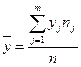 ,
, 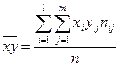 .
.
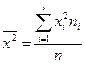 .
.
Подставляя значение 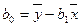 из первого уравнения системы в уравнение регрессии, получим:
из первого уравнения системы в уравнение регрессии, получим:
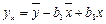 , или
, или 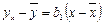 .
.
Коэффициент 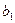 в уравнении регрессии, называемый выборочным коэффициентом регрессии (или просто коэффициентом регрессии) Y по Х, будем обозначать символом
в уравнении регрессии, называемый выборочным коэффициентом регрессии (или просто коэффициентом регрессии) Y по Х, будем обозначать символом 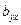 . Теперь уравнение регрессии У по Х запишется так:
. Теперь уравнение регрессии У по Х запишется так:
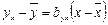 .
.
Коэффициент регрессии У по Х показывает, на сколько единиц в среднем изменяется переменная У при увеличении переменной Х на одну единицу.
Решая систему, найдем
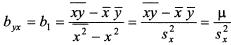
где 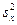 - выборочная дисперсия переменной Х:
- выборочная дисперсия переменной Х:
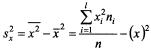
μ - выборочный корреляционный момент или выборочная ковариация:
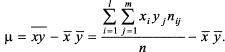
Рассуждая аналогично и полагая уравнение регрессии линейным, можно привести его к виду:
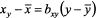 .
.
Где 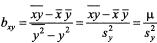 - выборочный коэффициент регрессии (или просто коэффициент регрессии) Х по Y, показывающий, на сколько единиц в среднем изменяется переменная Х при увеличении переменной У на одну единицу;
- выборочный коэффициент регрессии (или просто коэффициент регрессии) Х по Y, показывающий, на сколько единиц в среднем изменяется переменная Х при увеличении переменной У на одну единицу;
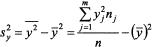 - выборочная дисперсия переменной У.
- выборочная дисперсия переменной У.
Упрощенный способ:
От значений переменных 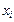 и
и 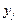 переходят к новым значениям
переходят к новым значениям
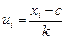 и
и 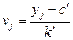
где k и k' - величины интервалов, а с и с' - середины серединных интервалов соответственно по переменной Х или У. Тогда:
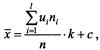
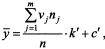
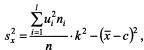
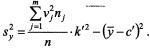
В этом случае формула для ковариации примет вид:
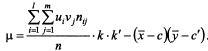
 2015-01-21
2015-01-21 1300
1300