В.Теорема 1. (Необходимое и достаточное условия возрастания функции)

1. Если дифференцируемая функция y=f(x) возрастает на [ a, b ], то ее производная неотрицательна на этом отрезке, f '(x) ≥ 0.

2. Обратно. Если функция y=f(x) непрерывна на [ a, b ], дифференцируема на (a, b) и ее производная положительна на этом отрезке, f ' (x) ≥ 0 для a<x<b, то f(x) возрастает на[ a, b ].

Доказательство.

1. Докажем первую часть теоремы. Итак, пусть функция y=f(x) возрастает на [ a, b ]. Зафиксируем на этом отрезке произвольную точку x, придадим ей приращение Δ x. Тогда если Δ x >0, то x<x+ Δ x. Поэтому по определению возрастающей функции f(x)<f(x+ Δ x), то есть f(x+ Δ x) - f(x)> 0. Но тогда и 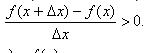Аналогично, если Δ x< 0, то x>x+ Δ x и значит f(x+ Δ x)-f(x)< 0, а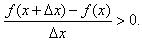

Переходя в этом равенстве к пределу при Δ x →0, получим 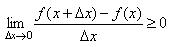, то есть f '(x) ≥0.

2. Докажем вторую часть теоремы. Пусть f '(x)> 0при всех x Î (a,b). Рассмотрим два любых значения x ₁ и x ₂ таких, что x ₁ < x ₂. Нужно доказать, что f(x ₁ )< f(x ₂ ). По теореме Лагранжа существует такое число c 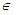(x ₁, x ₂ ), что 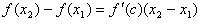. По условию f '(x)> 0, x ₁ – x ₂>0 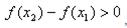, а это и значит, что f(x) – возрастающая функция.

3. Аналогичная теорема имеет место и для убывающих функций.

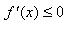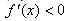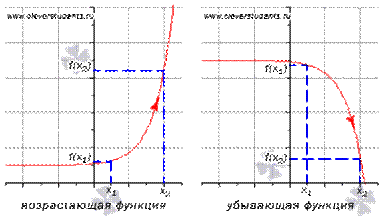
Теорема 2. Если f(x) убывает на[ a,b ], то на этом отрезке. Если на (a; b), то f(x) убывает на [ a, b ],в предположении, что f(x) непрерывна на [ a, b ]. Доказанная теорема выражает очевидный геометрический факт. Если на [ a, b ] функция возрастает, то касательная к кривой y=f(x) в каждой точке этого отрезке образует острый угол с осью Ox или горизонтальна, т.е. tg a≥0, а значит f '(x) ≥0. Аналогично иллюстрируется и вторая часть теоремы. Таким образом, возрастание и убывание функции характеризуется знаком ее производной. Чтобы найти на каком промежутке функция возрастает или убывает, нужно определить, где производная этой функции только положительна или только отрицательна, то есть решить неравенства f '(x) >0 – для возрастания или f '(x)< 0 – для убывания.