2015-01-21
607
Пусть функция f (x) дважды дифференцируема (имеет вторую производную) на интервале (a, b), тогда:
если f '' (x) > 0 для любого x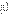 
(a, b), то функция f (x) является вогнутой на интервале (a, b);
если f '' (x) < 0 для любого x 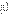(a, b), то функция f (x) является выпуклой на интервале (a, b).
Точка, при переходе через которую функция меняет выпуклость на вогнутость или наоборот, называется точкой перегиба. Отсюда следует, чтоесли в точке перегиба x 0 существует вторая производная f '' (x 0), то f '' (x 0) = 0.
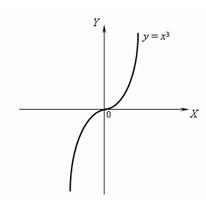
Пример:Рассмотрим график функции y = x 3 :
Эта функция является вогнутой при x > 0 и выпуклой при x < 0. В самом деле, y'' = 6 x, но 6 x > 0 при x > 0 и 6 x < 0при x < 0,следовательно, y'' > 0 при x > 0 и y'' < 0 при x < 0, откуда следует, что функция y = x 3 является вогнутой при x > 0 и выпуклой при x <0. Тогда x = 0 является точкой перегиба функции y = x 3.
35.Точка, отделяющая выпуклую часть кривой от вогнутой называется точкой перегиба. Достаточный признак сущ-я точки перегиба:Если для ф-и y=f(x) в т. Х0 вторая производная обращается в 0 при переходе через эту точку меняет знак, то точка с координатами х0, у0 будет т.перегиба ф-и
36. Наибольшее и наименьшее значение ф-и на отрезке. Дано: у=f(x) – ф-я непрерывная на отрезке [a;в] Найти, при каких х ф-я принимает наименьшее m и наибольшее М на отрезке. Решение: 1) найти крит-ю точку функции принадлежащие отрезку [а;в] 2) вычислить значение ф-и в этих точках и на концах отрезка 3) выбрать из полученных значений наименьшее и наибольшее
37. Асимптота: Прямая, называется асимптотой кривой заданной уравнением у=f(х), если при удалении точки М, лежащей на кривой от начала координат, расстояние от т. М до прямой стремится к 0. Вертикальные асимптоты.х=Q – называется вертикальной асимптотой графика у=f(х) если хотя бы один из односторонних пределов будет = бесконечности. Вертикальные асимптоты – это нули знаменателя ф-и или граничные точки области определения. Прямая у=в является горизонтальной асимптотой у= f(х) к графику ф-и у= f(х) если при стремлении lim f(x) = lim f(x) = в х-> -беск х->+беск Горизонтальные асимптоты есть отношение многочлена в 1-й степени. Накл асимпт. Прямая, y=kx+b будет наклонной асимптотой к гр-ку ф-и у= f(х) если сущ-т конечные пределы при lim f(x)/x=k х->к беск Lim(f(x) – kx)=в - формулы для определения параметров k и в x->к беск
38. схема полного исследования ф-и 1) Область определения 2) Точки разрыва(если имеются) 3) Точки пересечения с осями координат 4) Четность нечетность ф-и 5) Экстремум ф-и. Промежутки монотонности 6) Точки перегиба. Промежутки выпуклости, вогнутости 7) Асимптоты(если имеются) 8) Дополнительные точки(если требуются) 9) Построение графика.
