1. Показательное уравнение 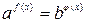 равносильно уравнению:
равносильно уравнению:
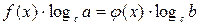 ,
,
которое получается логарифмированием исходного уравнения по какому-либо основанию 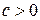 ,
, 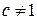 . В частности, уравнение
. В частности, уравнение 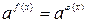 равносильно уравнению:
равносильно уравнению: 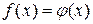 .
.
2. Корнями уравнения 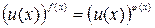 считаются только решения смешанной системы:
считаются только решения смешанной системы:
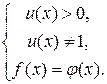
3. Логарифмическое уравнение: 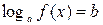 равносильно уравнению:
равносильно уравнению: 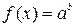 .
.
4. Логарифмическое уравнение: 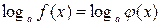 равносильно каждой из следующих систем:
равносильно каждой из следующих систем:
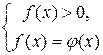 или
или 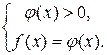
Для решения исходного уравнения переходят только к одной из этих систем (той, которая проще), либо решают уравнение 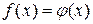 , которое может иметь корни, посторонние для исходного уравнения, и проверяют каждый из них подстановкой в исходное уравнение.
, которое может иметь корни, посторонние для исходного уравнения, и проверяют каждый из них подстановкой в исходное уравнение.
5. Показательное неравенство: 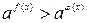 , равносильно неравенству:
, равносильно неравенству:
при 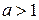
| при 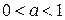
|
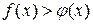
| 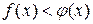
|
6. Логарифмическое неравенство:
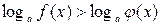
равносильно системе неравенств
при 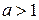
| при 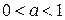
|
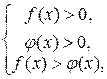
| 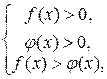
|
 Примеры решения задач
Примеры решения задач
1. Решить уравнение:
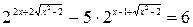 .
.
Решение. Сначала преобразуем исходное уравнение. Уравнение примет вид: 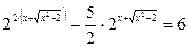 .
.
Это квадратное уравнение относительно величины: 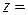
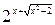 :
:
|
|
|
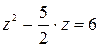 или
или 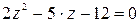 .
.
Находим его корни: 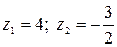 .
.
Поскольку величина 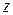 , как показательная функция, положительна при любом значении
, как показательная функция, положительна при любом значении 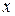 , то второй корень отбрасываем, как посторонний.
, то второй корень отбрасываем, как посторонний.
Итак, 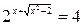 , откуда
, откуда 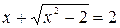 .
.
Уединяя радикал и возводя обе части уравнения в квадрат, получим:
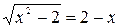 ,
,
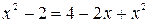 ,
,
откуда: 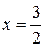 .
.

2. Решить неравенство:
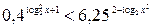 .
.
Решение. Заметив, что 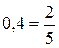 и
и 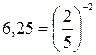 , приведем обе части неравенства к одному основанию:
, приведем обе части неравенства к одному основанию:
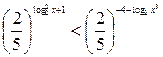 .
.
Так как основание степени 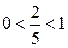 , то имеем:
, то имеем:
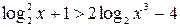 .
.
Функция 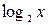 определена при
определена при 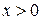 , поэтому:
, поэтому: 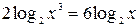 . Полагая,
. Полагая, 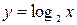 , приходим к неравенству:
, приходим к неравенству:
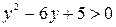 ,
,
откуда вытекает, что 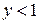 и
и 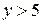 .
.
Таким образом, исходное неравенство равносильно совокупности неравенств:

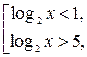 или поскольку основание логарифма >1, то
или поскольку основание логарифма >1, то 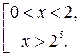
Итак, получаем ответ: 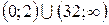 .
.

3. Решить неравенство:
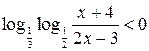 .
.
Решение. Согласно свойствам логарифмов, имеем 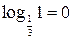 . Поскольку основание логарифма
. Поскольку основание логарифма 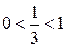 , получаем равносильное неравенство:
, получаем равносильное неравенство: 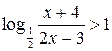 (при этом
(при этом 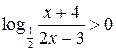 выполняется автоматически).
выполняется автоматически).
Далее, имеем 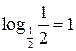 и так как
и так как 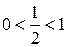 , то получаем равносильную данному неравенству систему:
, то получаем равносильную данному неравенству систему:
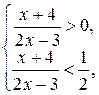 т.е.
т.е. 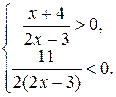
Из второго неравенства системы следует, что 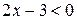 ; значит,
; значит, 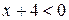 и задача сводится к решению равносильной системы:
и задача сводится к решению равносильной системы:
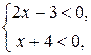 т.е.
т.е. 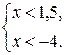
Откуда имеем, что 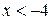 . Итак, получаем ответ:
. Итак, получаем ответ: 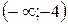 .
.

4. Найти область определения функции:
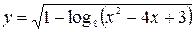 .
.
Решение. Поскольку логарифмическая функция определена только для положительных чисел, а квадратный корень – для неотрицательных чисел, задача сводится к решению системы неравенств:
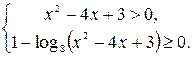
Левую часть первого неравенства разложим на множители, а во втором заменим 1 на 
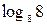 :
:
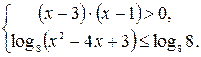
Так как основание логарифма 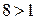 , то, согласно свойствам логарифма, переходим к системе:
, то, согласно свойствам логарифма, переходим к системе:
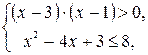 т.е.
т.е. 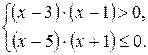
Последняя система равносильна неравенству:
|
|
|
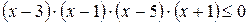 ,
,
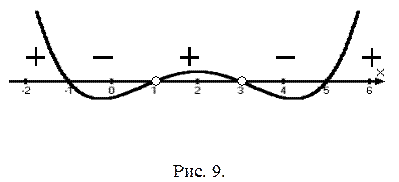
которое решается методом интервалов (причем 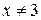 и
и 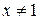 ). С помощью рис. 9 получаем ответ:
). С помощью рис. 9 получаем ответ: 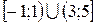 .
.
 2015-01-21
2015-01-21 995
995








