Характерная особенность рассмотренных в предыдущих параграфах матриц состоит в том, что они являются квадратными. Следовательно, они содержат информацию, касающуюся не только двух определенных состояний, но также информацию о любой паре состояний. Часто желательно иметь такую информацию, но она получается ценой выполнения над матрицами трудоемких преобразований, сложность которых возрастает примерно пропорционально квадрату числа состояний автомата. В тех случаях, когда представляют интерес только те пути, которые начинаются из определенного начального состояния, некоторые затруднения, связанные с этими преобразованиями, могут быть обойдены благодаря частичному построению матриц, как это будет показано ниже.
Лемма 2.8. Пусть 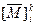 обозначает матрицу-строку, построенную из i -й строки матрицы
обозначает матрицу-строку, построенную из i -й строки матрицы 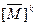 . Тогда
. Тогда
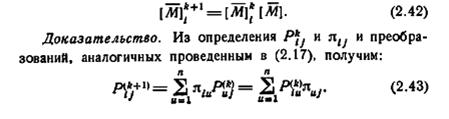
Для фиксированного i множество 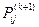 состоит из элементов i-й строки матрицы
состоит из элементов i-й строки матрицы 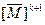 . Также для фиксированного i множество
. Также для фиксированного i множество 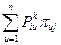 состоит из элементов матрицы-строки, полученной умножением
состоит из элементов матрицы-строки, полученной умножением 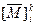 на
на 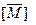 . Следовательно, равенство (2.42) выполняется.
. Следовательно, равенство (2.42) выполняется.
Лемма 2.8 означает, что 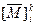 может быть построена путем последовательного умножения
может быть построена путем последовательного умножения 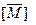 на матрицу-строку, а не на квадратную матрицу. Когда представляют интерес только пути, начинающиеся в σ i, такое частичное построение матрицы оказывается достаточным, так как
на матрицу-строку, а не на квадратную матрицу. Когда представляют интерес только пути, начинающиеся в σ i, такое частичное построение матрицы оказывается достаточным, так как 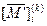 содержит ту же информацию об этих путях, что и вся матрица
содержит ту же информацию об этих путях, что и вся матрица 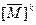 . В результате объем преобразований над матрицами сократится примерно в число раз, равное числу строк в матрице
. В результате объем преобразований над матрицами сократится примерно в число раз, равное числу строк в матрице 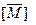 . Можно заметить, что описанная схема частичного построения непосредственно применима к построению матриц
. Можно заметить, что описанная схема частичного построения непосредственно применима к построению матриц 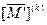 описанному в алгоритме 2.4.
описанному в алгоритме 2.4.
Матрицы (2.44) — (2.47) иллюстрируют схему частичного построения матрицы для определения всех элементарных путей длины 1, 2, 3 и 4, начинающихся в состоянии 1 автомата А1. 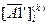 обозначает i-ю строку матрицы
обозначает i-ю строку матрицы 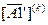 .
.

Можно легко показать, что лемма 2.8 справедлива в случае замены 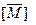 на
на 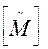 или на
или на 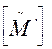 . Поэтому частичное построение можно применять для определения строк скелетных матриц и модифицированных скелетных матриц разных степеней.
. Поэтому частичное построение можно применять для определения строк скелетных матриц и модифицированных скелетных матриц разных степеней.
Задачи
2.1. Постройте таблицу переходов, граф переходов и матрицу переходов для случаев, сформулированных в задачах 1.2—1.9. Для каждого случая рассмотрите число возможных начальных состояний и входных последовательностей и подтвердите, что выходные последовательности, получаемые на основании различных представлений, соответствуют тем, которые предполагались соответствующими словесным описаниям.
2.2. Известно, что конечный автомат имеет входной алфавит {α, β}, выходной алфавит {0,1} и множество состояний {1,2,3}. Начертите граф переходов, удовлетворяющий этим условиям.
2.3. Подсчитайте число различных: (а) (n, p, q)-автоматов, в которых реакция в настоящий момент зависит только от состояния в настоящий момент и не зависит от входного сигнала в настоящий момент; (б) (n, p, q)-автоматов, в которых n = p и из каждого состояния можно перейти в любое другое, подав на автомат один входной символ; (в) (n, p, q)-автоматов, в которых нет изолированных состояний; (г) (n, p, q)-автоматов, в которых каждый из q выходных символов появляется в таблице переходов, по крайней мере, один раз (достаточно получить рекуррентную формулу для подсчета этого числа автоматов).
2.4. Постройте автомат, изоморфный автомату, изображенному таблицей 3 2.1, посредством замены обозначений состояний 1, 2, 3,
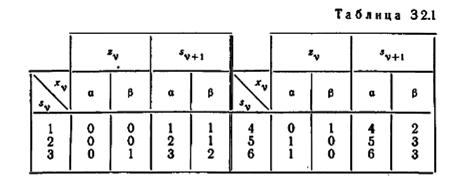
4, 5 и 6 на 2, 3, 4, 5, 6 и 1 соответственно. Без построения всего семейства перестановок автомата покажите, что это семейство имеет мощность, равную 6!.
2.5. Покажите, что если b обозначает число дуг в графе переходов (n, p, q)-автомата, то n ≤ b ≤ np.
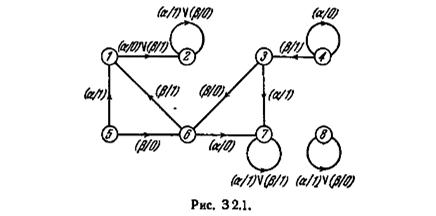
2.6. (а) Постройте таблицу переходов и матрицу переходов автомата, изображенного на рис. 3 2.1. (б) Определите преходящие, тупиковые и изолированные состояния в автомате, (в) Определите для этого автомата G (1), G (2),..., G (8).
2.7. Пусть σ i; — состояние из множества состояний S автомата М. Пусть G (σ i) — σ i -достижимое множество и пусть множество G' (σ i) состоит из элементов множества S, не содержащихся в G (σ i).
Покажите, что: (а) если G' (σ i) ≠ О и G (σ i)∩ G(G' (σ i)) = 0 [16], то G (σ i) и G' (σ i) представляют собой два изолированных подавтомата автомата М; (б) если G' (σ i) ≠0 и G (σ i) ∩ G (G' (σ i)) = 0, то G (σ i)
и G' (σ i) представляют тупиковый и преходящий автоматы соответственно; (в) если G' (σ i) =0, то М не содержит изолированных подавтоматов.
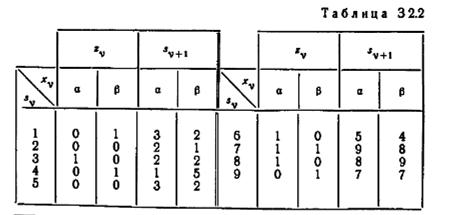
2.8. Таблица 3 2.2 представляет автомат А. (а) Найдите G (5,6) для автомата А. (б) Используя результаты задачи 2.7, покажите, что G (6) представляет изолированный подавтомат, a G (2) — тупиковый подавтомат, (в) Найдите максимальное разложение автомата А.
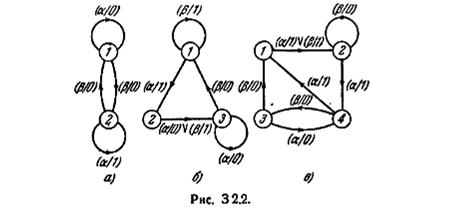
2.9. Постройте таблицу переходов для расщепляемого автомата, который состоит из автоматов А, Б и В, изображенных на рис. 3 2.2.
2.10. Пусть F k (S i) — множество всех состояний автомата М, из которых можно попасть в любое состояние множества S i при подаче входных последовательностей длины k или меньше.
(а) Сформулируйте алгоритм для определения F (S i)-множества состояний, из которых S i достижимо при подаче входной последовательности любой длины, (б) Примените алгоритм к автомату А из задачи 2.8 при S i = {3}. (в) Покажите, что G (S i) U F (S i) = H (S i).
2.11. Автомат A определен матрицей переходов [А], (а) Определите преходящие, тупиковые и изолированные состояния автомата А. (б) Определите G1 (5, 7) и H1(2, 3). (в) Путем изменения порядка строк и столбцов в [А] определите, составляют ли множества состояний {1,2,4,7} и {3,5,6,8} пару из преходящего и тупикового подавтоматов, пару изолированных подавтоматов или пару автоматов, не принадлежащих ни к одному из указанных типов.

вой элемент в i-й строке матрицы 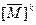 (для любого, целого k≥1) (б) Покажите, что если
(для любого, целого k≥1) (б) Покажите, что если 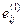 — единственный ненулевой элемент в j-м столбце матрицы
— единственный ненулевой элемент в j-м столбце матрицы 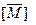 , то
, то 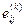 — единственный ненулевой элемент в j-м столбце
— единственный ненулевой элемент в j-м столбце 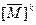 (для любого целого k≥1).
(для любого целого k≥1).
2.13. Покажите, что 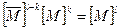 (для всех k≥1).
(для всех k≥1).
2.14. Для автомата А из задачи 2.11 постройте: (а) 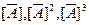 ; (б)
; (б) 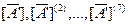 ; (в)
; (в) 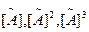 ; (г)
; (г) 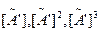 (д) установите, что А не имеет полных контуров.
(д) установите, что А не имеет полных контуров.
2.15. Покажите, что необходимым условием существования полного контура в автомате М является наличие в каждой строке и в каждом столбце матрицы [М], по крайней мере, одного недиагонального ненулевого элемента. Докажите с помощью примера, что это условие не является достаточным.
2.16. Подсчитайте число различных скелетных матриц и скелетных модифицированных матриц, которые описывают (n, p, q) -автоматы.
2.17. Требуется определить, существует ли в автомате М путь, который ведет из σ i в σ k через σ j, и если существует, то определить длину минимального пути, соответствующего такому переходу. Сформулируйте алгоритм для решения этой задачи.
2.18. На автомат M c n состояниями требуется подать такую входную последовательность, чтобы, начиная из состояния σ i, автомат перешел в состояние σ k через (k — 1) h входных символов (где 2 ≤ k ≤ n) и в состояние σ n через nh символов. Полагая, что элементом (i, j) матрицы 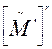 является элемент
является элемент 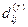 , найдите число возможных последовательностей, которые отвечают сформулированным требованиям.
, найдите число возможных последовательностей, которые отвечают сформулированным требованиям.
2.19. Граф переходов автомата М имеет n состояний, обозначенных σ1, σ2,..., σn, и m дуг, обозначенных β1, β2,..., βm. (n x m)- матрица [Ма] с элементом (i, j), обозначенным через a ij, определяется так:

Покажите, что 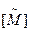 = [Ма] [Mb]t, где [Mb]t является транспонированной матрицей [Мb].
= [Ма] [Mb]t, где [Mb]t является транспонированной матрицей [Мb].
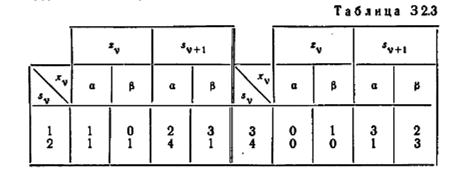
2.20. Используя методику частичного построения матриц, описанную в § 2.13, ответьте на следующие вопросы, относящиеся к автомату, представленному таблицей 3 2.3: (а) Какие кратчайшие входные последовательности переводят автомат из состояния 3 В состояние 1? (б) Какие входные последовательности длины 4 или меньше переводят автомат из состояния 3 снова в состояние 3? (в) Имеет ли автомат полные контуры? Если имеет, то составьте входную последовательность, которая соответствует полному контуру, начинающемуся в состоянии 3.
 2015-02-27
2015-02-27 678
678








