Минимальная x-z-функция

Если известна память µ конечного автомата М, то автомат может быть охарактеризован уравнением вида

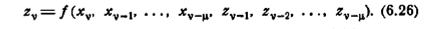
Функцию f, соответствующую выражению (6.26), будем называть x-z-функцией автомата М. Часто x-z-функция содержит целый ряд несущественных переменных и может быть сведена к виду

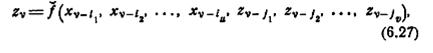
где 0 ≤ i₁ < i₂ <... < i_u, 1 ≤ j₁ < j₂ <... < j_v, а i_u = µ и (или) j _v = µ. Функция f называется минимальной x-z-функцией М, если u + vг»—минимальное число аргументов х_i и z_i, необходимых для выражения z, как функции входных воздействий и выходных реакций в форме (6.27). Таким образом, минимальная x-z-функция получается из x-z-функции путем вычеркивания из последней максимально возможного числа аргументов x_i и z_i. Получение минимальной x-z-функции, или минимизация x-z-функции представляет интерес для целого ряда задач анализа и синтеза, когда для заданного конечного автомата желательна наиболее компактная форма его описания, т. е. форма (6.27).

Задача минимизации x-z-функции может быть сформулирована более точно на языке x-z-таблицы, общая форма которой показана в таблице 6.5.

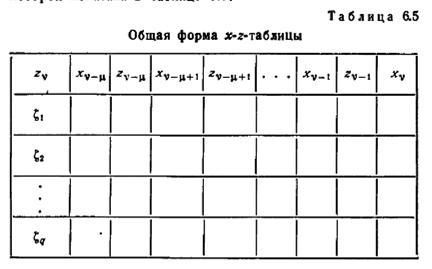
Таблица разделена на q групп строк, по одной группе для каждого выходного символа в выходном алфавите {ζ₁, ζ₂,..., ζ_q} автомата M c n состояниями. Группу строк, обозначенную в столбце z_v символом ζ_k, будем называть ζ_k –гpyппой. Столбцы x_v-µ, z_v-µ, x_v-µ+1, z_v-µ+1,..., x_v-1, z_v-1, x_v заполняются следующим образом. Пусть (ξ_i/ζ_k)является парой вход-выход, связанной с дугой, которая начинается в состоянии σ_i, и пусть (ξ_i1/ζ_k1) (ξ_i2/ζ_k2)... (ξ_iµ/ζ_kµ) -

последовательность вход-выход в множестве Q⁽ⁱ⁾_µ (такие последовательности могут быть получены из таблицы для Q⁽¹⁾_µ, Q⁽²⁾_µ,..., Q^(k)_µ построенной для определения µ по алгоритму 6.1). Тогда последовательность символов ξ _l1, ξ _k1, ξ _l2, ξ _k2,..., ξ _lµ, ξ _kµ, ξ _l (записанная в таком порядке) является строкой ζ_k группы. Следуя этим правилам в отношении всех n состояний, можно заполнить все клетки таблицы. Если число последовательностей в Q⁽ⁱ⁾_µ равно r_i и число,символов вход-входного алфавита равно р, то число строк в x-z-таблице равно 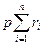. Таким образом x-z-таблица является табличным воспроизведением x-z-функции, в котором значения z_v перечисляются для каждого из тех упорядоченных наборов зна-

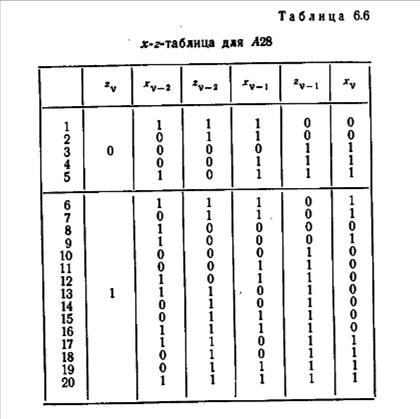
чений (2µ+l) переменных (x_v-µ, z_v-µ, x_v-µ+1, z_v-µ+1,..., x_v-1, z_v-1, x_v), которые могут встретиться в данном автомате. Например, таблица 6.6 является x-z-таблицей автомата A28, показанного на рис. 6.6.

Из матрицы (6.23) видно, что пара вход-выход (0/0) связана с дугой, которая начинается в состоянии 1. Из таблицы 6.4 видно, что множество Q⁽¹⁾₂ состоит из последовательностей вход-выход (1/1) (1/0) и (0/1) (1/0). Следовательно, 0-группа в x-z-таблице должна содержать строки 1,1,1.0,0 и 0,1,1,0,0. Остальные строки в таблице 6.6 заполняются аналогичным образом. Чтобы облегчить последующее изложение материала, придадим строкам и столбцам этой таблицы порядковые номера.

Задача минимизации x-z-функции на языке x-z-таблицы может быть сформулирована следующим образом: вычеркнуть максимальное число столбцов из таблицы так, чтобы ни одна строка любой одной группы не стала одинаковой ни с какой строкой любой другой группы. Пусть столбцами, которые остались после такого вычеркивания, являются x_v-i1, z_v-i2,..., x_v-iu, z_v-j1, z_v-j2,...,z_{v-j v} . Поскольку v+u обязательно является минимальным числом аргументов и поскольку ни один упорядоченный набор значений u + v переменных не появляется в двух различных ζ_k-группах x-z-таблицы, мы имеем:

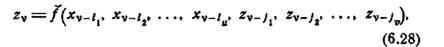
где f—минимальная x-z-функция.

Таким образом, чтобы найти минимальную x-z-функцию, можно воспользоваться следующим алгоритмом.

Алгоритм 6.2. Задана х-z-таблица автомата М. Чтобы определить минимальную x-z-функцию М: (1) Полагаем h = 1. (2) Для каждой комбинации из h столбцов проверяем, делает ли вычеркивание остающихся столбцов строки из различных ζ_k групп одинаковыми. (3) (а) Если каждая комбинация делает строки в различных ζ_k-группах одинаковыми, то увеличиваем h на единицу и возвращаемся к (2). (б) Если есть

комбинация, которая не делает строки в различных ζ_k-группах одинаковыми, то берем эту комбинацию, соответствующую

столбцам x_v-i1, x_v-i2,..., x_v-iu, z_v-j1, z_v-j2,...,z_{v-j v} . Минимальная x-z-функция определяется выражением (6.28).

Выполнение алгоритма 6.2 становится значительно проще, если учесть следующие факты: (1) Каждая рассматриваемая комбинация из h столбцов должна включать либо столбец x_v-µ, либо столбец z_v-µ. (2) Если две строки, принадлежащие двум различным ζ_k -группам, отличаются символами в единственном столбце, то этот столбец включается в каждую рассматриваемую комбинацию из h столбцов. (3) Столбец, который содержит один итот же символ в каждой строке, не должен включаться ни в какую рассматриваемую комбинацию из h столбцов. (4) Два одинаковых столбца вместе не должны включаться ни в какую рассматриваемую комбинацию из h столбцов.

Например, в таблице 6.6 можно заметить, что строки 3 и 18 различаются только значением переменной в столбце 2. Строки 1 и 16 различаются только значением переменной в столбце 4, строки 1 и 6 — только в столбце 5. Следовательно, при применении алгоритма 6.2 столбцы 2, 4 и 5 должны включаться в любую рассматриваемую комбинацию из h столбцов. Проверка строк в этих трех столбцах показывает, что нет такой строки в 0-группе, которая была бы одинаковой с какой-либо строкой в 1-группе. Таким образом, для автомата A28 можно записать:

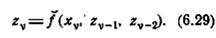
В этом выражении число аргументов минимально.

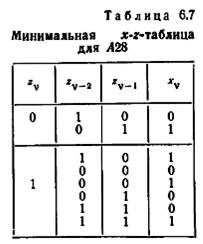
Минимальная x-z-функция может быть представлена в табличной форме путем вычеркивания из x-z-таблицы найденных по алгоритму 6.2 столбцов и объединения всех одинаковых строк. Получаемая в результате таблица называется минимальной х-z-таблицей. Минимальная x-z-таблица для автомата A28 показана в таблице 6.7.

6.6. Линейные двоичные автоматы [37]

В этом и следующих двух параграфах мы будем изучать специальный класс автоматов с конечной памятью, называемых линейными двоичными автоматами, которые вследствие своих интересных и полезных свойств оправдывают повышенное внимание к ним. В линейных двоичных автоматах входным и выходным алфавитами являются {0,1} и выход в любой заданный момент времени равен сумме по модулю 2 значений выбранных входных символов в прошедшие моменты времени (и, возможно, в настоящий момент времени) и выходных символов в прошедшие моменты времени. Обозначив сложение по модулю 2 знаком 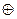, линейный двоичный автомат можно охарактеризовать соотношением

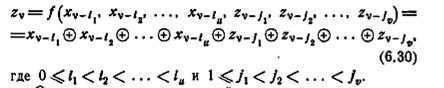
Основное состояние линейного двоичного автомата определяется как состояние автомата, в котором

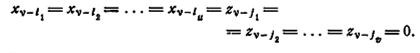
Будем говорить, что автомат находится в покое, если он находится в основном состоянии.

Теорема 6.2. Пусть М есть линейный двоичный автомат,, находящийся в покое в момент времени t₀, и пусть в момент t₀ к автомату М прикладывается входная последовательность х₀ х₁... x_k. Тогда реакция

М в момент t_k (k ≥ 0) определяется выражением

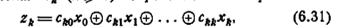
где коэффициенты сы равны либо 0, либо 1.

Доказательство. Пусть автомат М имеет память µ Тогда М может быть охарактеризован уравнением

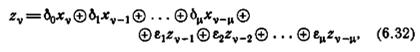
где коэффициенты δ_i и e_i принимают значения 0 или 1. Если М находится в состоянии покоя в момент t₀, то

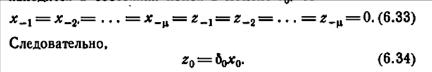
Это равенство доказывает теорему для k = 0. Положим, что теорема справедлива для k=0, 1,..., l. Тогда

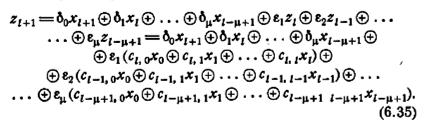
Так как по (6.33) все переменные x_i с отрицательными индексами равны 0, то (6.35) можно записать в виде

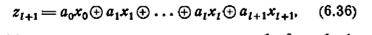
где коэффициенты a _i принимают значения либо 0, либо 1. Следовательно, если теорема справедлива для /k= 0, 1,..., l, то она должна быть справедливой для k = l + 1. По индукции, теорема справедлива для всех k ≥ 0.

Теорема 6.2, в сущности, утверждает, что выходная реакция линейного двоичного автомата, находящегося в состоянии покоя, может быть выражена как линейная комбинация входных воздействий в настоящий и прошедшие моменты времени. Пусть ξ´_i0ξ´_i1...ξ´_ik—входная последовательность, приложенная к двоичному автомату М, находя-

щемуся в состоянии покоя, и пусть ζ´_jk является выходной реакцией автомата М на входное воздействие ξ´_ik. Тогда

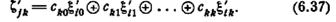
Аналогично пусть — ξ´´_i0ξ´´_i1...ξ´´_ik входная последователь, приложенная к автомату М, находящемуся в состоянии покоя, и пусть ζ´´_jk — реакция автомата М на ξ´´_jk. Тогда

Поэтому линейный двоичный автомат, выведенный из покоя, подчиняется принципу суперпозиции: выходная реакция на сумму (по модулю 2) входных воздействий равна сумме (по модулю 2) выходных реакций на отдельные входные воздействия.

Теперь введем оператор задержки D, определяемый так:

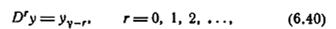
где у может обозначать как х, так и z. Вместо D⁰ будем писать I. В терминах операторов задержки выражение (6.30) может быть записано так:

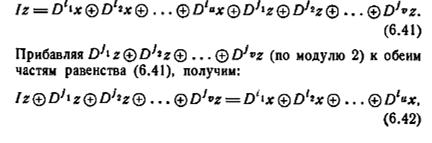
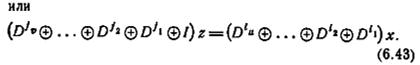
Характеристики вход-выход линейного двоичного автомата М могут быть выражены передаточным отношением, обозначаемым через Т(М):

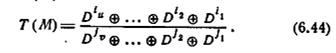
Если задано передаточное отношение автомата, то функция l в том виде, как она представлена равенством (6.30), всегда может быть определена выполнением в обратном порядке операций, описываемых уравнениями (6.41) — (6.44).

Из определения D и равенства (6.41) следует, что

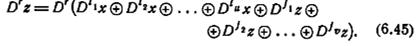
Из (6.45) и свойства суперпозиции следует, что если томат, характеризуемый равенством (6.41), находится в состоянии покоя, то обе части (6.41) могут быть умножены без нарушения равенства на произвольный полином от D:

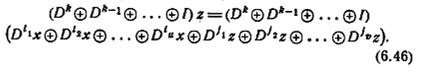
Следовательно, если заданный линейный двоичный автомат М находится в начальный момент времени в состоянии покоя, то числитель и знаменатель его передаточного отношения могут быть умножены на произвольный полином от D. Кроме того, если М находится в начальный момент времени в состоянии покоя и полиномы числителя и знаменателя его передаточного отношения содержат общий множитель, то этот общий множитель может быть без ущерба сокращен. Сокращение общего множителя, которое может быть выполнено с помощью алгоритма Евклида, понижает порядок полиномов числителя и знаменателя в передаточном отношении, тем самым упрощая как анализ, так и синтез рассматриваемого автомата.

Для примера рассмотрим линейный двоичный автомат А29, определенный равенством

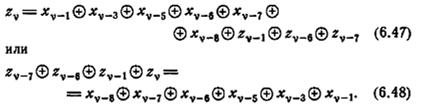
Поэтому передаточное отношение для A29 имеет вид

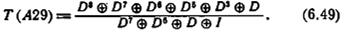
Для того чтобы определить общий наибольший делитель полиномов числителя и знаменателя, применим алгоритм Евклида, заменив вычитание по модулю 2 сложением (и заметив, что

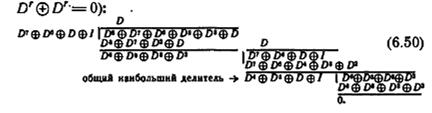
Последний делитель (показанный стрелкой) является общим наибольшим делителем. Для того чтобы понизить передаточное отношение, разделим его числитель и знаменатель на этот делитель:

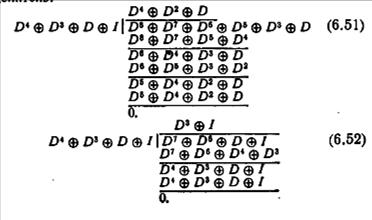
Из (6.51) и (6.52) получаем:

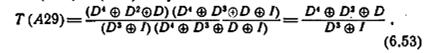
Поэтому работа автоматаA, находящегося в начальный момент времени в состоянии покоя, может быть охарактеризована выражениями

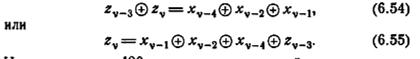
Например, если A29 находится в.начальный момент времени в состоянии покоя, то его выходная реакция на входную последовательность 100111001010 по равенству (6.55) будет 011011010001. Можно легко проверить, что эта выходная реакция совпадает с реакцией, которая получается при первоначальном (более длинном) соотношении (6.47).

В общем случае не все состояния линейного двоичного автомата достижимы из его основного состояния. Когда известно, что автомат находится в основном состоянии, то все состояния, которые недостижимы из этого состояния, могут не учитываться, что приводит к упрощению представления заданного автомата и, следовательно, его анализа. Сокращение общего делителя в передаточном отношении автомата соответствует именно такому упрощению. Автомат, представленный сокращенным отношением, содержит все состояния, достижимые из основного состояния первоначального автомата. Поскольку большинство линейных двоичных автоматов, встречающихся на практике, имеют основное состояние в качестве начального состояния, такое сокращение в большинстве случаев оправдано и желательно.