Свойства автоматов с конечной памятью

Конечный автомат, представляющий систему с конечной памятью, будем называть автоматом с конечной памятью. Таким образом, автомат с конечной памятью М, является автоматом, в котором

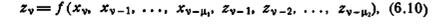
где любой из аргументов (за исключением одного из х₁) может быть несущественной переменной. Числа µ₁ и µ₂ называются соответственно памятью х и памятью z автомата М. Целое число

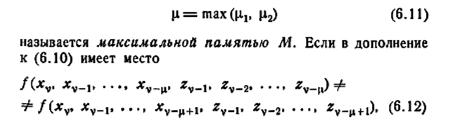
то будем говорить, что автомат М имеет память µ. Таким образом, µ является памятью автомата в том случае, если предсказание выходной реакции, по крайней мере, на одно входное воздействие в момент времени t_v требует знания входного воздействия и (или) выходной реакции в момент времени t_v-µ (и, возможно, входных воздействий и выходных реакций, которые возникают в более поздние моменты времени), но не требует знания каких-либо входных воздействий и выходных реакций в моменты времени более ранние, чем t_v-µ.

В дальнейшем (ξ_i1/ζ_j1)(ξ_i2/ζ_j2)... (ξ_ii/ζ_ji) будем называть последовательностью вход-выход, если входная последовательность ξ_i1 ξ_i2... ξ_ii заставляет автомат генерировать выходную последовательность ζ_j1 ζ_j2... ζ_ji.Будем говорить, что путь в диаграмме переходов описывает последовательность вход-выход (ξ_i1/ζ_j1)(ξ_i2/ζ_j2)... (ξ_ii/ζ_ji), если егo k-я ветвь для k = 1, 2,..., l. обозначена парой вход-выход (ξ_il/ζ_jk) (и, возможно, другими парами вход-выход). Пути будем называть (ξ_i1/ζ_j1)(ξ_i2/ζ_j2)... (ξ_ii/ζ_ji)-совпадающими, если каждый из них описывает последовательность вход-выход

Лемма 6.1. В минимальном автомате с памятью µ

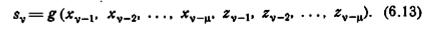
Доказательство. Предположим обратное. Тогда автомат должен содержать по крайней мере два пути, которые являются (ξ_i1/ζ_j1)(ξ_i2/ζ_j2)... (ξ_iµ/ζ_jµ)совпадающими для некоторой последовательности вход-выход (ξ_i1/ζ_j1)(ξ_i2/ζ_j2)... (ξ_iµ/ζ_jµ) и которые оканчиваются двумя различимыми состояниями. Пусть начальные состояния этих путей будут σ_k и σ´_k и конечные состояния — σ_kµ и σ´_kµ; пусть минимальная диагностическая последовательность для σ_kµ и σ´_kµ есть ξi_µ+1 ξi_µ+2... ξi_µ+r (r ≥ 1). Тогда σ_kµ и σ´_kµ дают одинаковые выходные реакции на ξ_i1 ξ_i2... ξ_iµ ξ_iµ+1... ξ_iµ+r-1,. но различные

реакции на ξ_i1 ξ_i2... ξ_iµ ξ_iµ+1... ξ_iµ+r Однако это невозможно, так как по предположению автомат имеет память µ и, следовательно,

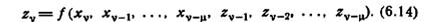
Это равенство означает, что выходная реакция в настоящий момент времени может быть однозначно определена с помощью прошедшей последовательности вход-выход длиной µ. Лемма, таким образом, следует из полученного противоречия.

В дальнейшем будем говорить, что два или более путей пересекаются в состоянии σ_k, если σ_k («пересечение») достижимо из начальных состояний этих путей при одной и той же

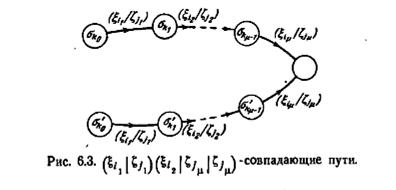
последовательности вход-выход. Лемма 6.1 означает, что диаграмма переходов автомата с памятью µ должна обладать ледующими свойствами. Пути, которые являются (ξ_i1/ζ_j1)X(ξ_i2/ζ_j2)... (ξ_iµ/ζ_jµ)-совпадающими, должны пересекаться в своих конечных состояниях. Кроме того, должна быть, по крайней мере, одна пара (ξ_i1/ζ_j1)(ξ_i“/ζ_j2)... (ξ_iµ/ζ_jµ)- сов падающих путей, которые пересекаются в своих конечных состояниях, но не имеют других пересечений. Такая пара путей показана на рис. 6.3.

Лемма 6.2. Если в заданном автомате М

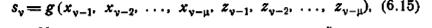
то М является автоматом с максимальной памятью Доказательство. Для любого конечного автомата

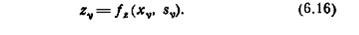
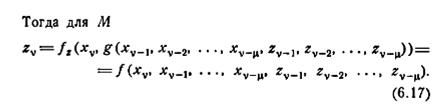
Следовательно, по определению, М является автоматом с максимальной памятью µ.

В связи с предшествующими леммами важно отметить следующее основное различие между произвольным конечным автоматом и автоматом с конечной памятью. В любом конечном автомате имеется, по крайней мере, одна специально составленная входная последовательность (а именно, установочная последовательность), которая, будучи приложенной к автомату, однозначно определяет конечное состояние. В автомате с конечной памятью µ это справедливо для каждой входной последовательности длины µ или больше (независимо от того, специально составлена такая последовательность или нет).

Теорема 6.1. Пусть М-—минимальный автомат с памятью µ и числом состояний n. Тогда

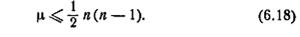
Доказательство. Если автомат М является минимальным и имеет память µ, то должно существовать два пути, которые пересекаются не раньше, чем в своих конечных состояниях, как показано на рис. 6.3. Пусть {σ_ki, σ'_ki } является l -й парой состояний, а { σ_ki+h, σ'_{k l +h} } является (l +h≤µ)-й парой состояний (l +h≤µ) этих путей. Предположим, что совпадают (являются одними и теми же состояниями) σ _kl с σ_ki+h, а также σ´_ki с σ´_ki+h. Тогда два пути, начинающихся в σ_ki и σ´_ki , каждый из которых описывает последовательность вход-выход (ξ_i1/ζ_j1)(ξ_{i l +1} /ζ_{j l +1})... (ξ_il+h-1/ζ_{j l+h-1}) представляют собой замкнутые пути, которые являются (ξ_i1/ζ_j1)(ξ_{i l +1} /ζ_{j l +1})... (ξ_il+h-1/ζ_{j l+h-1}) -совпадающими, и, следовательно, пути бесконечной длины, которые описывают одну и ту же после-

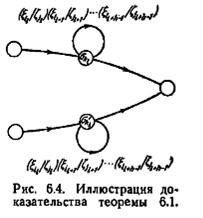
довательность вход-выход, но не пересекаются, (рис. 6.4). По лемме 6.1 такие пути.не могут существовать в автомате с конечной памятью. Теперь предположим, что ок совпадает с σ'_ki+h, а σ'_ki с σ_ki+h.. Тогда начинающиеся в σ_ki и σ´_ki пути, каждый из которых описывает последовательность вход-выход (ξ_{i l} /ζ_{j l} )(ξ_{i l +1} /ζ_{j l +1})... (ξ_{i l +h-1}/ζ_{j l +h-1}) (ξ_{i l} /ζ_{j l} )... (ξ _{il +h-1}/ζ_{j l +h-1}) представляют собой замкнутые пути, которые являются (ξ_{i l} /ζ_{j l} )(ξ_{i l +1} /ζ_{j l +1})... (ξ_{i l +h-1}/ζ_{j l +h-1}) (ξ_{i l} /ζ_{j l} )... (ξ _{il +h-1}/ζ_{j l +h-1})-совпадающими, и, следовательно, пути бесконечной длины, которые описывают одну и ту же последовательность вход-выход, но не пересекаются (рис. 6.5). Снова, по лемме 6.1, такие пути не могут существовать. Таким образом, неупорядоченная l-я пара {σ_kl, σ´_kl}

и неупорядоченная (l +h)-я пара {σ_ki+h, σ'_ki+h } не могут быть совпадающими неупорядоченными парами. Поэтому длина µ любого из путей, показанных на рис. 6.3, не может превышать число неупорядоченных пар состояний, которые могут быть выбраны в автомате с n состояниями. Это число равно

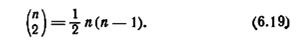
Отсюда следует соотношение (6.18),