Автомат с конечной памятью, в котором z-память равна 0, называется не зависящим от выхода автоматом. Такого типа автомат определяется соотношением
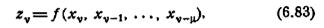
где любой из аргументов может быть несущественным. Не зависящие от выхода автоматы, составляющие подкласс класса автоматов с конечной памятью, проявляют все свойства, полученные ранее для класса автоматов с конечной памятью. В частности, из леммы 6.1 имеем:
Теорема 6.4. В минимальном не зависящем от выхода автомате с памятью µ
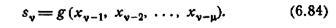
Значит, состояние не зависящего от выхода автомата полностью определяется входной последовательностью длины µ, и, следовательно, такой автомат может непосредственно управляться источником входного возбуждения. Если в автомате М
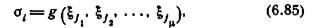
то все, что требуется, чтобы перевести айтомат М в состояние σi, —это подать входную последовательность ξj1ξj2 ... ξjµ. Так как такая последовательность может быть подана на автомат, находящийся в любом состоянии, то из этого следует, что любое состояние в не зависящем от выхода автомате может быть достигнуто из любого другого состояния, а это значит, что не зависящий от выхода автомат эквивалентен сильносвязному автомату.
|
|
|
Пусть задан не зависящий от выхода автомат М с памятью µ и входным алфавитом {ξ1,ξ2,..., ξp}', x-z-функция (6.83) автомата М всегда может быть получена подачей
на вход автомата последовательно всех рµ возможных последовательностей ξj1 ξj2... ξjµ. После определения x-z-функции может быть построена таблица (или граф, или матрица) переходов автомата М. Таким образом, не зависящий от выхода автомат с определенной памятью и входным алфавитом всегда может быть распознан с помощью простого заранее безусловного эксперимента. Заметим, что выходной алфавит не нужен для задания эксперимента, и, следовательно, до эксперимента распознаваемый автомат принадлежит бесконечному классу автоматов. Однако, так как каждый не зависящий от выхода автомат является сильносвязным, то этот класс является исключительным и удовлетворяет условию различимости по теореме 5.3.
Последовательность, которая содержит все рµ возможные подпоследовательности ξj1 ξj2... ξjµ, из µ символов, называется (р, µ) - последовательностью. Самая короткая (р, µ)- последовательность является последовательностью, в которой каждый символ, за исключением последних µ—1 символов, начинает различную подпоследовательность длиной µ. Такая последовательность, длина которой обязательно pµ + µ — 1, называется компактной (р, µ) -последовательностью.
Следующий метод, который будет дан без доказательств, может быть использован для построения компактных (р, µ) -последовательностей для каждого заданного р и µ[38].
|
|
|
Алгоритм 6.3. Для того чтобы построить компактную (р, µ)-последовательность для не зависящего от выхода автомата с памятью µ и входным алфавитом (ξj1 ξj2... ξjµ), нужно произвести следующие операции: (1) Пусть ξj1 = ξj2 =... = ξjµ= ξjp. Полагаем k = µ+l. (2) Рассматривая входной алфавит как упорядоченное множество (ξ1 — первый символ, ξ2 — второй символ,..., ξp — p-й символ), полагаем, что символ ξjk имеет наименьший индекс, так что подпоследовательность ξjk-µ+1 ξjk-µ+2... ξjk. нигде не содержится в последовательности ξj1 ξj2... ξjk-1. (3) (а) Если k < pµ+
+µ— 1, то увеличиваем k на 1 и возвращаемся к (2). (б) Если k = pµ +µ-1, то ξj1 ξj2... ξjk является компактной (р, µ)- последовательностью.
В качестве примера (6.86) показывает построение компактной (3.3)-последовательности для не зависящего от выхода автомата с памятью 3 и входным алфавитом (а, β, γ). Последовательные строки показывают подпоследовательности длины 3 (имеется 27 таких подпоследовательностей). Последняя строка показывает суммарную последовательность, длина которой 33 + 3 — 1 = 29.

Последовательности, полученные по алгоритму 6.3, обладают следующим свойством. Если первые рµ символов
разместить по окружности, то каждая последовательность, построенная считыванием рµ + µ — 1 последовательных символов, образует компактную (р,µ) -последовательность (независимо от начального символа и независимо от того, считываются символы по часовой стрелке или против). Поскольку последовательности, построенные путем выбора
различных начальных символов на окружности (но продолжающиеся в одном и том же направлении), обязательно различны, то каждое применение алгоритма 6.3 может дать рµ различных компактных (р, µ)-последовательностей. Число Wp,µ различных компактных (р,µ)-последовательностей дается[39] выражением
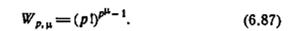
В заключение приведем следующую теорему.
Теорема 6.5. Не зависящий от выхода автомат с известной памятью µ и входным алфавитом мощности р всегда может быть распознан простым безусловным экспериментом длины l, где
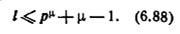
Задачи
6.1. Какие из систем, описанных в задачах 1.2—1.9, представляют системы с конечной памятью? Представьте в виде x-z-таблицы функции тех систем, которые имеют конечную память.
6.2. Покажите, что автомат с нулевой памятью является тривиальным автоматом.
6.3. Постройте таблицу переходов (в минимальной форме) для автомата с конечной памятью, входной и выходной алфавит которого {0,1} и который характеризуется равенством zv = xv-2 X zv-1
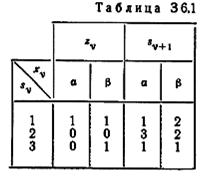
6.4. Автомат, определенный таблицей 3 6.1, имеет память µ. (а) Найдите верхнюю границу µ. (б) Определите µ.
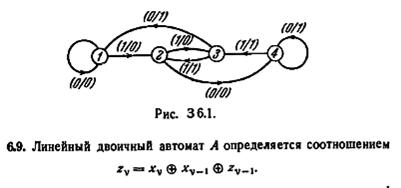
6.5. Для автомата, показанного на рис. 3 6.1: (а) определите память; (б) постройте минимальную x-z-таблицу.
6.6. Покажите, что память минимального (n, р, q)-автомата с конечной памятью не может быть больше, чем (log n)/(log pq).
6.7. Известно, что автомат М имеет р входных символов, n состояний и память µ. Найдите нижнюю границу мощности выходного алфавита.
6.8. Покажите, что длина заданного установочного эксперимента для автомата с памятью µ не превышает µ.
6.9. Линейный двоичный автомат А определяется соотношением
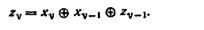
(а) Составьте диаграмму переходов минимального автомата А и определите основное состояние, (б) Найдите передаточное отношение автомата А и упростите его сокращением общего делителя полиномов числителя и знаменателя, (в) Покажите, что автомат А, находящийся в начальный момент времени в состоянии покоя, можно описать соотношением 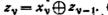 Составьте диаграмму переходов представленного в пункте (в) автомата А, находящегося в начальный момент времени в состоянии покоя. Удостоверьтесь, что этот автомат составляет множество состояний автомата А, которые достижимы из основного состояния, (д) Найдите выходную реакцию автомата А, находящегося в начальный момент времени в состоянии покоя, на входную последовательность 101100011100.
Составьте диаграмму переходов представленного в пункте (в) автомата А, находящегося в начальный момент времени в состоянии покоя. Удостоверьтесь, что этот автомат составляет множество состояний автомата А, которые достижимы из основного состояния, (д) Найдите выходную реакцию автомата А, находящегося в начальный момент времени в состоянии покоя, на входную последовательность 101100011100.
|
|
|
6.10. Линейный двоичный автомат определяется выражением
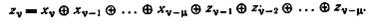
Покажите, что автомат, начинающий работу из своего основного состояния, является тривиальным автоматом.
6.11. (а) Покажите, что D 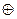 I является делителем Dr
I является делителем Dr 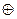 I для любого r ≥ 1. (б) Покажите, что любой полином от D по модулю 2 с четным числом членов имеет делитель D
I для любого r ≥ 1. (б) Покажите, что любой полином от D по модулю 2 с четным числом членов имеет делитель D  I. (в) Покажите, что
I. (в) Покажите, что
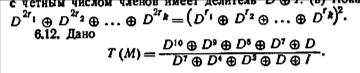
Найдите x-z-функцию для автомата М, находящегося в начальный момент времени в состоянии покоя.
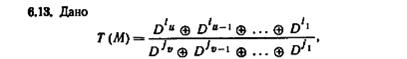
где l u > l u-1 >...> l 1, и jv> jv-1 >...>j1,. (а) Покажите, что T(M) характеризует линейный двоичный автомат, только если j1 ≤i1 (б) Покажите, что если i1=j1=0, то существует автомат M-1, такой, что T(M)T(M-1)= I (т. е. если М и М-1 соединены в каскад, то вход и выход объединенного автомата одинаковы в любой момент времени)[40]. (в) Определите x-z-функцию автомата М-1, если М определяется выражением
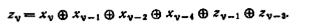
6.14. Покажите, что период свободной выходной последовательности линейного двоичного автомата, имеющего 4 состояния, не может превышать 63.
6.15. На линейный двоичный автомат М с памятью µ подается входная последовательность периода р0. Покажите, что выходная реакция станет периодической после конечного числа символов и что ее период не будет превышать ро(2µ — 1).
6.16. Импульсная характеристика линейного двоичного автомата, из состояния покоя, есть 1011001001001... Найдите выходную реакцию автомата, из состояния покоя, на входные последовательности: (а) 110101000000000..., (б) 101101101101101... Разбейте результирующую выходную реакцию на переходную и периодическую составляющие.
6.17. Импульсная характеристика линейного двоичного автомата, находящегося в состоянии покоя, есть 101010011101001110100111010011... Определите x-z-функцию этого автомата.
6.18. Линейный двоичный автомат определяется выражением
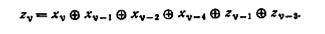
Начальные условия в момент tv: xv-1 = xv-2= xv-3=zv-1 = zv-2 = zv-3=1. Постройте последовательность, которая, будучи приложенной к автомату в момент времени tv, дает постоянный выход, равный 0.
|
|
|
6.19. Известно, что не зависящий от выхода автомат имеет память 5 и входной алфавит {0, 1}. Постройте самый короткий безусловный эксперимент для распознавания автомата.
6.20. Известно, что заданный автомат М является не зависящим от выхода (n, р, q)-автоматом. Покажите, что М может быть
распознан с помощью простого безусловного эксперимента длины l, где
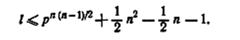
6.21. Постройте автомат с двумя состояниями, отвечающий следующим требованиям: (а) чтобы он не был автоматом с конечной памятью, (б) чтобы он был автоматом с конечной памятью, но не зависящим от выхода, (в) чтобы он был не зависящим от выхода автоматом.
6.22. Показать, что следующие характеристические функции представляют не зависящий от выхода автомат с памятью 1:
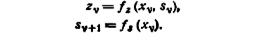
 2015-02-27
2015-02-27 439
439








