Пусть дано конечное множество М; в качестве такого множества можно взять М = {1,2,..,n}.
Определение 1. Биекция j: М ® М называется подстановкой n-ой степени.
Обозначим множество всех подстановок на множестве М через 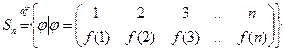 .
.
Докажите самостоятельно, что |Sn| = n!
Определим на множестве Sn операцию композиции двух подстановок (биекций) "xÎM x(j ° y)=(xj)y.
Замечание 1. Из определения следует, что композиция двух подстановок будет снова подставной, т.е. множество Sn замкнуто относительно операции композиции (по теореме о композиции биекций).
Пример 1. Найти композицию двух подстановок:
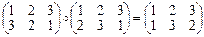 ,
, 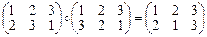 видим, что j ° y ¹ y ° j, т.е. операция (°) некоммутативна.
видим, что j ° y ¹ y ° j, т.е. операция (°) некоммутативна.
Пусть дано множество М={ l,2,..,i,k,...n}.
Запишем одну из перестановок этого множества, например, (1,2,...i, k…n)
Будем говорить, что пара элементов (i, к) образует инверсию, если:
1. i > k.
2. i стоит впереди (слева) от к.
Определение 2. Перестановка называется четной, если в ней четное число инверсий и нечетной, если в ней нечетное число инверсий.
Пример 2. Пусть М = {1,2,3,4,5}, (3,1,4,2,5) одна из его перестановок.
|
|
|
Определим число инверсий в этой перестановке. Для этого поступаем так:
Находим наименьший элемент (это 1), зачеркиваем его и считаем, сколько элементов стоит впереди 1, которые больше 1. Видим, что это одно число 3, затем зачеркиваем двойку и считаем, со сколькими элементами она находится в инверсии и так продолжаем до последнего числа:
1+2+0+0+0=3. Следовательно, перестановка (3.1,4,2,5) - нечетная.
Определение 3. Подстановка j = 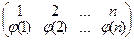 называется четной, если перестановка, стоящая в ее нижней строке, будет четной.
называется четной, если перестановка, стоящая в ее нижней строке, будет четной.
Пример 3. j = 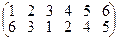 - нечетная (проверьте!)
- нечетная (проверьте!)
Определение 4. Sg n j = 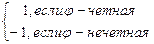
Запись: Sgn j =1 читается так: "знак подстановки j равен 1".
Из определения следует, что Sgn e = 1, действительно, подстановка e = 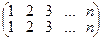 - четная.
- четная.
Sg n j-1 = Sg n j, j-1 = 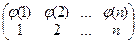
 2015-02-27
2015-02-27 469
469








