2015-02-27
2549
Рассмотрим на примере исследование модели с пятью факторами. Возьмём реплику 25-2. Получаем 8 опытов вместо 32.
Возможны 12 решений, если приравнять х4 парному взаимодействию, а х5 - тройному.
| 1. | х4=х1х2 | х5=х1х2х3 |
| 2. | х4=х1х2 | х5=-х1х2х3 |
| 3. | х4=-х1х2 | х5=х1х2х3 |
| 4. | х4=-х1х2 | х5=-х1х2х3 |
| 5. | х4=х1х3 | х5=х1х2х3 |
| 6. | х4=х1х3 | х5=-х1х2х3 |
| 7. | х4=-х1х3 | х5=х1х2х3 |
| 8. | х4=-х1х3 | х5=-х1х2х3 |
| 9. | х4=х2х3 | х5=х1х2х3 |
| 10. | х4=х2х3 | х5=-х1х2х3 |
| 11. | х4=-х2х3 | х5=х1х2х3 |
| 12. | х4=-х2х3 | х5=-х1х2х3 |
Допустим выбран первый вариант. Тогда определяющими контрастами будут: 1=х1х2х4, 1=х1х2х3х5. Перемножим эти определяющие константы, получим третье соотношение: 1=x3x4x5. Для того чтобы полностью охарактеризовать разрешающую способность реплики, вводят понятие обобщающего определяющего контраста: 1= х1х2х4= x3x4x5=х1х2х3х5.
Система смешивания столбца определяется умножением обобщающего определяющего контраста последовательно на х1,х2,х3:
х1=х2х4=х1х3х4х5=х2х3х5;
х2=х1х4=х2х3х4х5=х1х3х5;
х3 = х1х2х3х4= х4х5х1х2х5;
х4=х1х2=х3х5=х1х2х3х4х5;
х5=х1х2х4х5=х3х4=х1х2х3;
х1х2=х4=х1х2х3х4х5=х3х5.
Если при выбранной реплике некоторые коэффициенты получаются отличными от нуля, например:
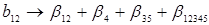
то ставят вторую серию опытов с другой репликой, например берут вариант 4.
Дробные реплики находят широкое применение при получении линейных моделей, причем, целесообразность применения их возрастает с ростом количества факторов. Эффективность применения дробных реплик зависит от выбора системы смешивания линейных эффектов с эффектами взаимодействия.
Планирование экспериментов при построении полной квадратичной модели
В уравнениях (4.28),(4.29),(4.30) учитывались только линейные эффекты и эффекты взаимодействия. В некоторых случаях существенными могут оказаться коэффициенты при квадратных переменных, их кубов и т.д.
Для двухфакторного эксперимента модель может быть представлена выражением
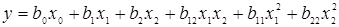(4.33)
Полученные вектор - столбцы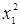 
и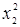 
являются единичными столбцами, совпадающие друг с другом и с фиктивным столбцом 
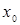. Эти столбцы неразличимы, поэтому нельзя сказать за счет чего получилась величина 
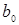. Очевидно она включает в себя значения свободного члена 
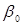и вклады квадратичных членов. Символически это можно записать:
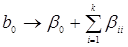
Для квадратичной модели получается следующая система смешивания:
.
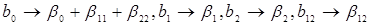Следовательно, планирование эксперимента на двух уровнях не дает возможности получить раздельные оценки коэффициентов при квадратичных членах и фиктивной переменной .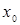
Согласно теории интерполяции, для решения задачи нахождения раздельных оценок число уровней каждой из независимых переменных должно быть на единицу больше степени интерполяционного полинома. Для полинома второй степени число уровней должно быть равно трем.
Однако применение методов ПФЭ плана 3n не является рациональным из-за резкого увеличения опытов эксперимента. Поэтому разработаны специальные методы построения планов второго порядка.
Например, в качестве двухфакторных планов второго порядка могут служить планы, представляемые вершинами и, по крайней мере, одной центральной точкой любого (n-1) мерного правильного многоугольника (который можно вписать в круг).
Пример. Имеем восьмиугольный план (рис.4.11, табл.4.6).
Этот пример можно обобщить на случай получения планов второго порядка. Для этого к ПФЭ типа 2n добавляется центральная точка с координатами (0,0,...0) и, так называемые, звёздные точки с координатами (0,0,...,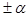 
,...,0), лежащие на сфере диаметра 
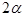. Т.е. план ПФЭ достраивается до плана второго порядка. Такой план называется композиционным планом.
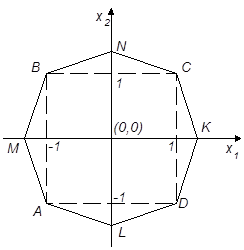
Рис.4.11. Восьмиугольный план эксперимента
Таблица 4.6
| Опыт | x1 | x2 | Описание |
| 1 | -1 | -1 | План 22 |
| 2 | +1 | -1 | представлен |
| 3 | -1 | +1 | квадратом |
| 4 | +1 | +1 | АВСД |
| 5 | Ö2 | 0 | План |
| 6 | -Ö2 | 0 | представлен |
| 7 | 0 | Ö2 | звёздными точками |
| 8 | 0 | -Ö2 | MNKL |
| 9 | 0 | 0 | Центральная точка |
Для трехфакторного эксперимента МПЭ будет иметь следующий вид.
Таблица 4.7
| Опыт | x0 | x1 | x2 | x3 | х12 | х22 | х32 | Описание |
| 1 | +1 | -1 | -1 | -1 | +1 | +1 | +1 |
Продолжение таблицы 4.7
| 2 | +1 | +1 | -1 | -1 | +1 | +1 | +1 | ПФЭ |
| 3 | +1 | -1 | +1 | -1 | +1 | +1 | +1 | |
| 4 | +1 | +1 | +1 | -1 | +1 | +1 | +1 | 22 |
| 5 | +1 | -1 | -1 | +1 | +1 | +1 | +1 | |
| 6 | +1 | +1 | -1 | +1 | +1 | +1 | +1 | |
| 7 | +1 | -1 | +1 | +1 | +1 | +1 | +1 | |
| 8 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | |
| 9 | +1 | -a | 0 | 0 | a2 | 0 | 0 | |
| 10 | +1 | +a | 0 | 0 | a2 | 0 | 0 | Звёздные |
| 11 | +1 | 0 | -a | 0 | 0 | a2 | 0 | |
| 12 | +1 | 0 | +a | 0 | 0 | a2 | 0 | точки |
| 13 | +1 | 0 | 0 | -a | 0 | 0 | a2 | |
| 14 | +1 | 0 | 0 | +a | 0 | 0 | a2 | |
| 15 | +1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 16 | +1 | 0 | 0 | 0 | 0 | 0 | 0 | Центр.нуль.точка |
Добавление двух сфер, образованных звездными точками и центральной точкой, к ПФЭ позволяет получить раздельные оценки b0 и bii. Все три сферы образуют композиционный план второго порядка.
В зависимости от критерия оптимальности плана, различают ортогональное композиционное планирование и рототабельное композиционное планирование.
План, приведенный в табл. 4.6, является рототабельным и обеспечивает получение раздельных оценок b0 и bii.
4.12.1. Ортогональное центральное композиционное планирование
Критерием оптимальности является ортогональность столбцов матрицы планирования. В силу этого свойства все коэффициенты модели определяются независимо друг от друга.
Ортогональность столбцов х0 и хi2 достигается путем преобразования вида:
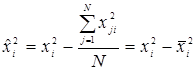(4.34)
С учетом выражения (4.34) условие ортогональности выполняется:
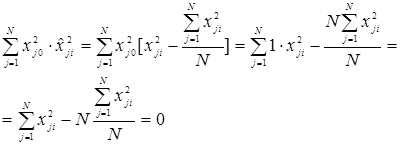
Из условия ортогональности выбирают координату a звездной точки для n - независимых переменных.
Таблица 4.8 соответствует ортогональному композиционному плану для количества переменных n= 2,3,4, где Na - число звездных точек; N0 - число точек в центре эксперимента; Nc - количество точек куба (гиперкуба) при ПФЭ; N - общее число точек факторного пространства.
Таблица 4.8
| n | a | Na | N0 | Nc | N |
| 2 | 1,0 | 4 | 1 | 4 | 9 |
| 3 | 1,215 | 6 | 1 | 8 | 15 |
| 4 | 1,414 | 8 | 1 | 16 | 25 |
Составим матрицу ортогонального планирования для трехфакторного эксперимента. В таблице 4.9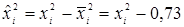 
,
Таблица 4.9
| Номер | x0 | x1 | x2 | x3 |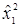 
| 
| 
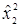
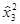
| x1x2 | x1x3 | x2x3 | x1x2x3 |
| опыта | z0 | z1 | z2 | z3 | z4 | z5 | z6 | z7 | z8 | z9 | z10 |
| 1 | +1 | -1 | -1 | -1 | 0,27 | 0,27 | 0,27 | +1 | +1 | +1 | -1 |
| 2 | +1 | +1 | -1 | -1 | 0,27 | 0,27 | 0,27 | -1 | -1 | +1 | +1 |
| 3 | +1 | -1 | +1 | -1 | 0,27 | 0,27 | 0,27 | -1 | +1 | -1 | +1 |
| 4 | +1 | +1 | +1 | -1 | 0,27 | 0,27 | 0,27 | +1 | -1 | -1 | -1 |
| 5 | +1 | -1 | -1 | +1 | 0,27 | 0,27 | 0,27 | +1 | -1 | -1 | +1 |
| 6 | +1 | +1 | -1 | +1 | 0,27 | 0,27 | 0,27 | -1 | +1 | -1 | -1 |
| 7 | +1 | -1 | +1 | +1 | 0,27 | 0,27 | 0,27 | -1 | -1 | +1 | -1 |
| 8 | +1 | +1 | +1 | +1 | 0,27 | 0,27 | 0,27 | +1 | +1 | +1 | +1 |
| 9 | +1 | -1,215 | 0 | 0 | 0,75 | -0,73 | -0,73 | 0 | 0 | 0 | 0 |
| 10 | +1 | +1,215 | 0 | 0 | 0,75 | -0,73 | -0,73 | 0 | 0 | 0 | 0 |
| 11 | +1 | 0 | -1,215 | 0 | -0,73 | 0,75 | -0,73 | 0 | 0 | 0 | 0 |
| 12 | +1 | 0 | +1,215 | 0 | -0,73 | 0,75 | -0,73 | 0 | 0 | 0 | 0 |
| 13 | +1 | 0 | 0 | -1,215 | -0,73 | -0,73 | 0,75 | 0 | 0 | 0 | 0 |
| 14 | +1 | 0 | 0 | +1,215 | -0,73 | -0,73 | 0,75 | 0 | 0 | 0 | 0 |
| 15 | +1 | 0 | 0 | 0 | -0,73 | -0,73 | -0,73 | 0 | 0 | 0 | 0 |
где 1-8 опыт соответствует ПФЭ 23; 9-14 опыт соответствует звездным точкам; 15 опыт - центральная точка.
Анализ результатов экспериментов при ортогональном композиционном планировании имеет некоторые особенности. Так оценки коэффициентов уравнения регрессии находятся с неодинаковой дисперсией.
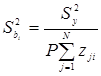(4.35)
Знаменатель выражения (4.35) для разных коэффициентов различен. В формуле (4.35) Р - число параллельных опытов.
Уравнение регрессии для полного квадратичного полинома будет иметь вид:
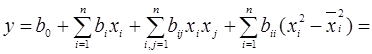
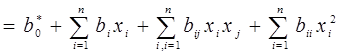, (4.36)
где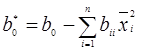 
, n - количество факторов.
Дисперсия коэффициента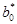 
будет оцениваться по формуле:
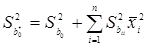(4.37)
Коэффициенты bi, bii и bij определяются по формулам:
, 
, 
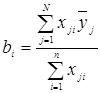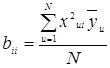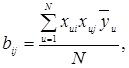
где u =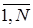 
- число опытов; 
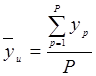, P - число прогонов.
Проверку значимости коэффициентов можно провести по критерию Стьюдента
,
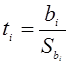где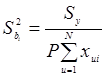 
- дисперсия коэффициента bi.
Проверка адекватности модели проводится по выше изложенной методике с помощью F-критерия Фишера.
Из-за неодинаковой дисперсии коэффициентов регрессии критерий ортогональности является недостаточно сильным критерием оптимальности для планирования второго порядка. Поэтому точность предсказания выходной величины в различных направлениях факторного пространства неодинакова.
Лучшим методом планирования является такой метод, который обеспечивает одинаковую точность во всех направлениях на одинаковом расстоянии от центра. Таким методом является рототабельное композиционное планирование.
4.12.2. Рототабельное композиционное планирование
Критерием оптимальности в рототабельном планировании является условие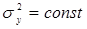 
при одинаковом удалении точек эксперимента от центра, т.е. 
.
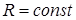Если имеются двухфакторные планы, то, как уже было отмечено, типичными примерами рототабельных планов являются планы, представляемые вершинами и, по крайней мере, одной центральной точкой любого (n-1) - мерного правильного многоугольника, который можно вписать в круг (рис.4.11).
Композиционные центральные рототабельные планы также как и ортогональные состоят из трех сфер: сфера нулевого радиуса - центральные точки; сфера точек куба или гиперкуба и сфера звездных точек. Равномерность расположения точек на сфере приводит к вырожденным матрицам. Для устранения вырожденности используют сферу нулевого радиуса с несколькими центральными точками.
Таблица 4.10
| n | a | Na | N0 | Nc | N |
| 2 | 1,414 | 4 | 5 | 4 | 13 |
| 3 | 1,682 | 6 | 6 | 8 | 20 |
| 4 | 2 | 8 | 7 | 16 | 31 |
где Na - число звездных точек; N0 - число точек в центре эксперимента; Nc - количество точек куба (гиперкуба); N - общее число точек факторного пространства.
Матрица планирования рототабельного плана второго порядка для трехфакторного эксперимента будет представлена в таблице 4.11.
Таблица 4.11
| Номер | x0 | x1 | x2 | x3 | х12 | х22 | х32 | x1x2 | x1x3 | x2x3 |
| опыта | z0 | z1 | z2 | z3 | z4 | z5 | z6 | z7 | z8 | z9 |
| 1 | +1 | -1 | -1 | -1 | +1 | +1 | +1 | +1 | +1 | +1 |
| 2 | +1 | +1 | -1 | -1 | +1 | +1 | +1 | -1 | -1 | +1 |
| 3 | +1 | -1 | +1 | -1 | +1 | +1 | +1 | -1 | +1 | -1 |
| 4 | +1 | +1 | +1 | -1 | +1 | +1 | +1 | +1 | -1 | -1 |
| 5 | +1 | -1 | -1 | +1 | +1 | +1 | +1 | +1 | -1 | -1 |
| 6 | +1 | +1 | -1 | +1 | +1 | +1 | +1 | -1 | +1 | -1 |
| 7 | +1 | -1 | +1 | +1 | +1 | +1 | +1 | -1 | -1 | +1 |
| 8 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 |
| 9 | +1 | -1,682 | 0 | 0 | 2,828 | 0 | 0 | 0 | 0 | 0 |
| 10 | +1 | +1,682 | 0 | 0 | 2,828 | 0 | 0 | 0 | 0 | 0 |
| 11 | +1 | 0 | -1,682 | 0 | 0 | 2,828 | 0 | 0 | 0 | 0 |
Продолжение таблицы 4.11
| 12 | +1 | 0 | +1,682 | 0 | 0 | 2,828 | 0 | 0 | 0 | 0 |
| 13 | +1 | 0 | 0 | -1,682 | 0 | 0 | 2,828 | 0 | 0 | 0 |
| 14 | +1 | 0 | 0 | +1,682 | 0 | 0 | 2,828 | 0 | 0 | 0 |
| 15 | +1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 16 | +1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 17 | +1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 18 | +1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 19 | +1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 20 | +1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Эксперимент проводится аналогично ПФЭ, однако оценки коэффициентов рассчитываются по своим формулам:
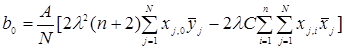(4.38)
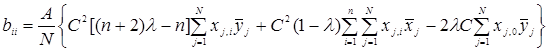(4.39)
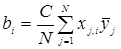(4.40)
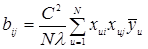(4.41)
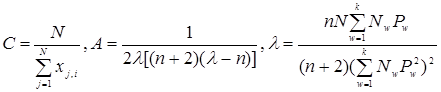(4.42¸4.44)
где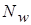 
- число точек на сфере радиуса 
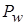; к - число сфер (к=3).
Проводится проверка значимости коэффициентов по t - критерию Стьюдента. Оценки дисперсии и коэффициентов вычисляются по формулам:
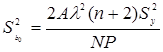(4.45)
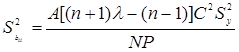(4.46)
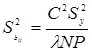(4.47)
Проверка адекватности модели проводится известным методом Фишера.
Рототабельные планы нашли широкое применение на практике. Однако с точки зрения математиков, занимающихся развитием математической статистики, выбор такого критерия представляется мало обоснованным. Он не вытекает логически из тех идей, на которые базируется математика. Например, как выбрать расстояние a до звездных точек; не все пространства независимых переменных, отведенное для эксперимента, используется в композиционных планах и т.д. Невозможно из множества рототабельных планов при одном и том же числе факторов выбрать лучший, т.к. не было критерия оценки. Поэтому этот критерий стали относить к эмпирико-интуитивным критериям.
Наряду с развитием планирования экспериментов, основанных на эмпирико-интуитивным критериях Бокса в США стало развиваться второе чисто теоретическое направление, которое связывают с планом ученого Кифера. Он установил связь между некоторыми критериями оптимальности; теоретически доказал, что для отдельных видов регрессии одни и те же планы могут отвечать сразу нескольким критериям оптимальности.
4.12.3. Разбиение матрицы планирования 2К на блоки
При проведении серии экспериментов, осуществляемых в течение некоторого периода времени или с использованием нескольких партий веществ может произойти изменения условий эксперимента. Для предотвращения смещения среднего уровня отклика точки экспериментального плана рекомендуется выбирать в случайной последовательности. Однако в некоторых случаях влияние внешних условий можно избежать путем подходящего разбиения матрицы на блоки по сырью или последовательности испытаний. Так, при наличии двух партий сырья матрицу 23 можно разбить на два блока таким образом, чтобы эффект сырья сказался на величине трехфакторного взаимодействия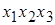 
(табл. 4.12). В этом случае все линейные коэффициенты и парные взаимодействия будут освобождены от влияния неоднородности сырья.
Таблица 4.12
| № блока | x0 | x1 | x2 | x3 | x1x2 | x1x3 | x2x3 | x1x2 x3 | y |
| + | – | – | + | + | – | – | + | 
| |
| + | + | – | – | – | – | + | + | 
| |
| + | – | + | – | – | + | – | + | 
| |
| + | + | + | + | + | + | + | + | 
| |
| + | – | – | – | + | + | + | – | 
| |
| + | + | – | + | – | + | – | – | 
| |
| + | – | + | + | – | – | + | – | 
| |
| + | + | + | – | + | – | – | – | 
|
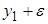
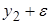
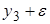
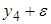
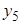
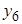
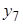
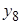
Различие в сырье рассматривают как новый фактор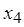 
. Матрица 23, представленная двумя блоками: первый блок 
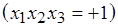и второй блок 
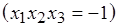, является полурепликой 24-1 с определяющим контрастом 
.
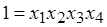Коэффициенты модели будут равны
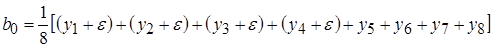
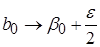
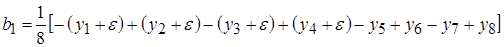
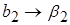
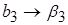
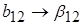
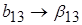
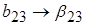
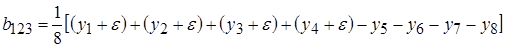
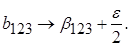
Эффект сырья отразился на подсчете свободного члена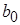 
и коэффициента 
.
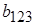Аналогично можно разбить на два блока любой эксперимент 2к. Нужно только выбрать такой элемент взаимодействия, которым можно безболезненно пожертвовать. Обычно, при отсутствии априорных сведений выбирают взаимодействие самого высокого порядка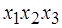 
для 23, 
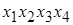для 24, 
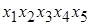для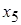 
и т.д.
Если имеется четыре источника неоднородности, которые могут заметно исказить результаты эксперимента, то матрицу 24 разбивают на четыре блока таким образом, чтобы линейные эффекты были освобождены от влияния межблокового эффекта.
Схемы разбиения на блоки рототабельных планов второго порядка так же нужно выполнить с учетом того, чтобы различие между блоками не влияло на коэффициенты при линейных, перекрестных и квадратичных членах. Для того, чтобы не было искажения результатов эксперимента и результаты не зависели от блоковых эффектов число центральных точек должно быть выбрано подходящим образом.
4.13. Критерии оптимальности планов
Минимизацию чувствительности математической модели процесса к случайным факторам проведем с учетом дисперсионных оценок.
Предположим, что вид модели известен. Требуется найти лучшие оценки коэффициентов уравнения регрессии.
Если это уравнение линейное относительно параметров, то оценки уравнений регрессий определяются из системы нормативных уравнений
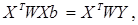
где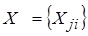 
– матрица независимых переменных; 
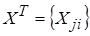– матрица, получаемая транспонированием матрицы 
; 
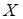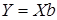– уравнение регрессии в матричной форме; 
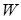– функция веса;
и тогда оценки коэффициентов
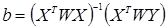
Будем предполагать, что дисперсия выходной величины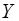 
не зависит от независимых переменных 
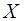и поэтому примем функцию веса 
.
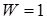С учетом общего вида функциональной зависимости 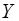от 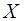получаем следующие оценки:
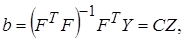(4.48)
где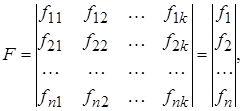 
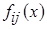- известные функции входных переменных 
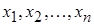, т.е.
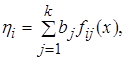(4.49)
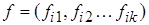. Обозначим 
.
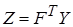Если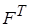 
- транспонированная матрица 
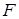, то
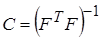(4.50)
– ковариационная матрица. Для линейной модели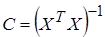 
.
В результате действия случайных факторов экспериментатор получает математическую модель отличную от (4.49):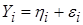 
.
Определим чувствительность решения (4.48) к небольшим изменениям выходной величины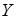 
, а следовательно и 
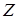за счет случайного фактора:
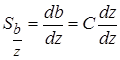(4.51)
Из выражения (4.51) следует, что чувствительность решения "b" по отношению к случайным факторам выражается ковариационной матрицей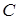 
.
План эксперимента выбирается с учетом минимизации чувствительности решения (4.48) по отношению к случайным воздействиям. Однако в том виде, в каком она предоставлена в выражении (4.51) не представляется возможным дать количественную оценку чувствительности для разных планов 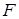. Поэтому в качестве числовой характеристики чувствительности принимают некоторую из числовых характеристик ковариационной матрицы 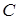. В зависимости от этого получают ряд критериев оптимальности.
1. План называется А–оптимальным, если он минимизирует сумму квадратов главных полуосей эллипсоида рассеяния оценок. Известно, что при нормальном законе распределения результатов наблюдений, поверхностями постоянных значений функции плотности распределения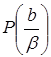 
являются эллипсоиды. Характеристики эллипсоида полностью определяются элементами матрицы 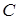. Для двухфакторного эксперимента дадим геометрическую интерпретацию (рис. 4.12)
|
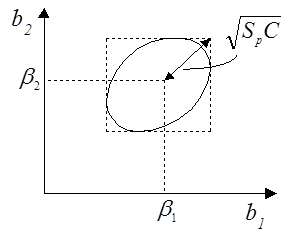
Через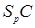 
обозначена сумма диагональных элементов матрицы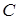
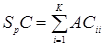
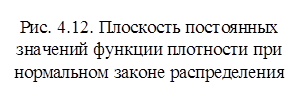На языке матричной алгебры минимизации суммы квадратов главных полуосей эллипсоида означает минимизацию следа (суммы диагональных элементов) ковариационной матрицы уравнения регрессии. Еще можно встретить название минимизация средней дисперсии.
2. План называется D–оптимальным, если он минимизирует величину определителя матрицы 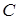. Это соответствует минимизации обобщенной дисперсии.
3. Е–оптимальный план минимизирует максимальную ось эллипсоида рассеяния. Или еще можно назвать минимизацией максимального собственного числа матрицы 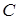или минимизации максимального характеристического значения ковариационной матрицы уравнения регрессии.
4. G–оптимальный план обеспечивает наименьшую по всем планам максимальную величину дисперсии предсказанных значений функции отклика в области факторного эксперимента. Эти планы называют минимаксными.
G –план можно определить из выражения
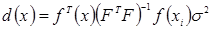(4.52)
План будет G– оптимальным, если
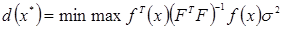(4.53)
Определитель матрицы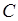 
является наиболее полной числовой характеристикой чувствительности. D– оптимальным план учитывает все элементы матрицы 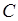. Поэтому он лучше А и Е –оптимальных планов. Что касается G – оптимальным, то он эквивалентен D– оптимальному плану. D– оптимальный план минимизирует объем эллипсоида рассеяния оценок коэффициентов модели.
Таким образом, в качестве числовой характеристики оптимальной оценки модели принимаем определитель матрицы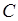
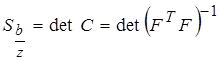(4.54)
Критерием выбора оптимального плана является минимизация чувствительности по всем возможным планам
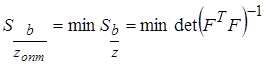(4.55)
т.к. определитель матрицы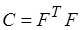 
всегда положителен.
4.14. D–оптимальные планы
4.14.1. Основные свойства D–оптимальных планов
Во многих экспериментах некоторые параметры не интересуют экспериментатора и он их относит к "неизвестным" параметрам. Пусть число интересующих параметров будет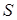 
, а не интересующих 
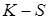. Тогда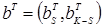 
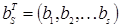– интересующие экспериментатора параметры;
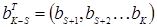– "неизвестные" параметры
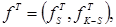
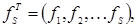
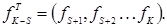
Планы, построенные для подобных случаев, называются "усеченными". Условие D– оптимальности и эквивалентное ему условие G– оптимальности будет иметь вид:
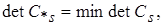(4.56)
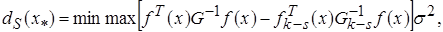(4.57)
где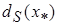 
– дисперсия оценки 
; 
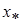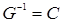, т.е. 
.
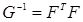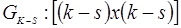– матрица соответствующая "неизвестным" параметрам.
Величина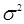 
в выражении (4.57) не влияет на месторасположение максимумов. Для простоты примем 
.
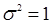Доказано, что для D– оптимального плана при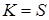 
.
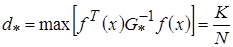. (4.58)
4.14.2. Метод построения D–оптимальных планов
D– оптимальности, требуют большое число наблюдений. Например, при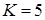 
необходимо было провести более 1000 наблюдений.
В конце 60х годов, построены специальные D– оптимальные планы с достаточно малым числом экспериментальных точек, такие как непрерывные D–оптимальные планы и квази D–оптимальные планы.
Непрерывные D–оптимальные планы связаны с нормированной информационной матрицей, элемент которой записывают следующим образом:
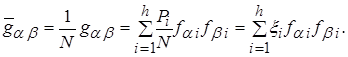(4.64)
Функция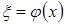 
принимает положительные значения в точках плана и равна нулю во всех остальных точках пространства 
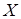. Эту функцию рассматривают как вероятностную меру на пространство 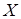. И для того, чтобы план был D– оптимальным нужно выбрать среди всех вероятностных мер на пространство 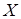, такую меру 
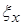, которая бы минимизировала 
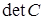. Такие планы называются приближенными или непрерывными. Эти планы можно построить с помощью конечного числа точек пространства планирования и частот повторения наблюдений в этих точках. Такая постановка задачи сильно упрощает построение планов, близких к D– оптимальным.
Рассмотрим более общий случай построения непрерывных D– оптимальных планов. Предлагается производить вычисления по формулам:
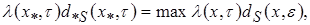(4.65)
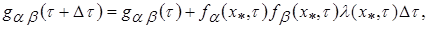(4.66)
где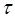 
- время; 
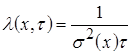– эффективность измерения в точке ; 
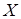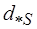– определяется по формуле (4.57); 
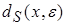– дисперсия точки 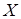в плане 
.
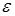Если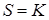 
, то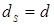 
и тогда 
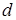определяется по формуле (4.52).
Остановимся на случае 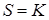. Будем считать, что за время 
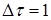проводится только один эксперимент.
Тогда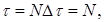 
Кроме того, можно принять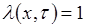 
, т.к., если 
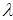будет отличное от единицы, то появляется в левой и правой части выражение (4.65) постоянный коэффициент, который не повлияет на местоположение максимума. Аналогично принимаем за единицу 
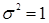. Для рототабельных планов, с учетом сказанного, выражения (4.65) и (4.66) примут вид:
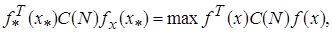(4.67)
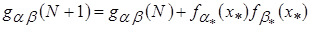(4.68)
