Свойство 1. Значения интегральной функции удовлетворяют двойному неравенству
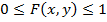
Доказательство. Свойство вытекает из определения интегральной функции как вероятности: вероятность всегда неотрицательное число, не превышающее
единицу.
Свойство 2. F(x, у) есть неубывающая функция по каждому аргументу, т. е.
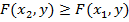 , если
, если 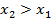 ,
,
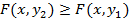 , если
, если 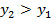 .
.
Свойство 3. Имеет место предельные соотношения:
1) 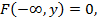
2) 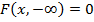 ,
,
3) 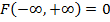 ,
,
4) 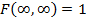 .
.
Свойство 4. а) При 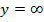 интегральная функция системы становится интегральной функцией составляющей X:
интегральная функция системы становится интегральной функцией составляющей X:
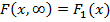 .
.
б) При 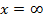 интегральная функция системы становится интегральной функцией составляющей У:
интегральная функция системы становится интегральной функцией составляющей У:
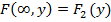 .
.
3.Числовые характеристики двумерной случайной величины.
Дифференциальная функция непрерывной двумерной случайной величины
(двумерная плотность вероятности)
Непрерывную двумерную величину можно также задать, пользуясь дифференциальной функцией распределения. Здесь и далее мы будем предполагать, что интегральная функция всюду непрерывна и имеет всюду (за исключением, быть может, конечного числа кривых) непрерывную смешанную частную производную второгопорядка.
|
|
|
Дифференциальной функцией распределения 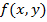 двумерной непрерывной случайной величины (X, Y)называют вторую смешанную частную производную от интегральной функции:
двумерной непрерывной случайной величины (X, Y)называют вторую смешанную частную производную от интегральной функции:
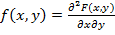 .
.
Геометрически эту функцию можно истолковать как поверхность, которую называют поверхностью распределения.
Условные законы распределения составляющих системы дискретных
случайных величин
Мы установили, что если события А и В зависимы, то
условная вероятность события В отличается от его безусловной вероятности. В этом случае
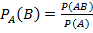 (1)
(1)
Аналогичное положение имеет место и для случайных величин. Для того чтобы охарактеризовать зависимостьмежду составляющими двумерной случайной величины,
введем понятие условного распределения
Рассмотрим дискретную двумерную случайную величину (X,Y). Пусть возможные значения составляющихтаковы
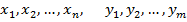
Допустим, что в результате испытания величина У приняла значение 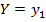 ; при этом X примет одно из своих возможных значении
; при этом X примет одно из своих возможных значении 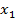 , или
, или 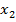 ,..., или
,..., или 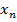 . Обозначим условную вероятность того, что X примет, например значение
. Обозначим условную вероятность того, что X примет, например значение 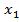 , при условии, что
, при условии, что 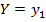 , через
, через 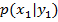 . Эта вероятность, вообще говоря, не будет равна безусловной вероятности
. Эта вероятность, вообще говоря, не будет равна безусловной вероятности 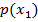 .
.
Условным распределением составляющей X при 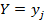 называют совокупность условных вероятностей
называют совокупность условных вероятностей
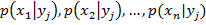 .
.
вычисленных в предположении, что событие 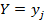 (имеет одно и то же значение при всех значениях X) уже наступило.
(имеет одно и то же значение при всех значениях X) уже наступило.
Аналогично определяется условное распределение составляющей У.
Зная закон распределения двумерной дискретной случайной величины, можно, пользуясь формулой (1), вычислить условные законы распределения составляющих. Например, условный закон распределения X, в предположении, что событие 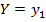 уже произошло, может быть найден по формуле
уже произошло, может быть найден по формуле
|
|
|
 (i =1,2,…, n)
(i =1,2,…, n)
В общем случае условные законы распределения составляющей X определяются соотношением
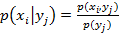 (2)
(2)
Аналогично находят условные законы распределения составляющей У:
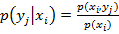 (3)
(3)
Замечание. Сумма вероятностей условного распределения равна единице. Действительно, так как при фиксированном 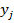 , имеем
, имеем
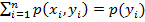 ,
,
то
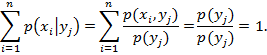
Аналогично доказывается, что при фиксированном 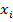
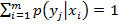 .
.
Это свойство условных распределений используют для контроля вычислений.
 2015-02-27
2015-02-27 1373
1373








