Часто бывает, что для вычисления интеграла 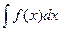 непосредственно подобрать первообразную для f(x) нельзя, но известно, что она существует. Заменим в подынтегральном выражении переменную х некоторой функцией, имеющей непрерывную производную: x = j(t), тогда
непосредственно подобрать первообразную для f(x) нельзя, но известно, что она существует. Заменим в подынтегральном выражении переменную х некоторой функцией, имеющей непрерывную производную: x = j(t), тогда 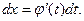 Докажем, что в этом случае имеет место равенство:
Докажем, что в этом случае имеет место равенство:
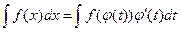 .
.
Здесь подразумевается, что после интегрирования в правой части вместо t будет подставлено его выражение через х, т.е. функция j(t) должна иметь обратную. Для доказательства справедливости последнего равенства покажем, что производные по х левой и правой частей равны между собой, при этом в правой части переменную t считаем промежуточным аргументом сложной функции:
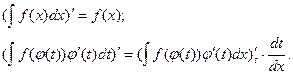
Т.к. зависимость между х и t выражается равенством x = j(t), то по правилу дифференцирования обратной функции имеем:
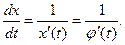
Таким образом, получим:
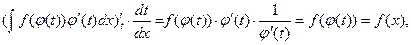 ч.т.д.
ч.т.д.
Пример.
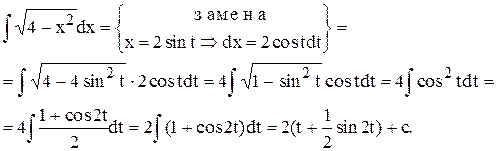
Чтобы “вернуться к старой переменной”, вспомним, что x = 2sint, откуда
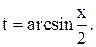 Подставив это выражение в полученное равенство, имеем:
Подставив это выражение в полученное равенство, имеем:
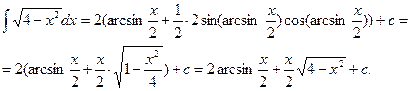
Таким образом, метод замены переменной используется, когда подобрать непосредственно первообразную для функции нельзя.
|
|
|
3. Интегрирование по частям
Среди правил дифференцирования есть правила вычисления производных произведения и частного. Для интегрирования таких общих правил нет, поэтому операция нахождения первообразной - более сложная и творческая, зачастую используются искусственные не всегда очевидные преобразования.
Большое значение имеет метод интегрирования по частям.
Теорема. Пусть u = u(x) и v = v(x) - некоторые дифференцируемые функции.
Тогда: 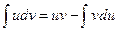 .
.
Доказательство.
Найдем d(uv) = udv + vdu, откуда udv = d(uv) - vdu.
Интегрируя почленно, получим: 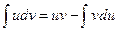 - это выражение называют формулой интегрирования по частям.
- это выражение называют формулой интегрирования по частям.
Во многих случаях эта формула позволяет перейти от сложного интеграла  к более простому
к более простому 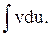
u называют дифференцируемым множителем, т.к. в процессе примене-
ния формулы его приходится дифференцировать; по той же причине dv назы-
вают интегрируемым множителем.
Пример.
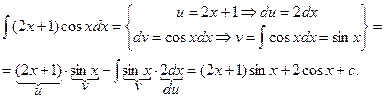
Так как неопределенный интеграл содержит одну произвольную постоянную, то при нахождении функции v по ее известному дифференциалу dv (интегрированием) можно брать одну первообразную.
Таким же способом вычисляются интегралы вида:
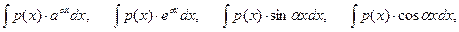 где
где
р(х) - многочлен, a - действительное число, причем здесь за дифференцируемый множитель принимают р(х). При этом формула интегрирования по частям используется столько раз, какова степень многочлена, - например:
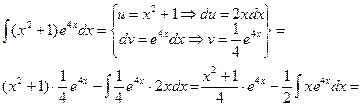
{еще раз по частям}:
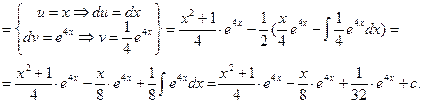

Этим же методом берутся интегралы вида:
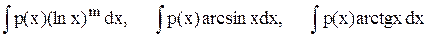
и некоторые другие, причем здесь за dv принимают выражение p(x)dx,
например:
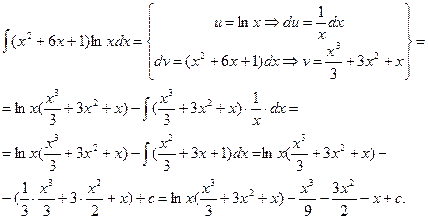
Иногда применение формулы интегрирования по частям приводит искомый интеграл “к самому себе”. В этом случае полученное выражение рассматривают как уравнение относительно исходного интеграла:
|
|
|
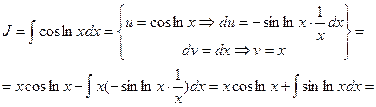
{еще раз по частям}
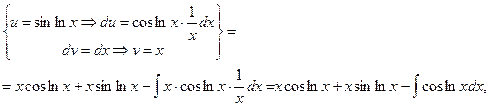
т.е. получили уравнение: 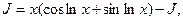
отсюда имеем: 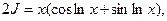
тогда:
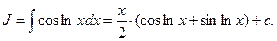
Таким способом можно найти интегралы вида:
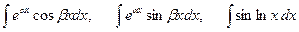 и некоторые другие.
и некоторые другие.
Таким образом, метод интегрирования по частям позволяет производить вычисления сложных интегралов.
 2015-02-27
2015-02-27 435
435







