Первообразная и неопределенный интеграл

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Мы начинаем изучать интегралы, которые широко используются во многих областях техники. Изучение начнем с неопределенного интеграла.

Первообразная и неопределенный интеграл

Основной задачей дифференциального исчисления является дифференцирование данных функций, другими словами, задача нахождения скорости изменения данной функции. Многочисленные вопросы науки и техники приводят к постановке обратной задачи: по заданной функции f (x) восстановить такую функцию F(x), для которой f (x) была бы производной: F^¢(x) = f (x).

Определение. Функция F(x) называется первообразной для f (x), если

F^¢(x) = f (x) или dF(x) = f (x) dx.

Примеры. 1) f (x) = 3x², F(x) = x³;

2) f (x) = cosx, F(x) = sinx.

Легко видеть, что данной функции f (x) = 3x² соответствует не одна первообразная, а множество: х³; х³ + 1; х³ - 1; х³ + 5; х³ - 100; х³ + С.

Действительно, (х³)¢ = 3x²; (x³ + 1)¢ = 3x²; (x³ - 1) ¢ = 3x²;.... (x³ + С)¢ = 3x².

Вообще, если F(x) - первообразная данной функции f (x), то первообразной функцией будет и функция F(x) + c, "СÎR, т.к.:

[F(x) + c]¢ = F¢(x) = f (x).

Исчерпывается ли множество всех первообразных f (x) выражениями вида F(x) + C или же есть первообразные этой функции, не получившиеся из F(x) + C ни при каком значении C? Оказывается, верно утверждение: никаких других первообразных функции f (x) нет. Иными словами, если F₁(x) и F₂(x) - две первообразные для f (x), то F₁(x) = F₂(x) + С,

где С – некоторая постоянная.

Действительно, т.к. F₁ (x) и F₂ (x) - первообразные для f (x), то

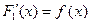и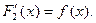

Рассмотрим разность 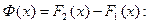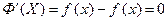при всех х.

Пусть х₀ - какое-нибудь фиксированное значение аргумента,

х - произвольное другое значение.

По формуле Лагранжа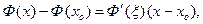

где 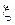- некоторое число между х₀ и х. Так как:

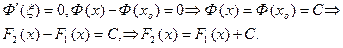
У всякой ли функции f (x) имеется первообразная?

Теорема. Если функция f (x) непрерывна на каком-нибудь промежутке, то она имеет на нем первообразную (без доказательства).

Определение. Если F (x) - какая-то первообразная для f (x), то выражение F (x) + С, где С - произвольная постоянная, называется неопределенным интегралом и обозначается: 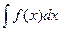, при этом f (x) называется подынтегральной функцией, а выражение f (x) dx - подынтегральным выражением:

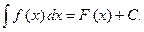
Действие нахождения неопределенного интеграла, иначе, нахождение всех первообразных от данной функции, называется интегрированием этой функции. Очевидно, что операции дифференцирования и интегрирования взаимно обратны.

Сложение и вычитание, возведение в степень и извлечение корня, умножение и деление дают примеры взаимообратных математических операций.

Сделанные друг за другом, они уничтожают результаты друг друга.

1) 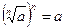; ; 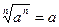a > 0.

2) ln (l^a) = a; l^{ln а} = а; a > 0

То же для операций дифференцирования и интегрирования функций

….; …;

…; ....

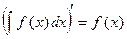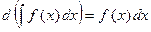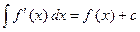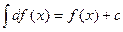Правда, в последних двух формулах появляется постоянное с, но это обстоятельство для многих вопросов не очень существенно.

Таким образом, нахождение неопределенного интеграла есть нахождение всех первообразных от данной функции.