Способ хорд и способ касательных

Эти способы являются наиболее распространенными в случае приближенного решения.

Идея способа хорд состоит в том, что можно с известным приближением допустить, что функция на достаточно малом интервале [а, b] изменяется линейно. Тогда кривую у=ƒ(х) на интервале [а, b] можно заменить хордой и в качестве приближенного значения корня принять точку пересечения хорды с осью абсцисс [7] – рис. (2.1).

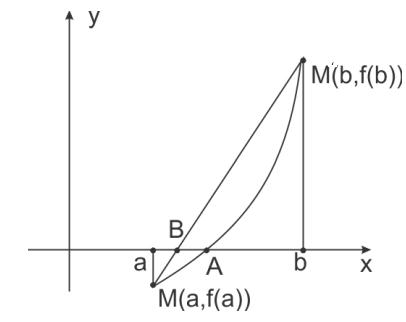
Рис. 2.1

В соответствии с рис. 2.1 истинным корнем уравнения ƒ(х)= 0 является абсцисса точки А, которая представляет собой точку пересечения кривой ММ’ с осью абсцисс. Заменив кривую ММ’ хордой ММ’ мы используем в качестве приближенного значения корня абсциссу точки В, в которой хорда пересекается с осью абсцисс.

Напишем уравнение прямой, проходящей через точки M(a,f(a)) и M’(b,f(b))

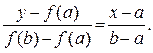(2.2)

Абсцисса точки В, являющаяся приближенным корнем х₁, уравнения ƒ(х) = 0, может быть найдена из уравнения прямой (2.2), если положить в нем у = 0. Тогда будем иметь

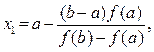(2.3)

или

Уравнение рассматриваемой прямой можно записать и в таком виде

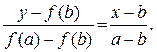
Полагая здесь y = 0, получим

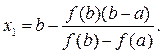(2.4)

Очевидно, формулы (2.3 и (2.4) тождественны. Мы будем пользоваться той из них, которая окажется более удобной.

Полученное значение х₁ можно снова использовать для дальнейшего уточнения корня по способу хорд, рассматривая интервал [ а, x₁ ] или же [ x₁, b ] и исходя из того, в каком из них лежит истинный корень. Чтобы определить это, находят знак ƒ(х₁).

Пример. Найдем по способу хорд положительный корень уравнения

ƒ(х) = x ³ – 2 x ² + 3 x – 5 = 0.

Сначала определим знаки функции в различных точках и результаты сведем в табл. 2.1

Таблица 1

x				1,5	1,8	1,9
ƒ(х1)	–	–	+	–	–	+

Из табл. 2.1 видно, что функция меняет знак на интервале [1, 2]. Однако этот интервал слишком велик. Более узким является интервал [1,8;1,9], к которому мы и применим способ хорд, так как упомянутые выше условия 1) – 3) соблюдены. Вычисление значений данной функции дает

ƒ(1,8) = – 0,248; ƒ(1,9) = + 0,339.

По формуле (2.3) получим

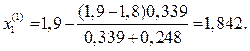
Вычислив значение функции при х = 1,842, находим:

ƒ(1,842) = – 0,01009 < 0. Отсюда видно, что истинный корень расположен в интервале [1,842;1,9]. Снова применив к этому интервалу способ хорд, получим

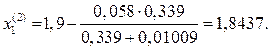
Вычисление значений функции показывает, что

ƒ(1,8437) < 0, ƒ(1,8438) > 0.

Видим, что значение корня находится в интервале между 1, 8437 и 1, 8438. Полагая значение корня равным х= 1,84375, можно утверждать, что погрешность полученного приближения меньше 0,00005.

Перейдем к рассмотрению способа касательных, который называют способом Ньютона. |

Снова обратимся к уравнению ƒ(х) = 0. Введем некоторую точку с интервала [ а, b ] и проведем в точке [ с, ƒ(с) ] заданного графика функции касательную к этому графику – (рис. 2.2).

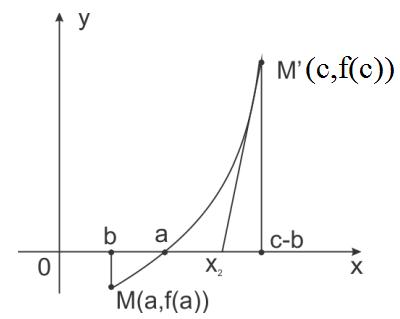
Рис (2.2)

Уравнение касательной имеет вид

y – ƒ(c) = ƒ’(c)(x-c). (2.5)

В качестве приближенного корня уравнения ƒ(x) = 0 примем абсциссу точки пересечения касательной с осью О х.

Уравнение касательной при у = 0, исходя из (2.5), пересекает ось абсцисс в точке

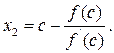(2.6)

На рис. 2.2 мы приняли с = b. Нетрудно видеть, что в этом случае ƒ^’(c) > 0 и ƒ”(с) > 0, так как кривая вогнута. Обычно принимают c = a или с = b, в зависимости от того, в какой из этих точек знак функции совпадает со знаком второй производной, т. е. с выбирают так, чтобы произведение ƒ(c)·ƒ“( c) было положительным. В этом случае можно гарантировать, что приближенное значение корня лежит в интервале [ а, b ], т. е. что а<х₂<b.

Как и в случае применения способа хорд, значение х₂ можно использовать для дальнейшего уточнения значения корня, беря интервал [ a, x₂ ] или [ x₂,b ].

Пример. Рассмотрим то же уравнение, что и в предыдущем случае:

x ³ – 2 x ² + 3 x – 5 = 0

Здесь ƒ '(x) = 3 x ² – 4 x + 3 и ƒ” (x) = 6 x – 4.Из табл. 2.1 выберем интервал [1,8;1,9].Тогда ƒ '(x) > 0 и ƒ” (x) > 0.Если принять с=а, то ƒ (c) ƒ” (c) < 0, так как ƒ (1,8) <0. При с = b = 1,9 имеем ƒ (с)· ƒ "(с) > 0, так что касательную следует проводить в точке с = b.

По формуле (2.6) определяем

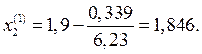
Так как ƒ (1,846) = 0,0132, то в интервале [1,8;1,846] можно вновь применить метод касательных, полагая с = 1,846. Снова используя формулу (2.6), получим

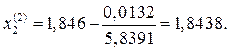
Из полученного результата видим, что погрешность полученного решения не превышает 0,00005.