В ряде случаев более удобным способом решения уравнений является способ итераций (повторений). Для применения этого способа исходное уравнение ƒ(c) =0 нужно представить в форме
х = φ (х) (2.7)
Это всегдаможно сделать, и при том многими способами. Например, уравнение х3 - 2 х - 5 = 0 можно заменить следующими равносильными уравнениями:
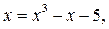
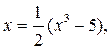
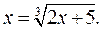
Пусть каким-либо способом выделен интервал [ а,b ], в котором находится значение корня уравнения, и х0 – любая точка этого интервала. Будем считать х0 нулевым приближением. Подставим х0 в правую часть уравнения (2.7) и получим первое приближение
x1 = φ(x0).
Значение х1, снова подставим в уравнение (2.7), получим второе приближение х 2 = φ (х1). Аналогичным способом находим х 3 = φ (х3), х 4 = φ (х4) и т. д. Этот процесс можно продолжать неограниченно, получая последовательность чисел х0, х1, х2,..., хn, … Если эта последовательность имеет предел lim n→∞ хn= х*, то х* является корнем уравнения (2.7). В самом деле предполагая, что φ (х) – непрерывная функция, получим
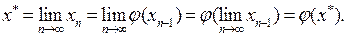
Однако может случится, что последовательность х0, х1, х2,..., хn, … не имеет предела и даже расходится, тогда этот способ не применим.
Представляет большой интерес выяснить условия, при которых итерационный процесс сходится. Эти условия вытекают из следующей теоремы.
Теорема. Пусть интервал [ а, b ] является интервалом, в котором находится только один корень уравнения х = φ(х) и во всех точках этого интервала производная φ’(х) удовлетворяет неравенству.
| φ(х) | ≤ М < 1 (2.8)
Если при этом выполняется условие а ≤ φ(х) ≤ b, то итерационный процесс сходится, причем за нулевое приближение х0 можно взять любую точку интервала [ а, b ].
Пример. Дано уравнение х 3 + 12 х – 2 = 0. Найти один положительный корень. Выделим интервал, в котором содержится один корень. Результаты представим в табл. 2.
Таблица 2
| х | 0,5 | 0,2 | 0,1 | ||
| f (x) | 4,125 | 0,408 | -0,8 |
Из приведенной таблицы следует, чтоуравнение имеет значение корня, заключёное между 0,1 и 0,2. Для уточнения корня применим способ итераций. Представим заданноеуравнение в виде ( 2. 7), что удобно для применения этого способа, а именно:
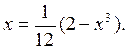 (2.8)
(2.8)
Примемза начальное приближение х0 = 0,16 и будемвычислять последовательные приближения, подставляя ихв(2.8) предыдущие приближенные значения корня. В результате получим:
х 0 = 0,1600,
х 1 = 0,16628 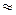 0,1663,
0,1663,
х2 = 0,1663.
Видим, что приближения xt и х2 совпадают. При дальнейшем вычислении будем получать одно и то же число. Поэтому на втором приближении процесс закончим. При возрастании номера члены последовательности приближаются к истинному значению корня 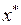 , т.е. полученное приближение является приближенным значением с недостатком. Причем х 2 = 0,1663 есть искомое приближенное значение корняс четырьмя десятичными знаками.
, т.е. полученное приближение является приближенным значением с недостатком. Причем х 2 = 0,1663 есть искомое приближенное значение корняс четырьмя десятичными знаками.
Поясним геометрически способ итераций. Построим на плоскости хОу графики функций у = х и у = φ (х). Каждый действительный корень х * уравнения (2.7) является абсциссой точки пересечения М кривой у = φ (х) с прямой у = х – рис. 2.3.
Отправляясь от некоторой точки А 0 [ х0, φ (х0)], строим ломаную линию А 0 В 1 А 1 В 2 А 2... («лестница»), звенья которой попеременно параллельны оси Ох и Оу. Вершины А 0 А 1 А 2,... лежат на кривой у = φ(х), а вершины В 1, В 2 на прямой y = х. Общие абсциссы точек A 1 и B 1, А 2 и В 2, и т.д., очевидно, представляют собой последовательные приближения x1, x2,... корня х*.
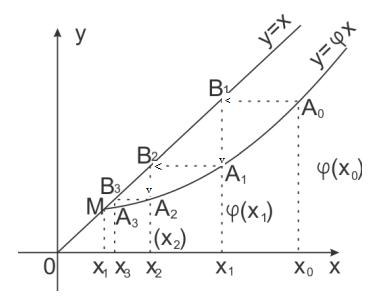
Рис.2.3
Возможен и другой (рис. 2.4) вид ломаной («спираль»). Легко догадаться, что решение в виде «лестницы» получается, если производная φ'(х) положительна, а решение в виде «спирали» - если φ'(х) отрицательна.
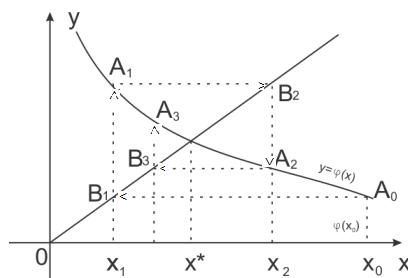
Рис 2.4
На рис. 2.3 кривая у = φ(х) в окрестности корня х* пологая, т. е. | φ'(х)| < 1, и процесс итерации сходится. Однако для случая | φ'(х)| > 1 процесс может быть расходящимся (рис. 2.5).
Итерационный процесс нахождения приближенного значения корня сходится на интервале [ а, b ], если, согласно выше приведенной теореме, выполняются условия (2.8). При этом Оценку погрешности последовательных приближений дает формула
|х* - хп| < (b- а) Мп.
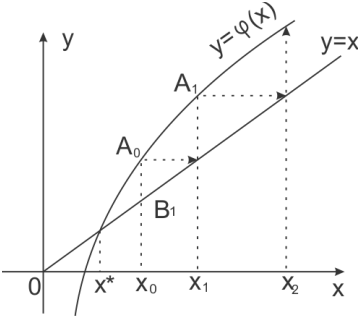
Рис 2.5
 2015-02-04
2015-02-04 1029
1029
