Задача исследовать устойчивость НС по данному методу сводится к нахождению функции Ляпунова и её производной. Функция Ляпунова связана с дифференциальным уравнением системы, записанным для отклонений в форме Коши:
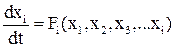 ; (1)
; (1)
где 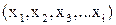 - координаты состояния, Fi – произвольные функции времени (могут быть нелинейными), но должны удовлетворять условию Ляпунова:
- координаты состояния, Fi – произвольные функции времени (могут быть нелинейными), но должны удовлетворять условию Ляпунова:
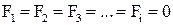 , при
, при 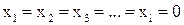
Функция Ляпунова – любая функция вида 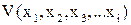 , которая тождественно обращается в 0 при
, которая тождественно обращается в 0 при 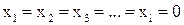 , если в самой функции Ляпунова взяты те же переменные
, если в самой функции Ляпунова взяты те же переменные 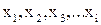 , что и в уравнении системы (1). Она должна быть знакоопределённой и положительной, чтобы её производная по времени тоже была знакоопределённой (или знакопостоянной), но противоположная по знаку самой функции Ляпунова, то система будет асимптотически устойчива.
, что и в уравнении системы (1). Она должна быть знакоопределённой и положительной, чтобы её производная по времени тоже была знакоопределённой (или знакопостоянной), но противоположная по знаку самой функции Ляпунова, то система будет асимптотически устойчива.
З накоопределённая – функция, которая в некоторой области пространства параметров сохраняет во всех точках этой области вокруг начала координат один и тот же знак и нигде не обращается в 0 кроме начальных координат.
Знакопостоянная – функция, которая сохраняет один и тот же знак, но может обращаться в нуль не только в начале координат, но и в других точках данной области.
Пусть функция Ляпунова является знакоопределённой положительной вида:
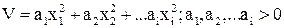
Если задавать функции Ляпунова возрастающие значения от 0 до n, то получим систему уравнений, графическое отображение которых представляет собой поверхности эллипсоидов (первое из уравнений соответствует началу координат).
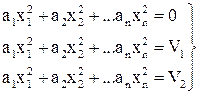
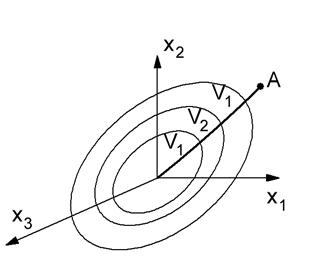
Если производная по времени от функции Ляпунова будет знакоопределённой и отрицательной во всех точках исследуемого пространства, то изображающая точка А будет двигаться в сторону уменьшении функции Ляпунова (V1<V2<V3). В этом случае система, описываемая этой системой уравнений в форме Коши, будет асимптотически устойчива. Если производная по времени от функции Ляпунова будет не знакоопределенная, а знакопостоянная, то в этом случае траектория изображающей точки А не везде будет пересекать поверхности эллипсоидов, а может их касаться в тех точках, где производна будет = 0 (помимо начала координат).
Теорема Ляпунова: Если при заданных уравнениях системы n-го порядка подобрать такую знакоопределённую функцию Ляпунова, что бы её производные по времени была также знакоопределённой, но имела значение противоположное функции Ляпунова, то данная система асимптотически устойчива.
Для того, что бы решить задачу необходимо взять производную по времени от функции Ляпунова:
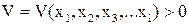 ;
;
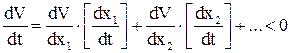 ;
;
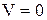 , если
, если 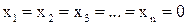
Вместо выражений в квадратных скобках нужно подставить уравнения в форме Коши.
Трудность применения метода Ляпунова для оценки устойчивости состоит в том, что нет общих правил по отысканию функции Ляпунова. При заданных уравнениях системы в общем случае можно подобрать несколько различных вариантов функции Ляпунова, т.к. требуется только её знакоопределённость и положительность. Это может дать различные варианты условий устойчивости для одной и той же системы. Условия, полученные методом Ляпунова, являются достаточными, но могут не охватывать всей области устойчивости системы по параметрам.
Пример:
Пусть свободное движение системы описывается уравнениями:
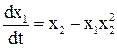
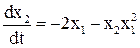
Выберем функцию Ляпунова в виде квадратичной формы 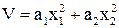 , a1>0 и a2>0, тогда V>0.
, a1>0 и a2>0, тогда V>0.
Производная этой функции:
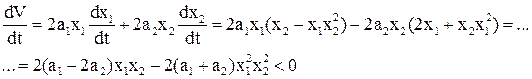
Производная будет знакоопределённой и отрицательной, если 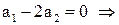
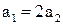 ,
, 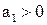
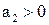 , тогда функция Ляпунова примет вид:
, тогда функция Ляпунова примет вид:
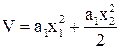 ;
;
Данная функция Ляпунова остаётся знакоопределённой положительной функцией, значит, наша система является асимптотически устойчивой.
 2015-02-04
2015-02-04 617
617








