Прямо и двойственно допустимые «симплекс-таблицы». Правило преобразование «симплекс-таблицы»

Переменные y₁,...,y_m двойственной задачи иногда называют теневыми ценами. Двойственную задачу выгоднее решать, чем прямую, если в прямой задаче при малом количестве переменных имеется большое количество ограничений (m > n).Связь между оптимальными решениями прямой и двойственной задач устанавливают, анализируя следующие теоремы теории двойственности.

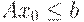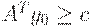Теорема 2.1.1. Если x₀ и y₀ допустимые решения прямой и двойственной задач, то есть и , то

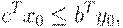
(2.1.17)

то есть значения целевой функции прямой задачи никогда не превышают значения целевой функции двойственной задачи.

Доказательство. Умножим выражение (2.1.12) на 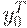, получим

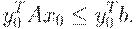
(2.1.18)

Аналогично умножим (2.1.15) на :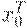

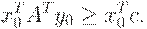
(2.1.19)

Но 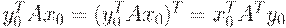, а кроме того .

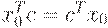Поэтому, сравнивая (2.1.19) и (2.1.18), получим

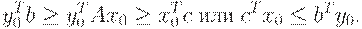Теорема доказана.

В рассматриваемом ниже алгоритме симплекс-метода исполь­зуется так называемая симплекс-таблица, которую следует рас­сматривать как удобную форму записи информации о текущем со­стоянии процесса вычислений. Для построения симплекс-таблицы, соответствующей базису В = [^4<т(1), • • •, ^4<т(т)]) требуется выпол­нить переход от системы уравнений (2.2) к эквивалентной системе

хв + В~1Нх^ = В~1Ь (2.2')

и, используя эту систему для представления базисных перемен­ных через небазисные, исключить базисные переменные из выра­жения целевой функции ио. В результате для целевой функции будет получено представление

ю = свВ-1Ь+ (сдг - свВ-1Х)Х1Ч, (2.Г)

где св = (с<т(1)5 • • ч са(т))^ а CN образован компонентами с^, ] 6 Б1, т.е. коэффициентами при небазисных переменных в исходном представлении целевой функции ио.

Замечание. Функция, задаваемая равенством (2.1'), отличает­ся от исходной целевой функции, если рассматривать их во всем пространстве Кп, но они совпадают на множестве решений систе­мы (2.2), в частности, это совпадение имеет место на множестве

я.

Совместное рассмотрение соотношений (2.1') и (2.2') приводит к следующей системе линейных уравнений

-т + ^2 20]хз = ^оо (2-1") зев'

І Є 5'

(2.2")

где

^оо = -свВ~хЬ, (^ю,..., гт0)т = В~1Ь1 Щ = сз ~ свВ~1 А3, і = 1,...,га, (^1І) • • •) 2т^Т = В 1А,-, _7 = 1,..., п.

(2.4)

Коэффициенты гі3- данной системы, включая также правые части уравнений, и составляют симплекс-таблицу (с некоторыми дополнительными элементами в виде столбца слева от таблицы и строки над таблицей, назначение которых — повысить ее ин­формативность):

— ио	^00	^01	■ ■ щ ■	20п
	^10	211 •
с<т(г)		^г'1		• • ^іп
(т(т)	^т0	^7ПІ	• • ^тз

(2.5)

Характерной особенностью такой таблицы является следую­щее свойство: при любом і = 1,...,т столбец с номером а (і) является единичным вектором, имеющим 1 в г-ж строке и 0 в остальных строках. Таким образом, в случае а [г) = г, г = 1,..., т симплекс-таблица имеет вид

— ги	^00	0.	. 0..	. 0	^От + 1	20п
Х\	^10	1.	. 0..	. 0	21т + 1	21п
х%	^г'О	0.	. 1..	. 0		• • ^гп
Хт	^т0	0.	. 0..	. 1

В новых обозначениях базисное решение ж, соответствующее базису В, имеет вид хв = (^ю, 220, • • •, 2то)Т, ждт = 0, а целевая функция ги на данном решении принимает значение ио(х) = — г^оо-

Определение 2.1 Симплекс-таблица (2.5) называется прямо (двойственно) допустимой, если > О, г = 1,...,то, (zoj > О, ^ = 1,..., га). Базис В, которому эта таблица соответству­ет, также называется прямо (двойственно) допустимым.

Присутствие в названиях слов "прямо"и "двойственно"станет понятным, когда ниже речь пойдет о двойственности в линейном программировании.

Следующее утверждение содержит весьма полезное достаточ­ное условие оптимальности.

Утверждение 2.3 Если симплекс-таблица прямо и двойствен­но допустима, то соответствующее базисное решение являет­ся оптимальным решением задачи (2.1)-(2.3).

Доказательство. Непостредственно из предыдущего определе­ния следует, что соответствующее данной симплекс-таблице ба­зисное решение ж является допустимым решением задачи (2.1)-(2.3). Из двойственной допустимости следует, что целевая функция

зев'

имеет неотрицательные коэффициенты при переменных Ху По­скольку в любом допустимом решении х 6 <5 все переменные име­ют неотрицательные значения, то ги(х) > —^оо = ио(х). Утвер­ждение доказано.Таким образом, из доказанных выше утверждений следует, что при поиске оптимального решения задачи (2.1)-(2.3) мож­но ограничиться рассмотрением базисных допустимых решений. Более того, достаточно найти базис, которому соответствует пря­мо и двойственно допустимая симплекс-таблица. При этом сле­дует однако заметить, что вопрос о существовании такого базиса в случае, когда задача разрешима, остается в данный момент открытым и положительный ответ на него нам еще предстоит получить. Тем не менее по пути поиска прямо и двойственно до­пустимого базиса мы и намерены пойти (именно такой поиск и происходит при решении задачи ЛП симплекс-методом).