Определим передаточную функцию по уравнениям состояния. Рассмотрим систему, которая описывается уравнениями состояния:
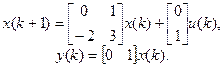
Матрица [z I - A ]-1 была получена в примере 3:
[z I - A ]-1 = 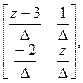 где D = z2 - 3z + 2.
где D = z2 - 3z + 2.
Тогда на основании (26), учитывая, что D = 0, определим передаточную функцию системы:
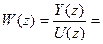 C [z I - A ]-1 B =
C [z I - A ]-1 B = 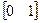

Как видим, этот результат совпадает с передаточной функцией из примера 2. Его можно проверить с помощью программы MATLAB:
A=[0 1;-2 3];
B=[0;1];
C=[0 1];
[Wnum,Wden]=ss2tf(A,B,C,0)
4. Вычисление импульсной переходной функции
Объединим уравнения (17) и (20), положив x (0)=0:
y(k) = 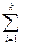 CA i-1 B u(k-i) + D u(k). (28)
CA i-1 B u(k-i) + D u(k). (28)
Пусть входной сигнал имеет вид
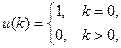
тогда импульсная переходная функция определяется рекуррентной формулой
g(0)=d,
g(k)= CA k-1 B для k>0. (29)
Отсюда можно получить соотношение, связывающее импульсную переходную функцию и z-передаточную функцию
W(z)= 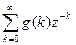 = D +
= D + 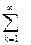 CA k-1 B z-k. (30)
CA k-1 B z-k. (30)
5. Управляемость дискретных САУ
Линейный динамический объект называют управляемым, если существует реализуемая последовательность управляющих воздействий u(k), позволяющая перевести объект из произвольного начального состояния x (0) в любое конечное состояние x (N) на ограниченном интервале времени, равном N тактов квантования.
Для того чтобы получить указанную последовательность u(k), можно воспользоваться уравнением (20). Для объекта со скалярным входом
x (N) = A N x (0) + [ B, AB, …, A N-1 B]u N, (31)
где
u NT = [u(n-1) u(n-2) … u(0)]. (32)
При N=m неизвестный вектор входных воздействий определяется однозначно по формулам
u m = Q s-1[ x (m) – A m x (0)], (33)
Q s = [ B AB…A m-1 B ], (34)
если
det Q s ≠ 0. (35)
Матрица Q s называется матрицей управляемости. Она не должна иметь линейно зависимых столбцов (строк). Следовательно, объект управляем, если выполняется условие
Rank Q s = m, (36)
где m – порядок матрицы A. Если N<m, решения относительно вектора u не существует, а при N>m оно становится неоднозначным.
6. Наблюдаемость дискретных САУ
Линейный динамический объект с выходной переменной y(k) называют наблюдаемым, если произвольное состояние x (k) можно определить, имея конечный набор выходных переменных y(k), y(k+1),…,y(k+N-1). Условия наблюдаемости выведем следующим образом.
Воспользовавшись уравнением выхода
y(k) = Cx (k)
и векторным разностным уравнением (16), сформируем последовательность уравнений
y(k) = Cx (k),
y(k+1) = CAx (k) + CB u(k),
y(k+2) = CA 2 x (k) + CAB u(k) + CB u(k+1),
…..
…..
…..
y(k+N-1) = CA N-1 x (k) + [0, CB, CAB, …, CA N-2 B ]uN. (37)
Здесь
u NT = [u(k+N-1)…u(k+1) u(k)]. (38)
Если все составляющие вектора входных воздействий u NT известны, для однозначного определения m неизвестных, образующих вектор состояния x (k), из системы (37) достаточно взять m уравнений. Таким образом, N=m. При этом систему (37) можно записать в виде
y m = Q B x (k) + Su m, (39)
где
y mT = [y(k) y(k+1) … y(k+m-1)],
u mT = [u(k+m-1) … u(k+1) u(k)],
Q B = [ C CA … CA m-1]T,
S = 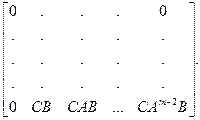
Отсюда найдём искомый вектор состояния
x (k) = Q B-1[ y m – Su m]. (40)
Решение существует, если det Q B ≠ 0. Следовательно, динамический объект наблюдаем, если его матрица наблюдаемости Q B имеет полный ранг
Rank Q B =m, (41)
т.е. все m строк (столбцов) матрицы Q B должны быть линейно независимы.
 2015-02-04
2015-02-04 1090
1090
