Свободные колебания (собственные колебания) - колебания в любой колебательной системе, происходящие в отсутствие внешнего воздействия.
Дифференциальное уравнение свободных колебаний системы с одной степенью свободы:
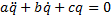 , где a>0; b
, где a>0; b 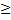 0; c>0.
0; c>0.
а - обобщенный коэффициент инерции; b - обобщенный коэффициент сопротивления; с - обобщенный коэффициент жесткости.
В случае если система консервативная, т.е. b=0, дифференциальное уравнение движения принимает форму:
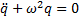 , где
, где 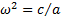 - круговая или циклическая частота.
- круговая или циклическая частота.
Запишем дифференциальное уравнение в виде:
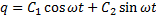 .
.
C1 и C2 - произвольные постоянные, которые мы определим из начальных условий: при t=0 q=q0, 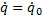 .
.
Отсюда C1=q0; 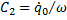 .
.
Введем новые произвольные постоянные:
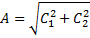 ;
; 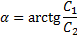
и представим решение дифференциального уравнения в амплитудной форме:
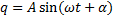 .
.
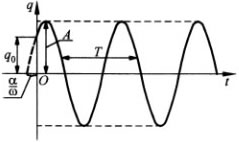
Амплитуда (А) - наибольшее отклонение какой либо точки тела, совершающего колебания, от положения равновесия.
Произвольные постоянные А и α выражаются через начальные условия следующим образом:
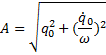 ;
; 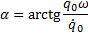 .
.
Зависимость q(t) представлена на рисунке.
|
|
|
Гармонические колебания - колебания, при которых обобщенная координата изменяется во времени по закону синуса или косинуса.
Свободные колебания с одной степенью свободы являются гармоническими.
Характеристики гармонических колебаний:
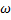 - круговая, или циклическая частота, измеряемая в секундах в минус первой степени;
- круговая, или циклическая частота, измеряемая в секундах в минус первой степени;
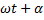 - фаза колебаний;
- фаза колебаний;
Фаза колебаний - физическая величина, при заданной амплитуде и коэффициенте затухания, определяющая состояние колебательной системы в любой момент времени, или проще: аргумент синуса.
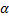 - начальная фаза колебаний;
- начальная фаза колебаний;
А - амплитуда колебаний;
Т - период колебаний - время в секундах. за которое фаза колебаний изменится на 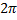
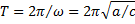 .
.
В инженерной практике используют величину, обратную периоду колебаний, называемую частотой колебаний
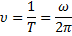
и измеряемую в герцах (Гц).
Круговая частота 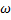 , период колебаний Т и частота
, период колебаний Т и частота 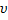 не зависят от начальных условий, поэтому их называют собственными характеристиками колебательной системы.
не зависят от начальных условий, поэтому их называют собственными характеристиками колебательной системы.
Свойство независимости частоты и периода колебаний от начальных условий - свойство изохронности колебаний - связано с линейностью дифференциального уравнения и, следовательно, с допущением о малости колебаний.
Частота n — число полных колебаний за единицу времени. В СИ измеряется в герцах (Гц). Частота колебаний равна одному герцу, если за 1 секунду совершается 1 полное колебание. 1 Гц= 1 с-1.
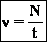
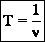
Амплитуда - наибольшее смещение от положения равновесия. Если колебания незатухающие, то амплитуда постоянна.
Фаза колебания - φ - физическая величина, определяющая смещение x в данный момент времени. Измеряется в радианах (рад). Фаза колебания в начальный момент времени (t=0) называется начальной фазой (φ0).
|
|
|
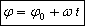
Изохронность колебаний (др.-греч. ἴσος «равный» + χρόνος «время») — физический термин, обозначающий независимость периода собственных колебаний колебательной системы от амплитуды этих колебаний. Колебания, период которых не зависит от амплитуды называют изохронными колебаниями.
Изохронность колебаний — одно из типичных свойств линейных систем, но в случае, если эти колебания имеют малые амплитуды, изохронность соблюдается и в нелинейных системах: к примеру, колебания реального маятника, в общем случае описываемые нелинейным законом, часто считаются изохронными, если амплитуда его угловых отклонений достаточно мала.
Изохронность колебаний системы позволяет линеаризовать её математическое описание и существенно упростить решение. Многие учебные задачи содержат замечания, позволяющие считать системы изохронными и, таким образом, описывать их линейными уравнениями.
Колебания, совершающиеся под воздействием внешней периодической силы, называются вынужденными.
В этом случае внешняя сила совершает положительную работу и обеспечивает приток энергии к колебательной системе. Она не дает колебаниям затухать, несмотря на действие сил трения.
Периодическая внешняя сила может изменяться во времени по различным законам. Особый интерес представляет случай, когда внешняя сила, изменяющаяся по гармоническому закону с частотой ω, воздействует на колебательную систему, способную совершать собственные колебания на некоторой частоте ω0.
Если свободные колебания происходят на частоте ω0, которая определяется параметрами системы, то установившиеся вынужденные колебания всегда происходят на частоте ω внешней силы.
После начала воздействия внешней силы на колебательную систему необходимо некоторое время Δt для установления вынужденных колебаний. Время установления по порядку величины равно времени затухания τ свободных колебаний в колебательной системе.
В начальный момент в колебательной системе возбуждаются оба процесса – вынужденные колебания на частоте ω и свободные колебания на собственной частоте ω0. Но свободные колебания затухают из-за неизбежного наличия сил трения. Поэтому через некоторое время в колебательной системе остаются только стационарные колебания на частоте ω внешней вынуждающей силы.
Рассмотрим в качестве примера вынужденные колебания тела на пружине (рис. 2.5.1). Внешняя сила 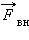 приложена к свободному концу пружины. Она заставляет свободный (левый на рис. 2.5.1) конец пружины перемещаться по закону
приложена к свободному концу пружины. Она заставляет свободный (левый на рис. 2.5.1) конец пружины перемещаться по закону
y = ym cos ωt.
где ym – амплитуда колебаний, ω – круговая частота.
Такой закон перемещения можно обеспечить с помощью шатунного механизма, преобразующего движение по окружности в поступательно-возвратное движение (рис. 2.5.1).
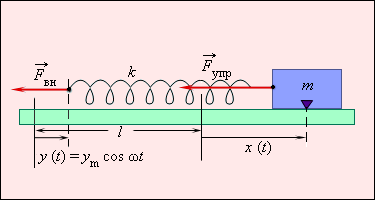
Рисунок 2.5.1. Вынужденные колебания груза на пружине. Свободный конец пружины перемещается по закону y = ym cos ωt. l – длина недеформированной пружины, k – жесткость пружины
Если левый конец пружины смещен на расстояние y, а правый – на расстояние x от их первоначального положения, когда пружина была недеформирована, то удлинение пружины Δl равно:
Δl = x – y = x – ym cos ωt.
Второй закон Ньютона для тела массой m принимает вид:
ma = –k(x – y) = –kx + kym cos ωt.
В этом уравнении сила, действующая на тело, представлена в виде двух слагаемых. Первое слагаемое в правой части – это упругая сила, стремящаяся возвратить тело в положение равновесия (x = 0). Второе слагаемое – внешнее периодическое воздействие на тело. Это слагаемое и называют вынуждающей силой.
Уравнению, выражающему второй закон Ньютона для тела на пружине при наличии внешнего периодического воздействия, можно придать строгую математическую форму, если учесть связь между ускорением тела и его координатой: 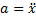 Тогда уравнение вынужденных колебаний запишется в виде
Тогда уравнение вынужденных колебаний запишется в виде
|
|
|
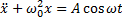 (**)
(**)
где 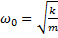 – собственная круговая частота свободных колебаний, ω – циклическая частота вынуждающей силы. В случае вынужденных колебаний груза на пружине (рис. 2.5.1) величина A определяется выражением:
– собственная круговая частота свободных колебаний, ω – циклическая частота вынуждающей силы. В случае вынужденных колебаний груза на пружине (рис. 2.5.1) величина A определяется выражением:
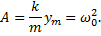
Уравнение (**) не учитывает действия сил трения. В отличие от уравнения свободных колебаний уравнение вынужденных колебаний (**) содержит две частоты – частоту ω0 свободных колебаний и частоту ω вынуждающей силы.
Установившиеся вынужденные колебания груза на пружине происходят на частоте внешнего воздействия по закону
x (t) = xmcos (ωt + θ).
Амплитуда вынужденных колебаний xm и начальная фаза θ зависят от соотношения частот ω0 и ω и от амплитуды <m>m>ym внешней силы.
На очень низких частотах, когда ω << ω0, движение тела массой m, прикрепленного к правому концу пружины, повторяет движение левого конца пружины. При этом x (t) = y (t), и пружина остается практически недеформированной. Внешняя сила 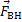 приложенная к левому концу пружины, работы не совершает, т. к. модуль этой силы при ω << ω0 стремится к нулю.
приложенная к левому концу пружины, работы не совершает, т. к. модуль этой силы при ω << ω0 стремится к нулю.
Если частота ω внешней силы приближается к собственной частоте ω0, возникает резкое возрастание амплитуды вынужденных колебаний. Это явление называется резонансом. Зависимость амплитуды xm вынужденных колебаний от частоты ω вынуждающей силы называется резонансной характеристикой или резонансной кривой(рис. 2.5.2).
При резонансе амплитуда xm колебания груза может во много раз превосходить амплитуду ym колебаний свободного (левого) конца пружины, вызванного внешним воздействием. В отсутствие трения амплитуда вынужденных колебаний при резонансе должна неограниченно возрастать. В реальных условиях амплитуда установившихся вынужденных колебаний определяется условием: работа внешней силы в течение периода колебаний должна равняться потерям механической энергии за то же время из-за трения. Чем меньше трение (т. е. чем выше добротность Q колебательной системы), тем больше амплитуда вынужденных колебаний при резонансе.
|
|
|
 2015-02-18
2015-02-18 13410
13410
