Математика

Кеплер нашёл способ определения объёмов разнообразных тел вращения, который описал в книге «Новая стереометрия винных бочек» (1615). Предложенный им метод содержал первые элементы интегрального исчисления\Кроме того, Кеплер очень подробно проанализировал симметрию снежинок. Исследования по симметрии привели его к предположениям о плотной упаковке шаров, согласно которым наибольшая плотность упаковки достигается при пирамидальном упорядочивании шаров друг над другом В ходе астрономических исследований Кеплер внёс вклад в теорию конических сечений. Он составил одну из первых таблиц логарифмов.

У Кеплера впервые встречается термин «среднее арифметическое».

Кеплер вошёл и в историю проективной геометрии: он впервые ввёл важнейшее понятие бесконечно удалённой точки. Он же ввёл понятие фокуса конического сечения и рассмотрел проективные преобразования конических сечений, в том числе меняющие их тип — например, переводящие эллипс в гиперболу.

Механика и физика

Именно Кеплер ввёл в физику термин инерция как прирождённое свойство тел сопротивляться приложенной внешней силе. Заодно он, как и Галилей, формулирует в ясном виде первый закон механики: всякое тело, на которое не действуют иные тела, находится в покое или совершает равномерное прямолинейное движение.

Кеплер вплотную подошёл к открытию закона тяготения, хотя и не пытался выразить его математически. Он писал в книге «Новая астрономия», что в природе существует «взаимное телесное стремление сходных (родственных) тел к единству или соединению». Источником этой силы, по его мнению, является магнетизм в сочетании с вращением Солнца и планет вокруг своей оси

Гравитацию я определяю как силу, подобную магнетизму — взаимному притяжению. Сила притяжения тем больше, чем оба тела ближе одно к другому.

Правда, Кеплер ошибочно полагал, что эта сила распространяется только в плоскости эклиптики. Видимо, он считал, что сила притяжения обратно пропорциональна расстоянию (а не квадрату расстояния); впрочем, его формулировки недостаточно ясны.

Кеплер первый, почти на сто лет раньше Ньютона, выдвинул гипотезу о том, что причиной приливов является воздействие Луны на верхние слои океанов.

Оптика

В 1604 году Кеплер издал содержательный трактат по оптике «Дополнения к Вителлию», а в 1611 году — ещё одну книгу, «Диоптрика». С этих трудов начинается история оптики как науки. В этих сочинениях Кеплер подробно излагает как геометрическую, так и физиологическую оптику. Он описывает преломление света, рефракцию и понятие оптического изображения, общую теорию линз и их систем. Вводит термины «оптическая ось» и «мениск», впервые формулирует закон падения освещённости обратно пропорционально квадрату расстояния до источника света. Впервые описывает явление полного внутреннего отражения света при переходе в менее плотную среду.

Описанный им физиологический механизм зрения, с современных позиций, принципиально верен. Кеплер выяснил роль хрусталика, верно описал причины близорукости и дальнозоркости.

Глубокое проникновение в законы оптики привело Кеплера к схеме телескопической подзорной трубы (телескоп Кеплера), изготовленной в 1613 году Кристофом Шайнером. К 1640-м годам такие трубы вытеснили в астрономии менее совершенный телескоп Галилея.

вопрос 11. Фазовые равновесия. Уравнение состояния многофазной многокомпонентной системы и условия термодинамического равновесия фаз в многокомпонентной системе. Правило фаз Гиббса.

Фазой называется гомогенная часть гетерогенной системы, имеющая во всех точках одинаковые значения интенсивных параметров, которые изменяются скачком на границе раздела фаз.

Фазовым переходом называется переход вещества из одной фазы в другую.

Фазовыми равновесиями называют равновесия в гетерогенных системах, в которых имеют место только фазовые переходы и отсутствуют химические взаимодействия между компонентами.

При переходе из одной фазы (1) в другую фазу (2) dni молей i–ого компонента (например, при конденсации пара или кристаллизации осадка), энергия Гиббса каждой из фаз изменится на величину:

для фазы 1 ,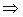

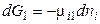для фазы 2 .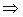

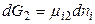Общее изменение энергии Гиббса равно:

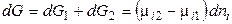. (1)

Если переход происходит в условиях равновесия при T, р = const, то

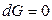, и .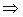

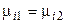Этот вывод распространяется на любой компонент и на любую фазу системы. Итак, равновесию гетерогенных систем отвечает равенство химических потенциалов каждого компонента во всех фазах при T, p = const. Если же химический потенциал некоторого вещества в одной фазе (в одном растворе) будет больше, чем в другой фазе (в другом растворе), то вещество будет самопроизвольно переходитьиз первой фазы в другую.

Рассмотрим систему, содержащую К компонентов и состоящую из Ф фаз, находящихся в равновесии между собой. Состав каждой из фаз определяется концентрациями (К – 1) компонентов, а так как число всех фаз равно Ф, то состав всей системы определится Ф(К– 1) концентрациями всех компонентов. Для полного описания состояния системы необходимы ещё температура и давление, т. е. всего Ф (К – 1) + 2 переменных.

Условием равновесия гетерогенной системы из Ф фаз и К компонентов (как отмечалось ранее) является постоянство температуры и давления, а также равенство всех химических потенциалов каждого из компонентов во всех фазах:

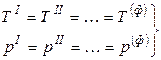, (2)

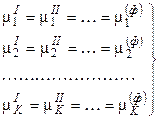. (3)

Здесь верхние индексы обозначают номера фаз, нижние индексы относятся к соответствующим компонентам.

В вышеприведенных равенствах каждое значение m является функцией температуры, давления и концентрации всех компонентов. Например, для двухкомпонентной системы:

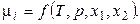
Следовательно, каждое равенство из (4.3) (например 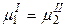) даёт уравнение, связывающее переменные системы. Эти уравнения уменьшают число независимых переменных, характеризующих систему, и называются уравнениями связей.

Обозначим через f число действительно независимых переменных. Тогда

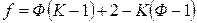, (4)

откуда

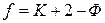. (5)

Последнее соотношение было получено Дж. Гиббсом и носит название уравнения (правила фаз) Гиббса. Равновесные гетерогенные системы, состоящие из любого числа фаз и любого числа веществ, подчиняются правилу фаз Гиббса. Его можно сформулировать следующим образом:

число степеней свободы равновесной термодинамической системы, на которую из внешних факторов влияют только давление и температура, равно числу компонентов системы плюс два, минус число фаз:

,

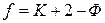где К — число компонентов – веществ, наименьшее число которых необходимо и достаточно для образования всех возможных фаз данной равновесной системы. Компонент является составной частью системы и может быть выделен из нее, и существовать самостоятельно;

f — число степеней свободы – число независимых термодинамических параметров, определяющих состояние системы, изменение которых в определенных пределах не вызывает исчезновения одних и образование других фаз;

число 2 — это число внешних факторов (Р и Т), которые влияют на равновесие.

Перепишем уравнение (4.5) в виде

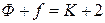, (6)

тогда при 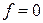находим, что

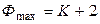, (7)

т.е. максимальное число фаз в гетерогенной системе при равновесии равно числу компонентов плюс два.

Если р или Т = const, то правило фаз Гиббса запишется как

f = К – Ф + 1. (8)

Ги́ббса пра́вило фаз, закон термодинамики многофазных многокомпонентных систем, согласно которому число фаз, сосуществующих в равновесии, не превосходит числа независимых компонентов более чем на 2. Установлено Дж. У. Гиббсом в 1875.

Правило фаз Гиббса определяет соотношение между числом фаз (Ф), компонентов (К), внешних переменных (П) и числом степеней свободы или вариантности (С) термодинамической системы, находящейся в равновесии и записывается следующим образом:

С = К + 2 – Ф;

Цифра 2 в правиле фаз связана с существованием 2-х переменных (температуры и давления), одинаковых для всех фаз. Например, правило фаз Гиббса для постоянного давления запишется как:

С = К +1 – Ф

В этом виде правило фаз применяется для анализа диаграмм фазового равновесия. В случае С = 0 систему принято называть нонвариантной. Она может существовать только при неизменных условиях. Изменение хотя бы одного из параметров системы вызовет изменение числа сосуществующих в системе фаз. При С = 1 система моновариантна. В этом случае только один параметр может быть изменен без одновременного изменения числа фаз; при С = 2 система дивариантна и т. д.

Правило фаз справедливо, если фазы однородны во всем объеме, имеют достаточно большие размеры и отсутствуют полупроницаемые перегородки. Если в системе не происходит химических превращений, то число независимых компонентов равно числу простых веществ, из которых состоит смесь. Если в системе возможны химические взаимодействия, то условия равновесия включают уравнения химических реакций.

Правило фаз Гиббса является основой физико-химического анализа сложных систем, используется для классификации различных случаев химического равновесия.

вопрос 12. Уравнение неразрывности (сплошности) потока.

Рассмотрим зависимость между скоростями в потоке жидкости при условии неразрывности движения.

Для этого выделим внутри потока элементарный параллелепипед, объем которого dV= dxdydz (рис.6). Составляющую скорости вдоль оси х обозначим vх. Тогда через левую грань параллелепипеда площадью dydz в него войдет за бесконечно малый проме­жуток времени масса жидкости, равная

Мх = ρv_xdydzdτ,

где р — плотность жидкости.

Примем допущение, что жидкость несжимаема. Тогда плотность жидкости ρ в потоке постоянна.

Условие неразрывности соблюдается, когда в потоке жидкости не образуются пустоты, не заполненные жидкостью.

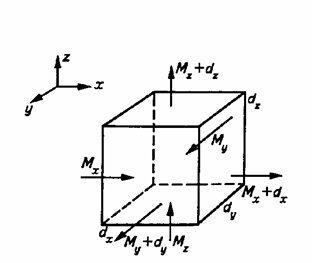
Рис. 4.6. К выводу уравнения неразрывности потока жидкости

Равномерное движение наблюдается, когда скорость, давление, глубина и форма потока не меняются по его длине. Примером равномерного движения является движение жидкости в трубопроводе постоянного сечения с постоянной скоростью.

Неравномерное движение происходит, например, в конической трубе, когда скорость, давление и глубина потока изменяются по длине трубы.

Если рассмотреть поперечное сечение потока жидкости и мысленно представить его состоящим из отдельных элементарных струек, то окажется, что частицы жидкости, которые находятся в струйках, расположенных на различном расстоянии от оси потока, движутся с различными скоростями.

Скорость движения жидкости будет максимальной по оси потока и минимальной в струйках у стенки трубы. Распределение скоростей в потоке зависит от режима движения жидкости.

В технике оперируют не локальными скоростями частиц жидкости, а средней скоростью потока.

Эта скорость представляет собой отношение секундного объемного расхода Vceк к площади поперечного сечения потока F:

v = Vceк / F, (4.1.)

откуда Vceк =vF, а массовый расход, кг/с,

G = ρvF,

где ρ — плотность жидкости, кг/м³.

При движении жидкости через поперечное сечение, отличное от круглого, в качестве расчетного линейного размера принимают гидравлический радиус или эквивалентный диаметр.

Гидравлический радиус вычисляют как отношение площади свободного сечения трубопровода или канала к смоченному периметру

r = F / П, (4.2)

где F — площадь сечения потока, м².

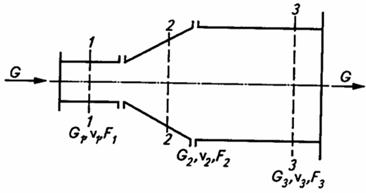
Рис.4.7. К выводу уравнения неразрывности потока для всего объема жидкости

Для цилиндрической трубы

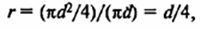
где d – внутренний диаметр трубы.

На противоположной грани параллелепипеда скорость отличается от скорости на левой грани величину 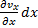и равна

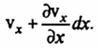
Через правую грань за тот же промежуток времени dτ выйдет масса жидкости

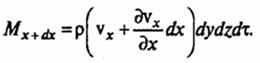
Приращение массы в параллелепипеде

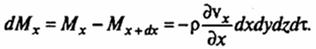
Соответственно вдоль осей y и z изменение массы жидкости

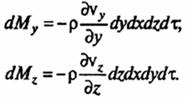
Общее изменение массы жидкости в параллелепипеде за время dτ будет равно сумме ее изменений вдоль осей координат:

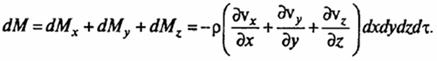
Однако при ρ=const масса жидкости внутри параллелепипеда должна быть постоянной, а следовательно, общее изменение массы dM=0, или

или div v=0, где 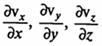- изменение скорости в направлении осей x, y, z.

Это уравнение называется дифференциальным уравнением неразрывности потока несжимаемой жидкости.

Для всего объема потока жидкости из уравнения (4.3) после его интегрирования следует, что при установившемся движении жидкости через каждое поперечное сечение трубопровода проходит в единицу времени одна и та же масса жидкости.

где G – массовый расход, кг/с; .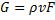

Для несжимаемых капельных жидкостей ρ=const и уравнение (4.4) принимает вид

На основании уравнения (4.5) можно утверждать, что скорости движения капельной жидкости обратно пропорциональны площадям поперечных сечений:

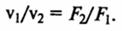
Уравнение (4.4) является частным случаем закона сохранения массы.

вопрос 13. Линейные колебания механических систем. Свободные колебания системы с одной степенью свободы в гармоническом приближении. Частота, амплитуда и фаза колебания. Изохронность колебаний. Вынужденные колебания при отсутствии трения. Резонанс.

Систему называют линейной, если её движение описывается линейными дифференциальными уравнениями.

Колебаниями называется периодический процесс. Гармоническими колебаниями называется периодический процесс с постоянным периодом Т. Число периодов колебаний, происходящих за единицу времени называется частотой колебаний 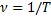. Введем понятие круговой частоты 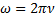. Круговая частота и период связаны, как нетрудно видеть, соотношением 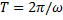. Размерности круговой частоты ω и частоты ν совпадают и равны 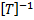обратному времени.

Рассмотрим простую модель осциллятора – модели физического процесса, описываемого уравнениями колебаний. В качестве таковой в дальнейшем исследуется движение точечной массы, привязанной к идеальной пружине. Сила действующая на массу меняется пропорционально удлинению пружины. Такого вида силы вызывают линейные колебания. Строго говоря, модель линейных колебаний справедлива при небольших, в сравнении с характерными размерами физической системы, деформациях. С ростом деформаций относительно положения равновесия в разложении силы могут возникнуть члены пропорциональные квадрату, кубу, … смещения. Такие колебания уже не будут называться линейными. Хотя они, возможно, будут описываться периодическими функциями, но их свойства будут отличны от линейных решений.