Краткая теория. 1. Производственной функцией называется зависимость результата производственной деятельности – выпуска продукции и от обусловивших его факторов – затрат

1. Производственной функцией называется зависимость результата производственной деятельности – выпуска продукции и от обусловивших его факторов – затрат ресурсов х ₁, х ₂,…, х_n. Производственная функция может быть задана как в натуральных, так и в денежных единицах. В последнем случае она представляет собой доход от использования ресурсов.

Производственная функция 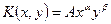называется функцией Кобба-Дугласа. Параметры 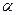и 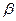представляют собой частные эластичности выпуска продукции по отношению к затратам труда х и капитала y (см. п. 3).

2. Функция полезности U (х ₁, х ₂, …, х_n)задает полезность для потребителя от приобретения х ₁единиц 1-го блага, 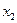единиц 2-го блага и т.д.

3. Частной эластичностью функции нескольких переменных 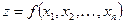относительно переменной х_i, называется величина

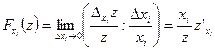(15.19)

Значение 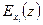показывает приближенно, на сколько процентов изменится переменная z при изменении переменной x_i, на 1 %.

15.107. Производственная функция (в денежном выражении) имеет вид 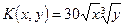(х – количество единиц первого ресурса, у – второго). Стоимость единицы первого ресурса – 5, второго – 10 ден. ед. Найти максимальную прибыль при использовании ресурсов.

Решение. Производственная функция в денежном выражении равна доходу от использования ресурсов. Издержки при этом равны С(х) = 5 х + 10 у. Функция прибыли равна 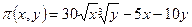. Требуется найти ее максимум.

Частные производные функции 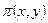равны 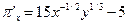; 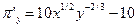. Приравнивая их к нулю, найдем решение х = 81, у = 27. Частные производные второго порядка имеют вид:

, ,

, .

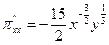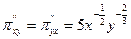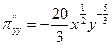
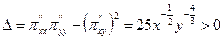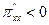Таким образом, найденная критическая точка есть точка максимума. Соответствующее значение прибыли равно 135 (ден. ед.).

15.108. Производственная функция равна 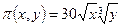, стоимость единицы первого ресурса равна 5, второго – 10. В силу бюджетных ограничений на ресурсы может быть потрачено не более 600ден. ед. В этих условиях найти оптимальное для производителя значение (х, у)количества используемых ресурсов.

Решение. Теперь следует максимизировать функцию 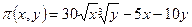, но при условии, что 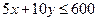. В предыдущей задаче было найдено оптимальное распределение ресурсов в ситуации, когда ограничения отсутствовали. Оказалось, что оптимальные затраты на ресурсы равны 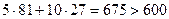. Можно показать, что в этом случае в условиях наличия ограничений на ресурсы следует потратить всю возможную сумму.

Итак, имеем задачу максимизации функции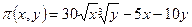

при условии, что 5 х + 10 у = 600, или х + 2 у = 120.

Первый способ. В силу ограничений имеем х = 120 – 2 у и

.

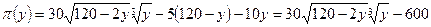Производная функции 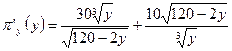. Приравнивая ее к нулю, получим решение у = 24, откуда 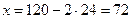. Максимальная прибыль при этом равна 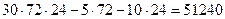(ден. ед.).

Второй способ. При условии, что 5 х + 10 у = 600, функция прибыли имеет вид 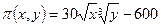. Очевидно, что если какое-то значение С уровня функции 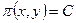должна пересекаться с прямой 5 x + 10 y = 600.

Уравнение линии уровня функции прибыли 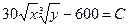может быть записано как 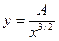, где .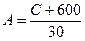

Легко видеть, что максимальное значение А,а следовательно, и уровня С достигается в том случае, если соответствующая линия уровня касается прямой 5 х + 10 у = 600. Так как градиент в каждой точке ортогонален линии уровня, то из этого следует, что условие максимальности прибыли может быть сформулировано следующим образом: вектор 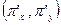ортогонален прямой 5 х + 10 у = 600. Эта прямая имеет угловой коэффициент, равный 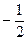. Угловой коэффициент прямой, проходящей через вектор 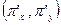равен 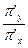. По условию перпендикулярности прямых имеем ,

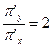т.е. 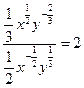или . Подставляя полученное выражение в уравнение

прямой 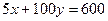, находим х = 72, у = 24.

Замечание. Оптимальное решение лежит на прямой ограничений (в данном случае на прямой 5 х + 10у = 600) только в том случае, если при оптимальном решении без ограничений сумма, затрачиваемая на ресурсы, больше ограничительной. В противном случае решение задачи с ограничениями просто совпадает с решением задачи без ограничений.

15.109. Функция полезности имеет вид: 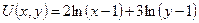. Цена единицы первого блага равна 8, второго – 16. На приобретение этих благ может быть затрачена сумма, равная 1000. Как следует распределить эту сумму между двумя благами, чтобы полезность от их приобретения была бы наибольшей?

Решение. Рассмотрим линии уровня функции полезности 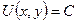, т.е. 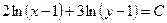. Используя свойства логарифмов, имеем: 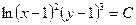, т.е. 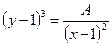, где .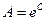

Таким образом, линии уровня представляют собой графики функции

.

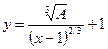Используя рассуждения, приведенные в предыдущем примере, получаем, что в точке (х, у), в которой достигается максимальная полезность, линия уровня касается прямой 8 x + 16 у = 1000, или х + 2 у = 125. Значит, градиент функции полезности должен быть перпендикулярен этой линии. Градиент функции полезности имеетвид 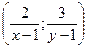. Угловой коэффициент прямой 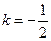. Используяусловие перпендикулярности прямых, имеем: 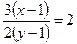или .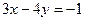

Следовательно, оптимальное распределение потребления товаров находится как решение системы:

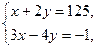т.е. x = 49,5; y = 37,75.