Краткая теория. 1. Рассмотрим множество D на плоскости

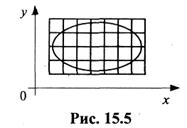
1. Рассмотрим множество D на плоскости. Построим покрывающую это множество решетку (рис. 15.5).

Пусть 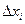и 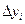– соответственно длина горизонтальной и вертикальной клетки 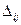. Выберем в каждой клетке 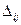точку .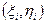

Интегральной суммой функции 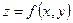на множестве D называется сумма

.

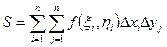2. Функция 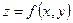называется, интегрируемой на множестве D, если существует конечный предел I интегральной суммы этой функции на D при условии 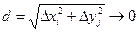. Само значение предела I называется двойным интегралом функции 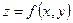на множестве D:

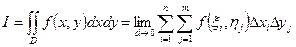. (15.17)

3. Если область D имеет вид, изображенный на рис. 15.6,

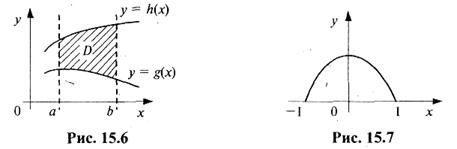
то имеет место равенство

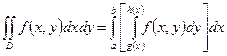. (15.18)

15.100. Вычислить 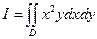, где D – полукруг, изображенный на рис. 15.7.

Решение. Имеем 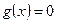, 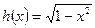– функции, задающие нижнюю и верхнюю границы области.

По формуле (15.18):

.

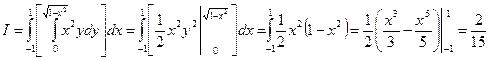15.101. Вычислить 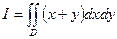, где D – область, ограниченная параболами 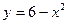, , 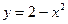прямой 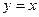и осью ординат.

Решение. Область D изображена на рис. 15.8.

Разобьем область D на две области прямой, проходящей через точку М параллельно оси ординат. Точка М имеет абсциссу, равную 1, точка N – равную 2. Таким образом, имеем:

.

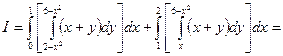
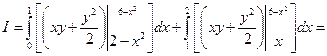
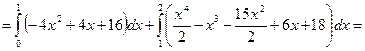
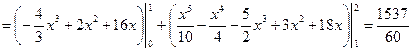Вычислить двойные интегралы:

15.102. 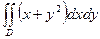, где D ограничена прямыми у = х, у = 2х и у = -х + 4.

15.103. 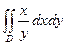, где D ограничена прямыми 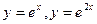и прямой х = 2.

15.104. 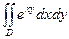, где D ограничена гиперболой ху = 1, осью абсцисс и прямыми х = 2, х = 3.

15.6. Функции нескольких переменных в экономических задачах