Одной из основных задач дифференциального исчисления является нахождение производной функции или дифференциала заданной функции.
Первой основной задачей интегрального исчисления является обратная задача – отыскание функции по ее производной или заданному ее дифференциалу. Второй основной задачей интегрального исчисления является определение площади плоской области и объема тела вращения.
Функция 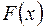 называется первообразной для функции
называется первообразной для функции 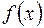 , если функции
, если функции 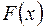 и
и 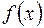 связаны следующим соотношением:
связаны следующим соотношением:
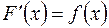 .
.
Пример. Функция 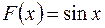 вяляется первообразной для функции
вяляется первообразной для функции 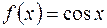 , так как
, так как 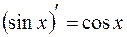 .
.
Если для данной функции 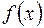 существует первообразная, то она не является единственной. Так, в предыдущем примере в качестве первообразных можно взять следующие функции:
существует первообразная, то она не является единственной. Так, в предыдущем примере в качестве первообразных можно взять следующие функции:
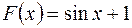 ,
, 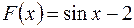
или в общем виде
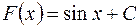 ,
,
где 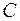 – произвольная постоянная, так как при любом значении
– произвольная постоянная, так как при любом значении 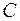
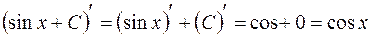 .
.
В связи с этим возникает вопрос, исчерпывает ли функция вида 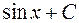 все возможные первообразные для
все возможные первообразные для 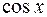 или существуют еще функции другого вида, которые также будут первообразными для
или существуют еще функции другого вида, которые также будут первообразными для 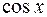 .
.
|
|
|
Ответ на него дает следующая теорема.
Теорема. Если 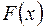 есть какая-либо из первообразных для данной функции
есть какая-либо из первообразных для данной функции 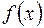 , то самое общее выражение для первообразной имеет вид:
, то самое общее выражение для первообразной имеет вид:
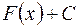 ,
,
где 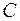 – есть первообразная постоянная.
– есть первообразная постоянная.
Доказательство. Пусть 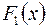 есть любая функция, имеющая своей производной
есть любая функция, имеющая своей производной 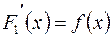 .
.
С другой стороны, рассматриваемая функция 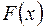 также имеет
также имеет 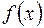 своей производной, то есть
своей производной, то есть 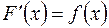 .
.
Вычитая это равенство из предыдущего, имеем:
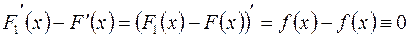
и, следовательно,
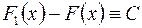 ,
,
где 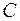 есть постоянная, что и требовалось доказать.
есть постоянная, что и требовалось доказать.
Действительно, если производная некоторой дифференцируемой функции 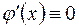 , то сама функция
, то сама функция 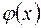 может быть только постоянной.
может быть только постоянной.
Полученный результат можно сформулировать и так: если производная (или дифференциалы) двух функций тождественно равны, то сами функции отличаются лишь постоянным слагаемым.
Если функция 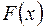 является первообразной для
является первообразной для 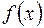 , то семейство всех ее первообразных функций
, то семейство всех ее первообразных функций 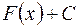 называется неопределенныминтегралом от функции
называется неопределенныминтегралом от функции 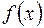 и обозначается как
и обозначается как 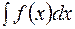 .
.
Таким образом, по определению
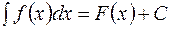 ,
,
если
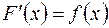 .
.
При этом функцию 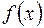 называют подынтегральной функцией,
называют подынтегральной функцией, 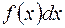 – подынтегральным выражением, переменную
– подынтегральным выражением, переменную 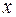 – переменной интегрирования, а знак
– переменной интегрирования, а знак 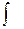 – знаком интеграла. Действие, с помощью которого по данной функции
– знаком интеграла. Действие, с помощью которого по данной функции 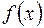 находим ее первообразную
находим ее первообразную 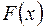 , называется интегрированием функции
, называется интегрированием функции 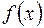 .
.
Пример. Найти неопределенный интеграл от функции 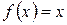 .
.
Решение. Первообразной от 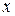 будет функция
будет функция 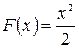 , так как
, так как 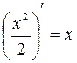 . В таком случае
. В таком случае 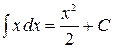 , где
, где 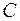 – произвольная постоянная.
– произвольная постоянная.
Таблица основных интегралов
Степенные функции:
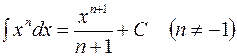 ;
;
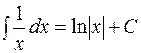 .
.
Показательные функции:
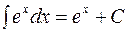 ;
;
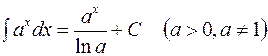 .
.
Тригонометрические функции:
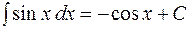 ;
;
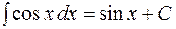 ;
;
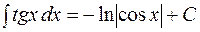 ;
;
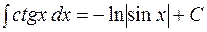 ;
;
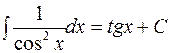 ;
;
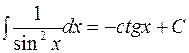 .
.
Дробные рациональные функции:
|
|
|
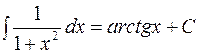 ;
;
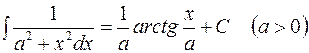 ;
;
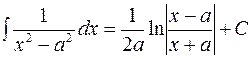 .
.
Иррациональные функции:
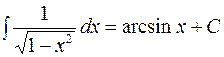 ;
;
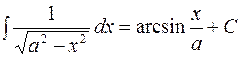 ;
;
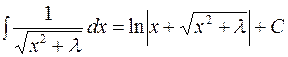 .
.
 2015-03-22
2015-03-22 777
777








