Применение сочетаний. Сочетание можно интерпретировать как размещение неразличимых предметов

Пример 1. Найдем вероятность угадать 7 номеров из 49 (игра спортло-то). Количество вариантов равно числу сочетаний из 49 элементов по 7. Су-ществует единственный благоприятный вариант. Отсюда вероятность равна .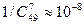

Теорема 4. Число возрастающих функций {1,2, ×××,k} ® {1,2, ×××,n } равно .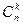

Теорема 5. Число последовательностей натуральных чисел (x₁, x₂, ×××, x_k), x_i³1, удовлетворяющих уравнению

x₁ + x₂ + ××× + x_k = n,

равно .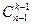

Теорема 6. Число неубывающих сюръекций {0,1, ×××, n –1} ® {0, 1, ×××, k–1 } равно .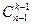

Доказательство. Каждая сюръекция задает разбиение множества { 0, 1, ×××, k–1 } на подмножества f ^─1(0), f ^─1(1), ×××, f ^─1(n –1). Пусть m₀ – наибольший в f ^─1(0), m₁ – наибольший в f ^─1(1), ×××, m_n-2 – наибольший в f^─1(n –2). Тогда m_n-1 = k – 1. Следовательно,

0 ≤ m₀ < m₁ < ××× < m_n-2 ≤ k-2.

Число таких последовательностей равно 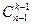– количеству возрастающих функций n–1 ® k–1.

Пример 2. Число неубывающих сюръекций n ® 1 равно .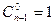

Число неубывающих сюръекций 3 ® 2 равно .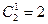

Сочетания с повторениями. Сочетанием с повторением из множества { e₁ , e₂ , ×××, e_n } называется линейная комбинация x₁e₁ + x₂e₂ + ××× +x_n e_n, состоящая из x₁ элементов e₁ , из x₂ элементов e₂ ,×××, из x_n элементов e_n, где x_i ≥ 0 – неотрицательные целые числа. Если x₁ + ××× +x_n = k, то оно называется сочетанием с повторениями из n по k.

Пусть, например, имеется 3 цвета: красный, зеленый, синий. Интенсивности этих цветов равны. Сколько смесей суммарной интенсивности 10 можно получить, смешивая x₁ красных, x₂ зеленых и x₃ синих цвета?

Лемма 1. Пусть 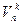- число сочетаний с повторениями из n по k. Тогда 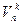равно числу неубывающих функций {1,2, ×××, n-1} ® {0,1,2, ×××, n}