Решение. Начнем с построения сетевого графа

Начнем с построения сетевого графа.

2 5

12 11

1098 7

3 139

1 7

8 13 9

12 9

4 8

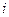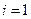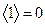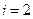Найдем ранее начало операций для всех этапов . Для по определению . Для получаем 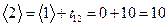. Аналогично, при 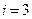раннее начало определяется соотношением 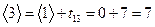; а при 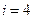- соотношением 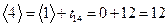. Первое отличие в рассуждениях возникает при 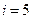. В эту вершину сетевого графа идет три стрелки – из вершин 2, 3 и 4. Следовательно, мы должны рассмотреть три выражения

, , ,

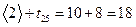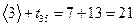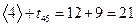и взять наибольшее из них, то есть 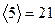. Далее, в вершину 6 ведет две операции, из вершины 2 и из вершины 5. Следовательно,

.

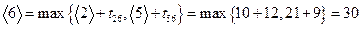Для вершины 7 все просто: 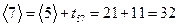. В вершину 8 ведет две операции, из вершины 4 и из вершины 5,

.

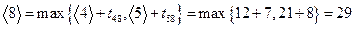И, наконец, в вершину 9 идет три стрелки – из вершин 6, 7, 8. Следовательно,

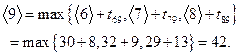
Таким образом, минимальное время выполнения всех операций технологического цикла равно 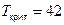дня.

Определим теперь позднее время окончания операций для каждого этапа 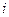. По определению, 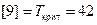. Из вершин 6, 7, 8 начинается ровно по одной операции, поэтому

,

,

.

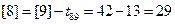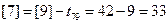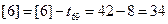Из вершины 5 выходит три стрелки, в вершину 8, 7 и в вершину 6 соответственно, следовательно,

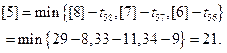
В вершине 4 начинается две операции, 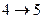, 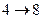. Таким образом,

.

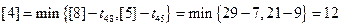Для 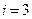получаем 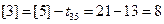. Для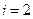

.

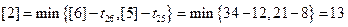Остается рассмотреть случай :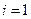

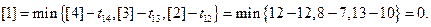Критическими вершинами оказались этапы 1, 4, 5, 8, 9. Единственный критический путь в нашем графе – это путь

.

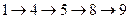Определим резервы, полный и свободный, всех операций.

, ,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

.

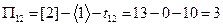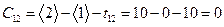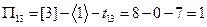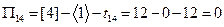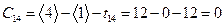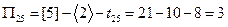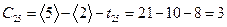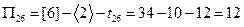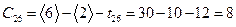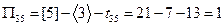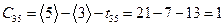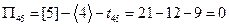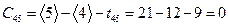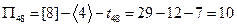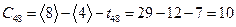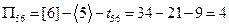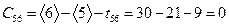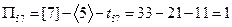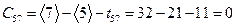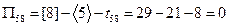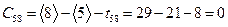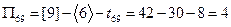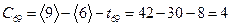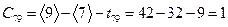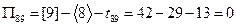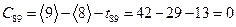Запишем полученные результаты в виде таблицы.

Операция	Продолжительность	Полный резерв	Свободный резерв	Раннее начало	Раннее окончание	Позднее начало	Позднее окончание

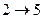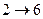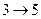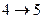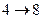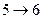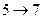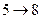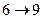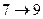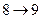Теперь перейдем к построению календарных графиков. Будем сначала исходить из ранних сроков выполнения всех операций. Будем изображать количество рабочих 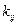, занятых на выполнении операции 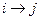в промежутке с 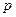–того по 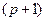–тый день в виде прямоугольника с основанием 1 и высотой .

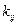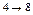
13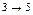

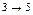
11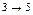

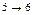
10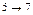

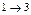
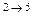
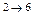
7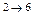

6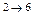

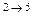
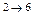
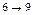
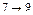
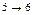
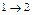
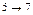
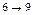
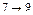
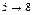
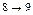
7 10 12 18 20 21 22 29 32 42

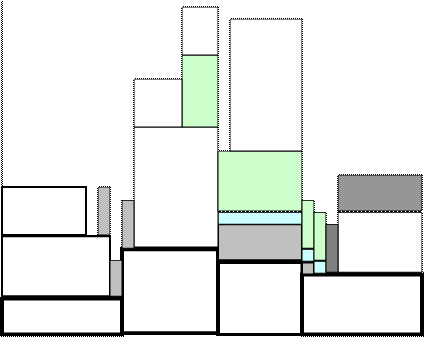
Начнем с критических операций. Отвечающие критическим операциям прямоугольники будем изображать жирными линиями на диаграмме. Эту часть диаграммы нельзя сдвинуть по времени. Точно также мы не будем сдвигать по времени операции, имеющие нулевой свободный резерв. Это операции 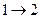, , 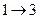, 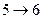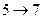. Начала всех остальных операций сдвинем на величину их свободного резерва.

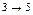
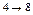
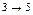
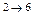
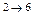
10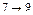

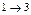
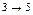
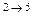
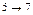
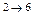
7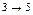

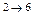
6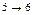

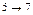
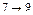
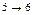
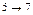
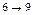
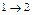
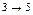
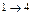
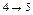
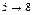
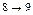
7 10 12 21 22 29 32 42

Как видно из диаграмм, при первом способе планирования максимальная потребность в рабочей силе равна 22 человекам, и при втором – 21 человеку.

Перейдем ко второй части курса, в котором мы разберем метод динамического программирования на примере решения задачи об оптимальном распределении ресурсов.

Сформулируем требования к моделям, которые могут быть решены методом динамического программирования и выпишем основное уравнение динамического программирования, называемое уравнением Беллмана.

В дискретных моделях динамического программирования мы имеем дело с управляемой системой, которую мы можем переводить из одного состояния в другое за счет выбора управления из некоторого множества управлений. Процедуру перевода системы из одного состояния в другое повторяют 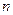раз. Для каждого шага 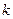известен список возможных состояний системы

, , …, ,

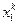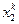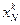и список состояний 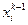, в которые систему можно перевести из состояния :

.

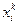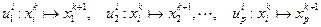Выбирать, в какое состояние можно перевести систему из данного состояния, можно произвольным образом. Результатом каждого такого выбора является цепочка

,

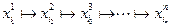называемая допустимым процессом. Графически эту последовательность переходов можно изобразить в виде графа, вершины которого изображают возможные состояния системы, а стрелки – возможные переходы из одного состояния в другое.

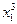
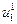
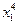
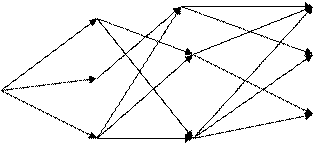
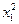
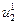
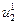
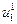
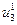
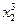
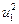
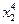
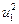
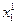
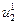
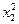
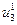
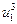
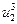
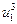
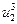
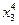
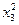
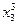
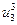
В это примере всего имеется 4 этапа. На первом этапе состояние системы единственное – это 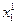. На втором, третьем и четвертом этапах имеется по три возможных состояний системы. На первом этапе допустимы переходы 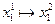, , 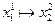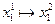. На втором этапе возможны следующие переходы:

из состояния 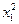возможны переходы , ;

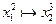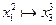из состояния 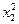возможен переход ;

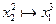из состояния 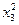возможны переходы , .

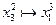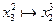На третьем этапе возможны следующие переходы.

Из состояния : , ;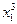

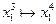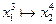из состояния : , ;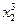

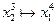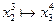из состояния : , , .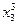

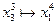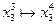На каждом шаге качество принятого решения оценивается некоторой функцией 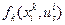, зависящей от состояния 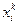и используемого управления 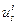(проще всего считать, что 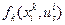- это прибыль). Функционал, описывающей качество принятых решений на всех этапах, есть сумма

.

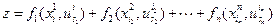В этих условиях требуется определить цепочку допустимых переходов системы из одного состояния в другое, обеспечивающую максимальное значение функции .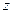

Основная идея динамического программирования заключается в следующем. Вместо того чтобы выписывать все возможные цепочки переходов системы из одного состояния в другое и для каждой из таких цепочек определять значение функции 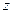, поступают следующим образом. Сначала рассматривают все возможные состояния 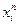системы на последнем этапе (независимо от того, можно ли вообще прийти в это состояние из заданного начального положения системы, и, если можно, то, с помощью какого именно процесса), и для каждого такого состояния определяют максимум функции 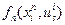. Обозначим 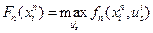. Для 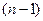–го шага вновь рассмотрим все возможные состояния 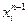и положим

.

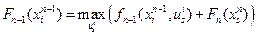Разъясним смысл выписанной формулы. Зафиксируем 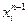и выберем какое-либо управление 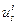. Оно переведет систему из состояния 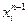на 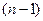–ом шаге в состояние 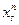на 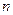–м шаге. Прибыль от принятого решения складывается из прибыли этапа 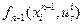и максимально возможной прибыли всех следующих этапов 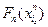(в нашем случае пока только одного, последнего этапа). Таким образом, суммарная прибыль равна 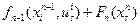. Естественно, если мы попали в состояние 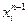на 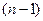–м шаге, то мы должны управлять системой так, чтобы обеспечить максимум функции 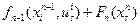. Таким образом, смысл функции 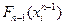– максимальная прибыль, которую можно получить на двух последних этапах, если на 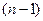–м шаге мы перевели систему в состояние .

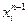Теперь мы можем написать общее уравнение Беллмана для нашей задачи. Обозначим через 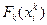- максимум суммы 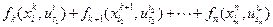по всем допустимым управлениям для системы, находящейся на 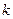–м шаге в состоянии 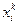. Тогда

.

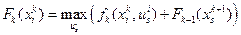При этом 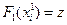. Выписанное уравнение называется уравнением Беллмана. Функции 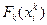определяются последовательно, начиная с конца 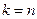. Метод динамического программирования для решения задач оптимального управления описанного вида состоит, следовательно, в последовательном определении функций 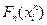, , 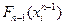…, , 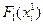и тех управлений 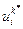, которые обеспечивают максимум функции 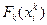в соотношении 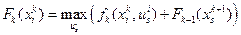. Решим с помощью метода динамического программирования следующую задачу об оптимальном распределении капиталовложений между предприятиями.

Задача 7.2. Фирма, в состав которой входит три предприятия, принимает решение о комплексной реконструкции этих предприятий. В следующей таблице указаны 4 возможных решения по каждому предприятию, затраты c_i на реализацию таких решений и чистая прибыль R_i как результат принятого решения (в млн. руб.)

	1-е предприятие	2-е предприятие	3-е предприятие
с1	R1	c2	R2	c3	R3
Оставляем в прежнем виде
Малая механизация
Частичная модернизация
Полная реконструкция

Требуется, используя метод динамического программирования, составить план реконструкции предприятий, обеспечивающий максимальную прибыль, при условии, что фирма может вложить в реконструкцию предприятий не более 39 млн. руб.