Используя выражение комплексного коэффициента передачи напряжения в области высоких частот, запишем оператор цепи:
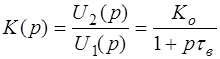 ,
,
где 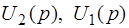 - изображения по Лапласу выходного и входного сигналов. Для функции
- изображения по Лапласу выходного и входного сигналов. Для функции 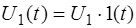 её изображение будет:
её изображение будет: 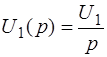 . Следовательно, изображение выходного сигнала:
. Следовательно, изображение выходного сигнала: 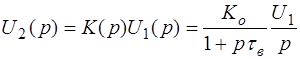
Переходя от изображения по Лапласу 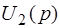 к оригиналу, запишем:
к оригиналу, запишем:
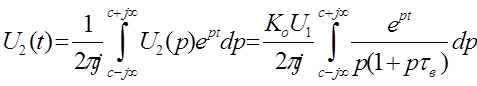 (4.11)
(4.11)
Очевидно, два полюса: p1, p2 подынтегральной функции (4.11) располагаются в начале координат: р1=0 и на отрицательной действительной оси: 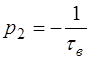 . Поэтому, переходя от линейного интеграла (4.11) к контурному с бесконечно большим радиусом, охватывая им сначала всю левую полуплоскость, а затем к двум контурным интегралам С 1, С 2, охватывающим полюсы р1 и p2, запишем:
. Поэтому, переходя от линейного интеграла (4.11) к контурному с бесконечно большим радиусом, охватывая им сначала всю левую полуплоскость, а затем к двум контурным интегралам С 1, С 2, охватывающим полюсы р1 и p2, запишем:
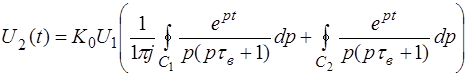
Для вычисления интегралов в последнем выражении воспользуемся формулой Коши:
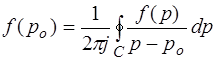
где контур С охватывает полюс ро, а f(p) – аналитическая функция комплексного переменного р. Поэтому контурный интеграл C1 для первого полюса Р1 согласно формуле Коши дает:
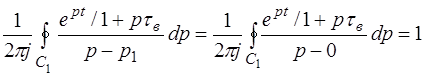
Для вычисления второго контурного интеграла преобразуем его к виду:
|
|
|
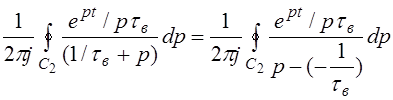
Тогда:
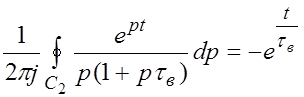 .
.
Следовательно, переходный процесс для области малых времен будет: 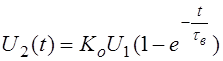 .
.
 2015-03-27
2015-03-27 254
254







