КИНЕМАТИКА ТЕКУЧЕГО ТЕЛА
Л. Эйлер и Ж. Лагранж предложили два метода изучения движения жидкости.
По Лагранжу за движением отдельной частицы жидкости наблюдают, исследуя её траекторию. Координаты x 0, y 0, z 0, соответствующие начальному моменту времени t 0, рассматривают как наименование частицы, позволяющее в любой момент отличить её от других частиц. Положение частицы, определяемое радиус-вектором r или декартовыми координатами x, y, z, есть функция её начальных координат x 0, y 0, z 0 и времени t:
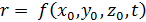 ;
;
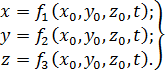 (3.1)
(3.1)
Величины x 0, y 0, z 0, а также скорости и давления, связанные с движущимися элементарными объёмами сплошной среды, называют переменными Лагранжа.
Скорость частицы и проекции скорости на координатные оси определяются дифференцированием (3.1) по времени (при постоянных начальных координатах x 0, y 0, z 0):
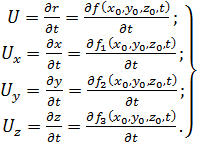 (3.2)
(3.2)
Ускорение частицы и его проекции на координатные оси определяются дифференцированием уравнений (3.2) по времени:
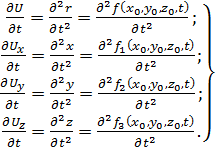 (3.3)
(3.3)
Производную по времени, вычисляемую в переменных Лагранжа, называют субстанциальной (как относящуюся к определенной частице субстанции).
|
|
|
Метод Лагранжа, дающий подробное описание движения каждой частицы, не получил распространения из-за своей громоздкости и сложности.
Для решения практических задач важно знать не столько поведение индивидуальной частицы, сколько состояние движения в каждый момент времени в каждой точке пространства. Такой подход к описанию движения предложил Л. Эйлер.
По Эйлеру исследуется зависимость скорости частиц в определенной точке пространства (через которую частицы непрерывно следуют одна за другой) от координат точки x, y, z и от времени t:
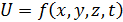 , (A)
, (A)
или, в проекциях на оси координат:
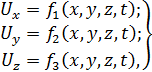 (3.4)
(3.4)
где величины x, y, z называют переменными Эйлера. Эйлеровыми переменными называют и характеристики сплошной среды (поле скоростей, поле давлений, поле напряжений и т. п.), отнесённые к фиксированным элементам геометрического пространства (точкам, линиям, поверхностям, объёмам).
Величины x, y, z имеют в методах Лагранжа и Эйлера различный смысл. По Лагранжу эти величины представляют переменные координаты одной и той же частицы движущейся жидкости. По Эйлеру - это постоянные координаты одних и тех же точек пространства, через которые в разные моменты времени проходят различные частицы жидкости.
Если уравнения (3.4) рассмотреть для некоторого момента времени t, то получим распределение скоростей частиц жидкости в пространстве для этого момента.
При постоянных значениях x, y, z и переменном t получим зависимость скорости жидкости от времени в данной точке пространства, причем в разные моменты времени скорости будут относиться к разным частицам жидкости.
|
|
|
В том случае, когда желательно выяснить, каким образом изменяется с течением времени скорость в точке (x, y, z) пространства, следует продифференцировать уравнения (3.4) по времени, считая координаты x, y, z постоянными.
Если же нас интересует, каким ускорением обладает частица, проходящая в данный момент времени через точку (x, y, z), то следует рассматривать координаты x, y, z как величины, зависящие от времени. Ведь за малый промежуток времени dt, в течение которого мы наблюдаем за изменением скорости частицы, она успевает перейти из точки (x, y, z) в другую точку.
Таким образом, скорость частицы зависит от времени как непосредственно, так и через посредство координат x, y, z, в свою очередь являющихся функциями времени. Поэтому ускорение частицы следует вычислять, дифференцируя (A) как сложную функцию:
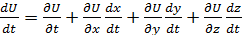 . (3.5)
. (3.5)
Так как
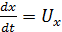 ;
; 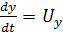 ;
; 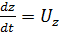 ,
,
то
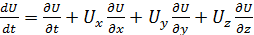 . (3.6)
. (3.6)
Аналогично для компонент ускорения частицы
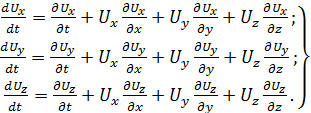 (3.7)
(3.7)
Первый член правой части уравнения (3.6) 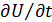 выражает локальное ускорение (местное) частицы. Он характеризует изменение скорости во времени в данной точке пространства, обусловленное нестационарностью поля скоростей. Последующие три члена представляют изменения скорости частицы, обусловленные изменением её координат, и называются конвективными ускорениями.
выражает локальное ускорение (местное) частицы. Он характеризует изменение скорости во времени в данной точке пространства, обусловленное нестационарностью поля скоростей. Последующие три члена представляют изменения скорости частицы, обусловленные изменением её координат, и называются конвективными ускорениями.
Символически вынося вектор 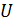 за скобки в уравнении (3.6), получим
за скобки в уравнении (3.6), получим
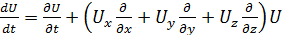 . (3.6a)
. (3.6a)
Выражение в скобках представим как скалярное произведение вектора
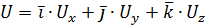 (B)
(B)
на символический вектор 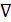 - дифференциальный оператор (Гамильтона) набла
- дифференциальный оператор (Гамильтона) набла
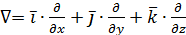 , (C)
, (C)
то есть 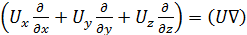 и, следовательно,
и, следовательно,
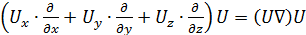 . (D)
. (D)
Аналогично преобразовав уравнения (3.7), перепишем (3.6) и (3.7) в виде
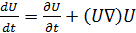 ; (3.8)
; (3.8)
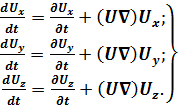 (3.9)
(3.9)
 2015-03-27
2015-03-27 1898
1898







