Определение 8.3 Функция 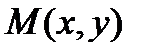 - называется однородной степени
- называется однородной степени 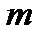 , если
, если 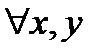 и
и 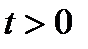 выполняется равенство
выполняется равенство
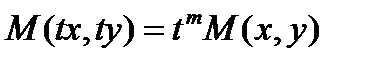 (8.16)
(8.16)
Пример 8.5: Функция 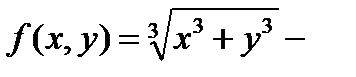 однородная функция первого порядка
однородная функция первого порядка
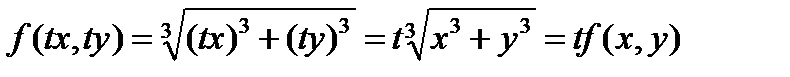
Пример 8.6: Функция 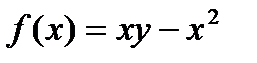 есть однородная функция второго порядка, так как
есть однородная функция второго порядка, так как
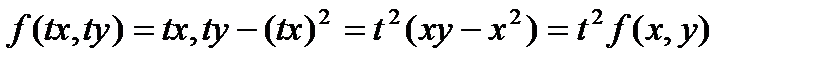
Пример 8.7: Функция 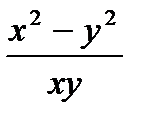 есть однородная функция нулевого измерения. Действительно,
есть однородная функция нулевого измерения. Действительно,
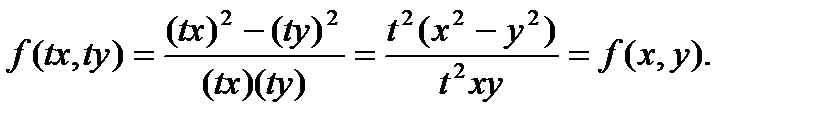
Определение8.4 Если функции 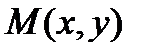 и
и 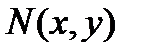 однородные, одной и той же степени m, то дифференциальное уравнение
однородные, одной и той же степени m, то дифференциальное уравнение
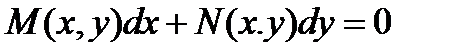 (8.161)
(8.161)
называется однородным.
Определение 8.5. Дифференциальное уравнение первого порядка
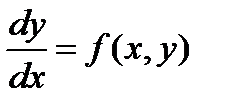 (8.17)
(8.17)
называется однородным относительно 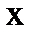 и
и 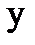 ,если
,если 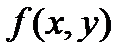 есть однородная функция нулевого измерения.
есть однородная функция нулевого измерения.
Решение уравнения (8.17). Его можно преобразовать, следующим образом
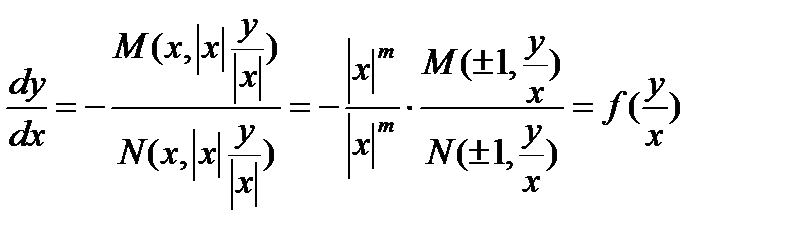
То есть 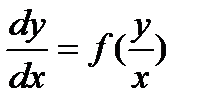 (8.18)
(8.18)
Где 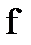 - некоторая функция от одного переменного.
- некоторая функция от одного переменного.
Введем вместо 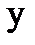 новую функцию
новую функцию 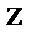 от (
от (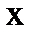 ) при помощи подстановки
) при помощи подстановки
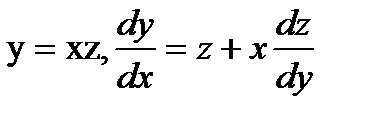 (8.19)
(8.19)
Тогда (8.19), подставляя в (8.18) имеем
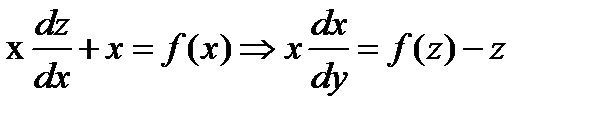
Или
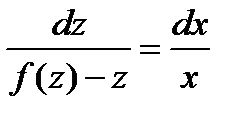
Следовательно, в силу (8.10) получим
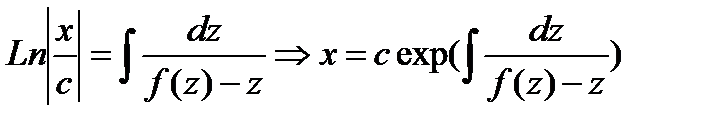 (
(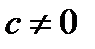 )
)
Таким образом, решение уравнение (8.17) дается формулой
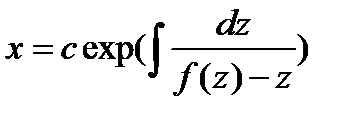 (
(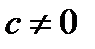 ) (8.20)
) (8.20)
Пример8.8: Решить уравнение 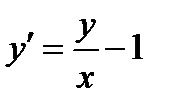
Решение: Заметим, что 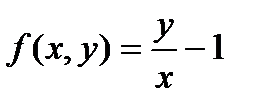 является однородной функцией нулевого измерения
является однородной функцией нулевого измерения
|
|
|
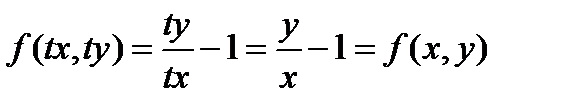
Тогда согласно формуле (8.20), имеем
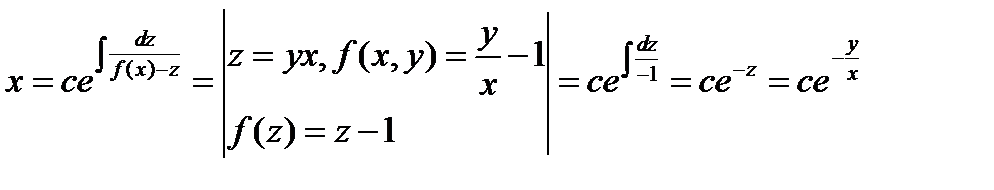
Пример 8.9: Решить уравнение
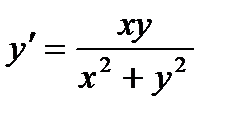 (8.21)
(8.21)
Решение: Так как 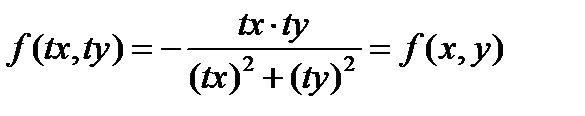 , следовательно(8.21) является однородным уравнением и имеем
, следовательно(8.21) является однородным уравнением и имеем 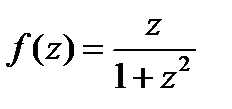 , следовательно, по формуле (8.20) имеем
, следовательно, по формуле (8.20) имеем
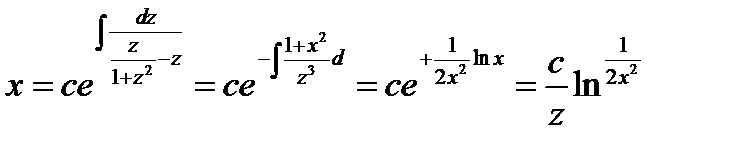
Откуда
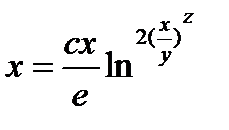 .
.
Замечание8.2: Иногда, уравнение можно привести к однородному заменой переменного
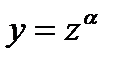 (α-постоянное). Это имеет место в том случае, когда в уравнении все члены оказываются одного измерения, если переменному
(α-постоянное). Это имеет место в том случае, когда в уравнении все члены оказываются одного измерения, если переменному 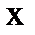 приписать 1, переменному
приписать 1, переменному 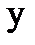 - измерение α и производной.
- измерение α и производной.
Пример8.10: Решить уравнение
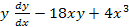 =0
=0
Решение: Пологая y= 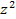 имеем
имеем
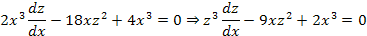
Далее пологая z=Ux, имеем
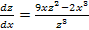
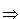 U’
U’ 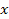 =
= 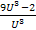 ,
,
Откуда
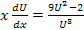 ,
, 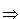
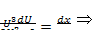
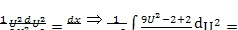
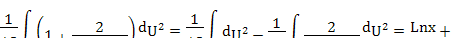
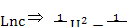 Ln
Ln 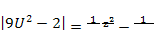 Ln
Ln 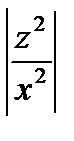 =Ln
=Ln 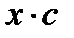
Так как 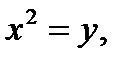 имеем
имеем
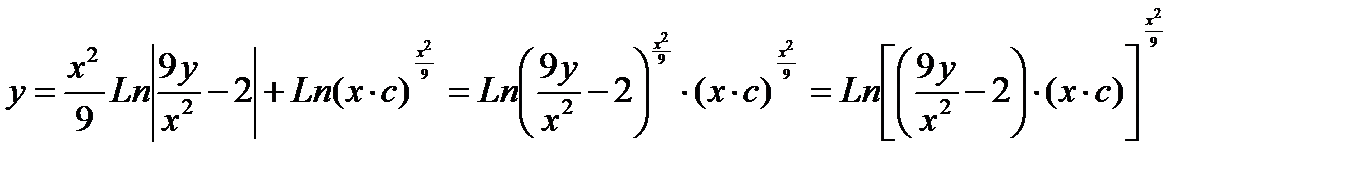
 2015-03-07
2015-03-07 404
404








