Теорема Абеля. Интервал и радиус сходимости

Теорема Абеля. Если степенной ряд (19.2) сходится при х=х_о ≠0, то он сходится, и притом абсолютно, при всяком х, лежащем в интервале 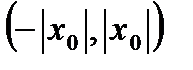, то есть удовлетворяющем условию: < .

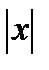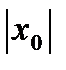Доказательство. Заметим, что вследствие сходимости ряда 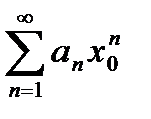его общий член стремится к нулю: а_пхⁿ 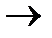0 (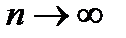); поэтому все члены этого ряда ограниченны, то есть существует такое постоянное число М, что при всяком п имеет место неравенство:

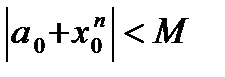
Запишем ряд (19.2) так:

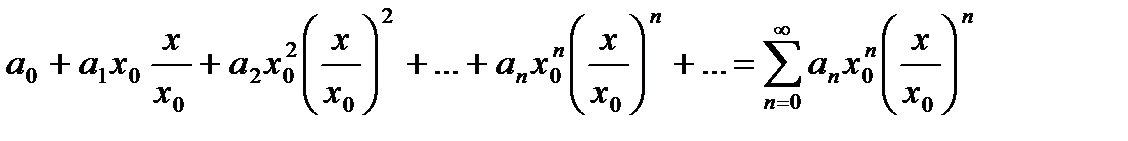
составим ряд из абсолютных величин этого ряда:

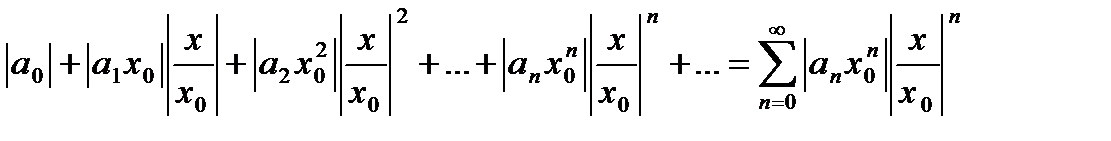
В силу установленного равенства каждый член здесь меньше соответствующего члена геометрической прогрессии со знаменателем

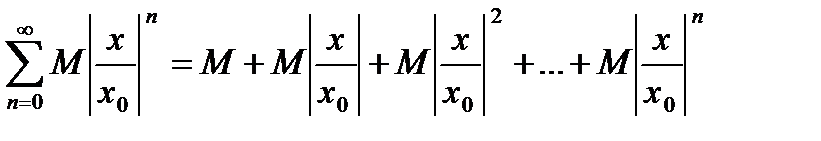
если |х|<|х_о|, то < 1 и прогрессия сходится. Поэтому сходится и ряд по абсолютной величине, а значит, абсолютно сходится и ряд (19.2).

Теорема доказана.

Несмотря на то, что 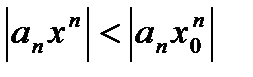, то мы не можем сразу воспользоваться признаком сравнения, поскольку в условии теоремы не сказано, что ряд в самой точке х₀ сходится абсолютно.

Следствие 19.1 Если степенной ряд (19.2) расходится при х=х₀, то он расходится и при всяком х, большем по абсолютной величине, чем х₀, то есть при |х|>|х_о|.