1. Интегралы вида
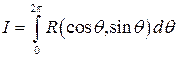 , (1)
, (1)
где 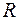 – рациональная функция своих аргументов, приводятся к интегралу по замкнутому контуру от функции комплексной переменной.
– рациональная функция своих аргументов, приводятся к интегралу по замкнутому контуру от функции комплексной переменной.
Произведем замену 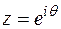 , тогда
, тогда 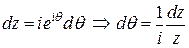 . Выразим косинус и синус через переменную
. Выразим косинус и синус через переменную 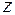 :
:
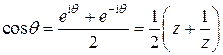 ;
; 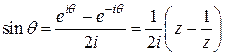 .
.
При изменении угла  от
от  до
до 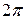 переменная
переменная 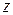 пробегает единичную окружность в положительном направлении. Значит, интеграл (1) принимает вид
пробегает единичную окружность в положительном направлении. Значит, интеграл (1) принимает вид
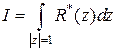 ,
,
где обозначено 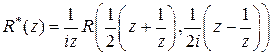 . В силу основной теоремы о вычетах этот интеграл равен
. В силу основной теоремы о вычетах этот интеграл равен
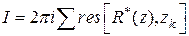 , (2)
, (2)
где 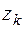 – особые точки рациональной функции
– особые точки рациональной функции 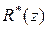 , лежащие в круге
, лежащие в круге 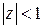 .
.
Пример 1. Вычислить интеграл 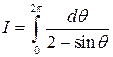 .
.
Решение. Напомним, что такой интеграл раньше мы вычисляли с помощью универсальной тригонометрической подстановки 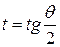 . Покажем, как воспользоваться формулой (2).
. Покажем, как воспользоваться формулой (2).
Полагая 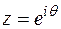 , с учетом приведенных выше формул найдем
, с учетом приведенных выше формул найдем
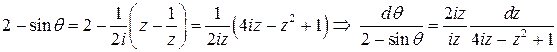 .
.
В результате заданный интеграл преобразуется к виду 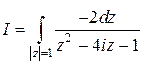 . Подынтегральная функция имеет простые полюсы в точках
. Подынтегральная функция имеет простые полюсы в точках 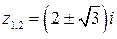 (это нули знаменателя). Только одна из этих точек, а именно
(это нули знаменателя). Только одна из этих точек, а именно 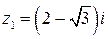 лежит в круге
лежит в круге 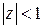 . Найдем (формула (6) предыдущего пункта)
. Найдем (формула (6) предыдущего пункта)
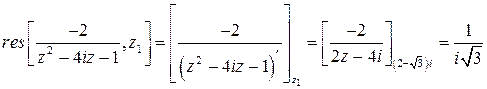 .
.
Поэтому в силу формулы (2)
|
|
|
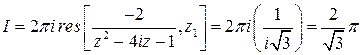 . ☻
. ☻
Задача 1. Убедиться, что
1) 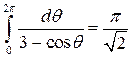 ; 2)
; 2) 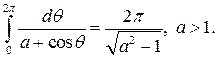
2. Интегралы вида
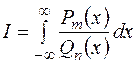 . (3)
. (3)
Здесь 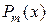 и
и 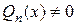 – многочлены степени соответственно
– многочлены степени соответственно 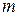 и
и 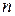 ,
, 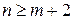 .
.
Вычисление таких интегралов проводится по следующей схеме.
1) Вводим функцию комплексной переменной 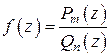 , аналитическую на действительной оси в силу условия
, аналитическую на действительной оси в силу условия 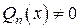 (то есть строим аналитическое продолжение подынтегральной функции
(то есть строим аналитическое продолжение подынтегральной функции 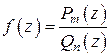 на комплексную плоскость).
на комплексную плоскость).
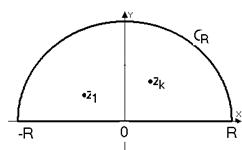 2) Принимаем в качестве контура интегрирования
2) Принимаем в качестве контура интегрирования  границу полукруга
границу полукруга 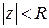 ,
, 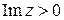 :
: 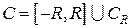 . При этом радиус
. При этом радиус 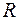 полуокружности
полуокружности 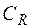 считается столь большим, что все особые точки
считается столь большим, что все особые точки 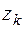 функции
функции 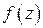 , лежащие в верхней полуплоскости, попадают внутрь указанного полукруга (рис.6).
, лежащие в верхней полуплоскости, попадают внутрь указанного полукруга (рис.6).
Рис.6
В силу основной теоремы о вычетах
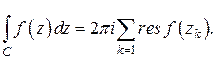 (4)
(4)
3) представляем интеграл (4) как сумму
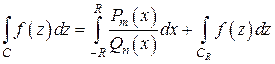 (5)
(5)
и переходим к пределу при 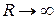 . Из условия
. Из условия 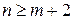 следует, что функция
следует, что функция 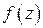 в окрестности бесконечно удаленной точки имеет нуль порядка не ниже второго, значит, может быть представлена в виде
в окрестности бесконечно удаленной точки имеет нуль порядка не ниже второго, значит, может быть представлена в виде 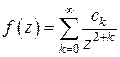 . Поэтому для второго слагаемого имеет место оценка
. Поэтому для второго слагаемого имеет место оценка
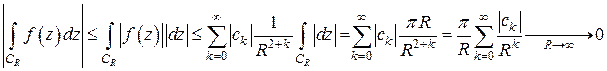
В результате предельного перехода  в формуле (5) остается только первое слагаемое, равное искомому интегралу.
в формуле (5) остается только первое слагаемое, равное искомому интегралу.
4) вычисляем интеграл (3) по формуле
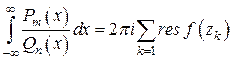 . (6)
. (6)
Здесь 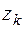 – особые точки функции
– особые точки функции 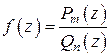 , лежащие в верхней полуплоскости, т.е.
, лежащие в верхней полуплоскости, т.е. 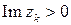 .
.
Пример 2. Вычислить интеграл 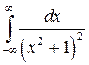 .
.
Решение. Здесь 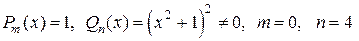 , значит, можно действовать по приведенной схеме. Строим аналитическое продолжение подынтегральной функции:
, значит, можно действовать по приведенной схеме. Строим аналитическое продолжение подынтегральной функции: 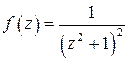 . Из двух особых точек
. Из двух особых точек 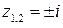 этой функции только точка
этой функции только точка 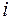 расположена в верхней полуплоскости. По формуле (6)
расположена в верхней полуплоскости. По формуле (6) 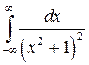
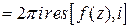 . В точке
. В точке 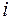 функция
функция 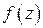 имеет полюс 2-го порядка:
имеет полюс 2-го порядка:
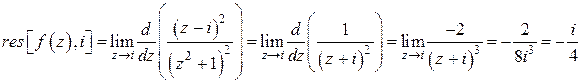 .
.
Значит, 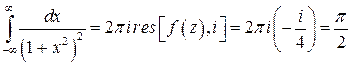 .
.
Заметим, что при вычислении этого интеграла методами математического анализа пришлось бы использовать рекуррентное соотношение, сводящее интеграл 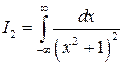 к интегралу
к интегралу 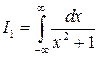 . ☻
. ☻
|
|
|
Задача 2. Показать, что 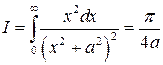
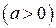 .
.
Указание. Четность подынтегральной функции позволяет записать
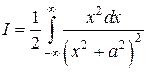 .
.
3. Интегралы вида
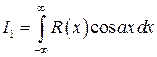 ,
, 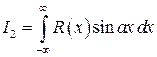 ,
,
где 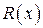 – правильная рациональная дробь;
– правильная рациональная дробь; 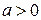 – любое вещественное число.
– любое вещественное число.
3а. Если функция 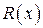 непрерывна на оси абсцисс, то вычисление таких интегралов производится по следующей схеме.
непрерывна на оси абсцисс, то вычисление таких интегралов производится по следующей схеме.
1) Вводим функцию 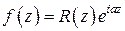 ;
;
2) Принимаем в качестве контура интегрирования, как и в предыдущем случае, 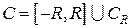 и применяем теорему о вычетах:
и применяем теорему о вычетах:
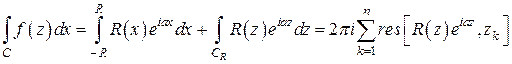 .
.
3) Переходим к пределу при 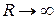 . Оценку интеграла
. Оценку интеграла 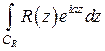 позволяет сделать
позволяет сделать
Лемма Жордана. Пусть 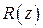 – функция, аналитическая в верхней полуплоскости, за исключением конечного числа особых точек
– функция, аналитическая в верхней полуплоскости, за исключением конечного числа особых точек 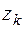 , и
, и 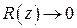 при
при 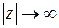 ,
, 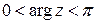 . Тогда при
. Тогда при 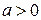
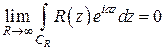 .
.
4) Значит,
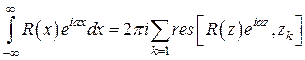 , (7)
, (7)
здесь 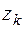 – полюсы функции
– полюсы функции 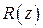 (это и полюсы функции
(это и полюсы функции 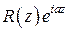 ),
), 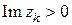 .
.
5) Формула Эйлера 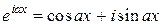 позволяет представить интеграл в виде суммы
позволяет представить интеграл в виде суммы
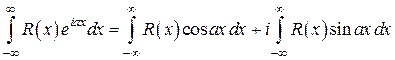 (8)
(8)
Осталось сравнить действительные и мнимые части в формулах (7) и (8). Получим искомые интегралы 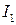 и
и 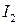 :
:
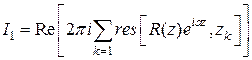
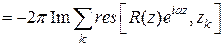 ,
,
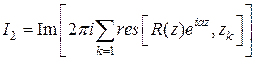
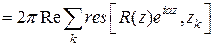 .
.
Пример 3. Вычислить интеграл 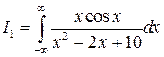 .
.
Решение. Рассмотрим функцию 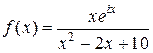 и представим ее аналитическое продолжение
и представим ее аналитическое продолжение 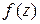 на комплексную плоскость в виде
на комплексную плоскость в виде 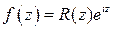 . Здесь множитель
. Здесь множитель 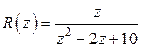 удовлетворяет условиям леммы Жордана.
удовлетворяет условиям леммы Жордана.
Особые точки функции 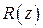 найдем из условия
найдем из условия 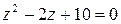 . Имеем
. Имеем 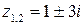 – это простые полюсы функции
– это простые полюсы функции 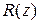 – и функции
– и функции 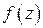 . При этом в верхней полуплоскости имеется единственная особая точка
. При этом в верхней полуплоскости имеется единственная особая точка 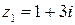 . Значит,
. Значит,
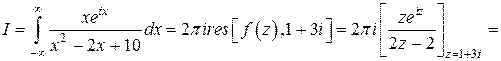
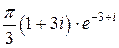
Разделяя действительную и мнимую части, получим
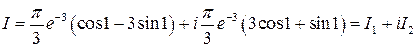
Здесь учтено, что 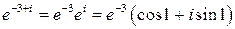 . Представим интеграл
. Представим интеграл 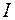 в виде суммы (8)
в виде суммы (8)
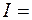
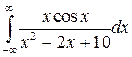
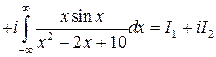
Сравнивая действительные части, получим искомый интеграл:
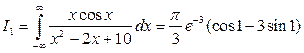 .
.
Сравнивая мнимые части, получим еще один интеграл:
 ☻
☻
Задача 3. Показать, что 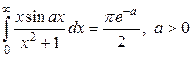 .
.
 3б. Случай, когда подынтегральная функция на действительной оси имеет простые полюсы в точках
3б. Случай, когда подынтегральная функция на действительной оси имеет простые полюсы в точках 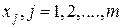 , отличается от предыдущего. Теорема о вычетах здесь применяется к контуру
, отличается от предыдущего. Теорема о вычетах здесь применяется к контуру  , показанному на рис. 7. Если на контуре
, показанному на рис. 7. Если на контуре 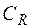 выполнены условия леммы Жордана, то получаем рис.7
выполнены условия леммы Жордана, то получаем рис.7
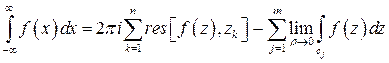 (9)
(9)
Здесь 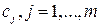 – полуокружности радиуса
– полуокружности радиуса  , охватывающие точки
, охватывающие точки 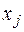 . Функция
. Функция 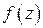 в окрестности простого полюса
в окрестности простого полюса 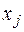 представляется в виде
представляется в виде 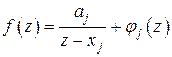 , где
, где 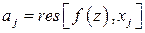 , а
, а 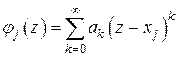 – аналити-
– аналити-
ческая в точке 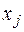 функция. Поэтому при интегрировании слагаемого
функция. Поэтому при интегрировании слагаемого 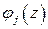 по полуокружности
по полуокружности 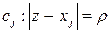 ;
; 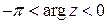 имеет место оценка
имеет место оценка
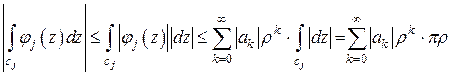 .
.
Значит, при стремлении радиуса 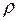 к нулю интеграл по каждой полуокружности
к нулю интеграл по каждой полуокружности 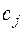 от функции
от функции 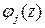 стремится к нулю. Поэтому при
стремится к нулю. Поэтому при 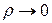 получаем
получаем
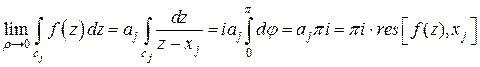 . (10)
. (10)
Остается подставить полученное выражение (10) в формулу (9):
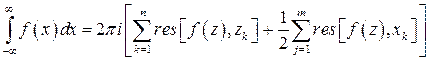 . (11)
. (11)
Здесь 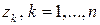 – особые точки функции
– особые точки функции 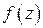 , лежащие в верхней полуплоскости (
, лежащие в верхней полуплоскости (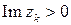 ),
), 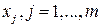 – полюсы функции
– полюсы функции 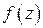 на действительной оси.
на действительной оси.
Пример 4. Вычислить интеграл 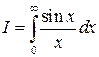
Решение. Четность подынтегральной функции и соотношение 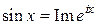 позволяют представить заданный интеграл в виде
позволяют представить заданный интеграл в виде
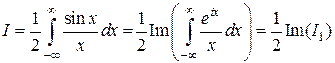 , где
, где 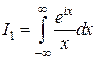 .
.
Вычислим интеграл 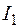 в соответствии с изложенной выше схемой. Так как у функции
в соответствии с изложенной выше схемой. Так как у функции 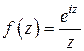 в верхней полуплоскости нет особых точек, а на действительной оси имеется простой полюс в точке
в верхней полуплоскости нет особых точек, а на действительной оси имеется простой полюс в точке 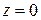 , то по формуле (11) получаем
, то по формуле (11) получаем
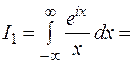
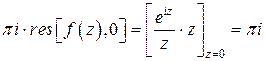 .
.
Значит, 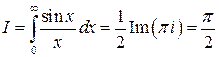 . ☻
. ☻
Задача 4. Показать, что  .
.
Пример 5. Вычислить интегралы Френеля
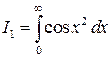 ,
, 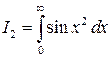 .
.
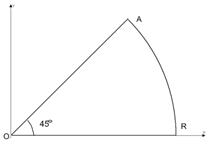
Решение. Рассмотрим функцию
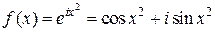
и ее аналитическое продолжение 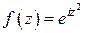 . Вычислим интеграл
. Вычислим интеграл 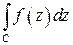 , контур интегрирования
, контур интегрирования 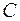 Рис.8
Рис.8
изображен на рис. 8. Внутри этого контура и на нем функция 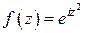 является аналитической и в силу теоремы Коши
является аналитической и в силу теоремы Коши
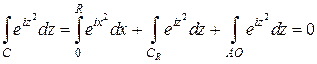 . (12)
. (12)
Выясним, что происходит с каждым из слагаемых при 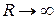 . В интеграле
. В интеграле 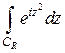 по дуге
по дуге 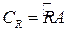 сделаем замену
сделаем замену 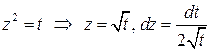 . В результате получим интеграл
. В результате получим интеграл 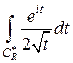 , здесь
, здесь 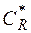 – образ дуги
– образ дуги 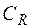 при отображении
при отображении 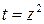 , а подынтегральная функция
, а подынтегральная функция 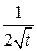 удовлетворяет условию леммы Жордана. Значит, при
удовлетворяет условию леммы Жордана. Значит, при 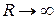 получаем
получаем 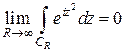 .
.
На отрезке 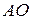 :
: 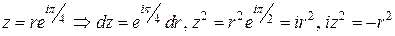 . Значит,
. Значит, 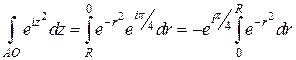 . Переходя к пределу при
. Переходя к пределу при 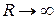 и вспоминая, что
и вспоминая, что 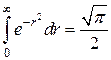 (интеграл Пуассона), получим
(интеграл Пуассона), получим 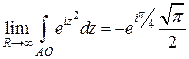
Слагаемое 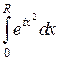 при
при 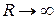 превращается в несобственный интеграл
превращается в несобственный интеграл 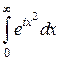 , таким образом, соотношение (12) принимает вид
, таким образом, соотношение (12) принимает вид 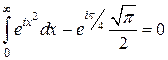 или
или
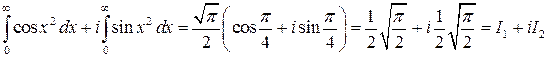 .
.
Отсюда следует: 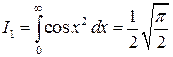
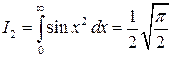 ☻
☻
Пример 6. Вычислить интеграл 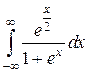 .
.
Решение. Введем функцию 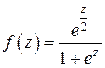 и рассмотрим интеграл
и рассмотрим интеграл 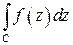 ,
,
где контур интегрирования 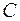 – прямоугольник с вершинами в точках
– прямоугольник с вершинами в точках 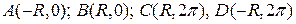 . Особые точки функции
. Особые точки функции  найдем из условия
найдем из условия 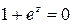
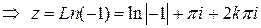 , откуда
, откуда 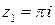 – единственный простой нуль знаменателя (простой полюс функции
– единственный простой нуль знаменателя (простой полюс функции 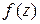 ), находящийся в полосе
), находящийся в полосе 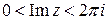 . Найдем вычет функции
. Найдем вычет функции 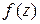 в этом полюсе:
в этом полюсе:
|
|
|
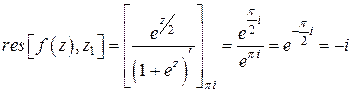 .
.
По основной теореме о вычетах
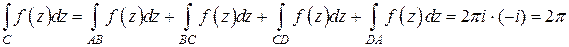 .
.
На отрезке 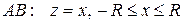 , значит,
, значит, 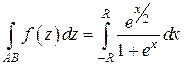 .
.
На отрезке 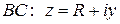 ,
,  , значит,
, значит, 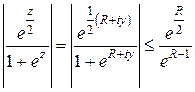
Здесь при оценке знаменателя использовано неравенство треугольника
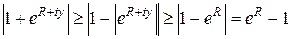 , так как
, так как  .
.
Значит,  при
при 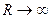 .
.
Аналогично на отрезке 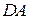 :
: 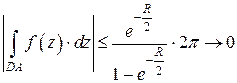 при
при  .
.
На отрезке 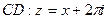 ,
, 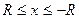 , значит,
, значит,
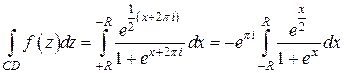
(так как 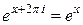 в силу периодичности функции
в силу периодичности функции 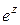 ).
).
Остается перейти к пределу при  в слагаемых
в слагаемых 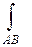 и
и 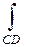 :
: 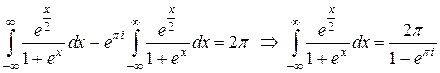 . ☻
. ☻
Задача 5. Показать, что 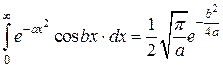 ,
, 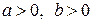
(взять 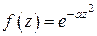 ; контур С – прямоугольник со сторонами
; контур С – прямоугольник со сторонами  и
и 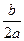 ).
).
Задания для самостоятельной работы.
Вычислить интегралы (все параметры положительны)
1. 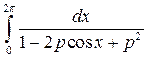 , , 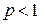 ; 2. ; 2. 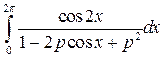 , , 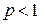 ; ;
|
3. 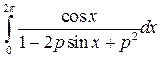 , , 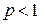 ; ;
| 4.  , , 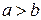 ; ;
|
5. 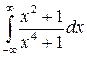
| 6. 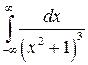 ; ;
|
7. 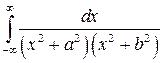 ; ;
| 8. 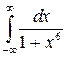
|
9. 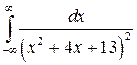 ; ;
| 10. 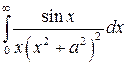 ; ;
|
11. 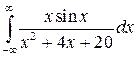 ; ;
| 12. 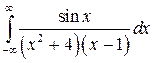
|
13. 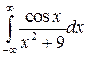 ; ;
| 14. 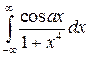 ; ;
|
15. 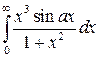 ; ;
| 16. 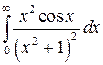 ; ;
|
17. 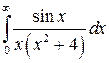 ; ;
| 18. 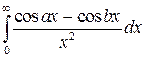 ; ;
|
Литература
1. А.И. Маркушевич. Теория аналитических функций, Гостехиздат,1960.
2. И.И.Привалов. Введение в теорию функций комплексного переменного, Наука,1967
3. Г.Л. Лунц, А.Э. Эльсгольц. Функции комплексного переменного, Наука,1958.
4. Л.И.Волковыский, Г.Л.Лунц, И.Г.Араманович., Сборник задач по теории функций комплексного переменного. Наука,1970.
5. Ю.В.Сидоров, М.В.Федорюк, М.И.Шабунин, Лекции по теории функций комплексного переменного. Наука, 1976.
6. М.А.Евграфов, Ю.В.Сидоров, М.В.Федорюк, М.И. Шабунин, К.А. Бежанов, Сборник задач по теории аналитических функций, Наука, 1969.
 2015-03-27
2015-03-27 1047
1047