Рассмотрим уравнение
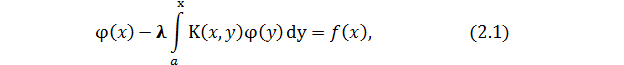
где 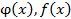 непрерывны на [a,x), а
непрерывны на [a,x), а 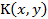 - непрерывна в основном квадрате: a≤ x, y>x.
- непрерывна в основном квадрате: a≤ x, y>x.
Будем искать решение в виде ряда

где функции 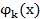 подлежат определению.
подлежат определению.
Предположим, что ряд (2.2) равномерно сходится и 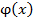 – решение уравнения (2.1), тогда (2.2)→(2.1):
– решение уравнения (2.1), тогда (2.2)→(2.1):
Подставляя предполагаемое решение (2.2) в обе части уравнения (2.1) и переставляя порядок интеграла и суммы, что в силу равномерной сходимости ряда получим.
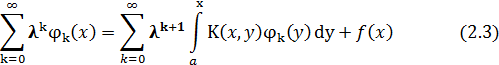
Степенные ряды, стоящие в левой и правой частях соотношения, будут совпадать тогда и только тогда, когда равны коэффициенты в степенных рядах при одинаковых степенях λ. Приравнивая эти коэффициенты, получим
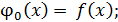
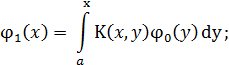
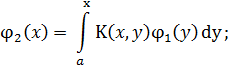
………………………………….
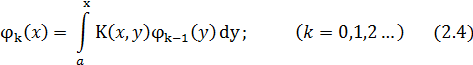
С помощью этих соотношений все коэффициенты 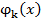 ,
, 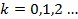 ряда (2.2) определяется однозначно, они являются непрерывными функциями на [a,b]. Подставляя (2.4) в (2.2), получим формальное решение уравнения (2.1).
ряда (2.2) определяется однозначно, они являются непрерывными функциями на [a,b]. Подставляя (2.4) в (2.2), получим формальное решение уравнения (2.1).
Покажем, что ряд (2.2) действительно равномерно сходится для всех λ. Используя ограниченность функции 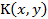 и
и 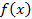 :
:
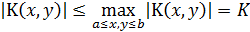
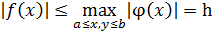
Найдем последовательно из (2.4)
|
|
|
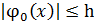
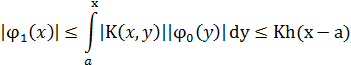
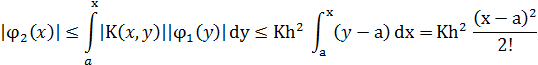
………………………………………………………………………..
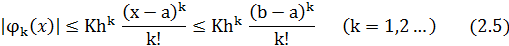
Значит ряд (2.2) мажорируется рядом
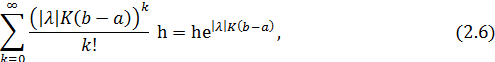
По признаку Даламбера:
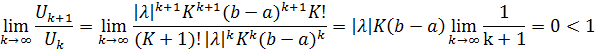
Следовательно, ряд (2.2) сходится равномерно (и абсолютно) для всех полученных 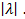 Сумма ряда
Сумма ряда 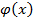 является непрерывной функцией и удовлетворяет уравнению (2.1)
является непрерывной функцией и удовлетворяет уравнению (2.1)
Итак, уравнение Вольтерра разрешимо при любом λ.
Замечания: Приведенный метод – метод последовательных подстановок – был развит Нейманом, Лиувиллем и Вольтерра. Этот метод дает решение в виде степенного ряда относительно λ, причем коэффициенты при различных степенях λ являются функциями от х. Для уравнений Вольтерра ряд сходится при всех λ. Этот метод называют еще «методом малого параметра».
Покажем теперь, что уравнение Вольтерра не может иметь более одного решения в классе ограниченных функций, ни при каком значении 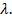
Пусть y(x) и y*(x) – два ограниченных решения уравнения, тогда разность ω(x)=y(x)-y*(x) ограничена:
Если только 
И удовлетворяет однородному уравнению
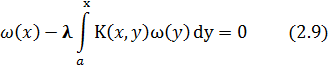
Имеем
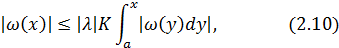
где 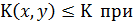
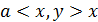
Подставляя в правую часть (2.10) вместо 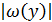 значение
значение 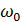 , получим в силу (2.8) новую оценку для
, получим в силу (2.8) новую оценку для 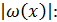
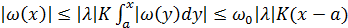 (2.11)
(2.11)
Заменяя в интеграле 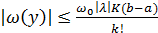 , получим
, получим
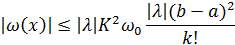
т.д.
После «k» шагов:
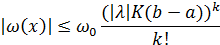
Но так как из(2.5) заключили, что ряд (2.2) мажорируется,сходящимся рядом (2.6) при всех конечных 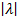 и, следовательно,
и, следовательно, 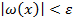 , где
, где 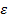 >0 – любое число, значит,
>0 – любое число, значит, 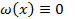 и y(x)=y*(x).
и y(x)=y*(x).
Замечание:
Значит, однородное уравнение типа Вольтерра имеет лишь тривиальное решение. Следовательно, уравнение типа Вольтерра не имеет характеристических чисел.
Найдем решение путем последовательных приближении. Выбираем 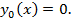 Последующие приближения определяем по формуле
Последующие приближения определяем по формуле
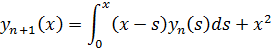
Пример. Решить уравнение
|
|
|
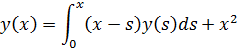
Находим
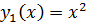
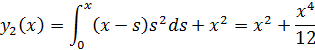
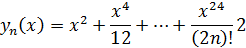
Отсюда 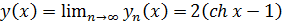
Задания для самостоятельной работы
Методом последовательных приближений решить следующие интегральные уравнения Вольтера:
1. 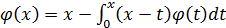 ,
, 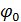 (x)=0
(x)=0
< 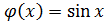 >
>
2. 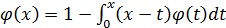 ,
, 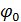 (x)=0
(x)=0
< 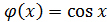 >
>
3. 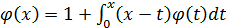 ,
, 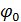 (x)=1
(x)=1
< 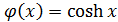 >
>
4. 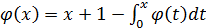 ,
, 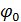 (x)=1
(x)=1
< 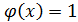 >
>
5. 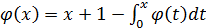 ,
, 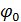 (x)=x+1
(x)=x+1
< 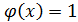 >
>
6. 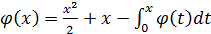 ,
, 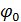 (x)=x
(x)=x
< 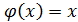 >
>
 2015-03-08
2015-03-08 1231
1231








