1.3.1. Введём три взаимно перпендикулярные прямые, пересекающиеся в одной точке, и введём на каждой из них системы координат, взяв за начало на каждой из них их общую точку пересечения О и взяв на каждой из них один и тот же масштаб. Как правило, одна ось берётся вертикальной с направлением снизу вверх, а другие две - на горизонтальной плоскости с направлениями так, как это показано на рис. 1.7.
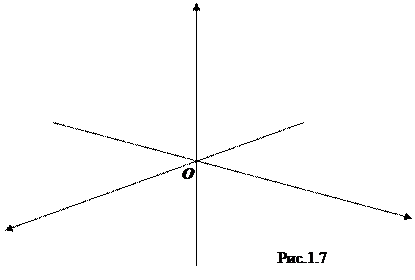
Горизонтальные оси обозначим через Ox, Оу (так, как это изображено на рис. 1.8) и назовём их соответственно осями абсциис и ординат, а вертикальную - через Oz и назовём её осью аппликат. Плоскости, содержащие пары координатных осей, называются координатными плоскостями. Они обозначаются в соответствии с тем, какие оси содержат: xOy, xOz, yOz. Тройка (Ox, Oу, Oz) называется прямоугольной декартовой системой координат в пространстве.
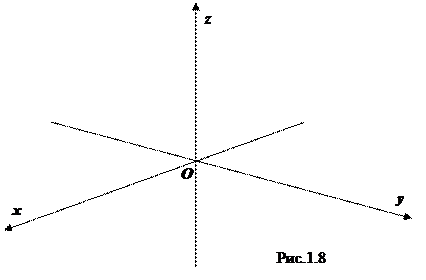
Возьмём в пространстве произвольную точку А и проведём через неё плоскости, перпендикулярные к осям Ox, Oy и Oz. Эти плоскости пересекают оси в некоторых точках. Обозначим их соответственно через Ax, Ay и Az. Они имеют на осях какие-то координаты, скажем, xA, yA и zA. Таким образом, Ax (xA), Ay (yA) и Az (zA) - основания перпендикулярных к осям плоскостей, проведённых из точки А (рис. 1.9).
Тройка чисел (xA, yA, zA) называется координатами точки А, при этом xA - абсцисса точки А, yA - ордината точки А, zA - аппликата точки А. Тот факт, что точка А имеет координаты (xA, yA, zA), обозначается через А (xA, yA, zA).

 При изображении положения точки А (xA, yA, zA) относительно своих координат проводят проекцию A ¢ точки A на координатную плоскость xOy, затем проводят отрезки A ¢ Ax, A ¢ Ay, параллельные соответственно осям Oy, Ox, и отрезок AAz, параллельный отрезку A ¢ O (рис.1.10, здесь точки Ax, Ay, Az обозначены их координатами, соответственно через xA, yA, zA).
При изображении положения точки А (xA, yA, zA) относительно своих координат проводят проекцию A ¢ точки A на координатную плоскость xOy, затем проводят отрезки A ¢ Ax, A ¢ Ay, параллельные соответственно осям Oy, Ox, и отрезок AAz, параллельный отрезку A ¢ O (рис.1.10, здесь точки Ax, Ay, Az обозначены их координатами, соответственно через xA, yA, zA).
1.3.2. Теорема. Если точки A (xA, yA, zA) и B (xB, yB, zB) заданы своими координатами, то расстояние между ними равно
| АВ |= 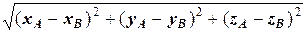 ,
,
и если точка C (xC, yC, zC) делит отрезок АВ в отношении l, то xC = 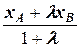 , yC =
, yC = 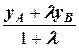 , zC =
, zC = 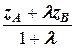 .
.
1.3.3. Упражнение. Даны точки A и B своими координатами. Известно, что точка C делит отрезок AB в отношении l. Найти длину отрезка AB и координаты точки C. В системе координат изобразить отрезок AB:
а) A (-2; 3; 4), B (4; 2; -3), l = 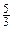 ;
;
б) A (3; -2; 1), B (-4; 2; 0), l = 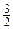 ;
;
в) A (2; -4; 3), B (4; -2; 2), l =3.
Решение. а) По теореме 1.3.2 имеем
| АВ |= 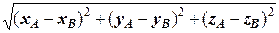 =
= 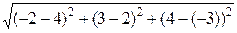 =
= 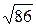 ,
,
По той же теореме
xC = 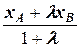 =
= 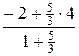 =
= 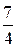 , yC =
, yC = 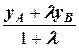 =
= 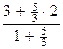 =
= 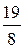 , zC =
, zC = 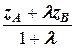 =
= 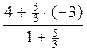 = -
= - 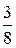
то есть 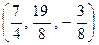 - координаты точки С.
- координаты точки С.
В системе координат изобразим отрезок AB:

Ответ: | АВ |= 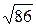 ,
, 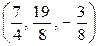 - координаты точки С.
- координаты точки С.
 2015-03-08
2015-03-08 1380
1380








